
47. (1)B(-1,0),C(4,0),由题意,得
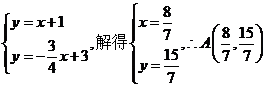
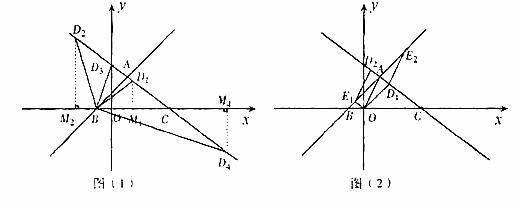
(2)当 为等腰三角形时,有以下三种情形,如图(1)。设动点D的坐标为(x,y),由(1),得B(-1,0),C(4,0),故BC=5。
为等腰三角形时,有以下三种情形,如图(1)。设动点D的坐标为(x,y),由(1),得B(-1,0),C(4,0),故BC=5。
当 时,过点
时,过点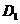 作
作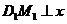 轴,垂足为点
轴,垂足为点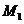 ,则
,则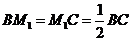 。
。
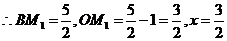 。
。
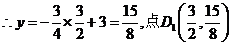 。
。
②当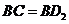 时,过点
时,过点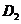 作
作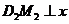 轴,垂足为点
轴,垂足为点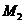 ,则
,则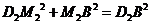 。
。
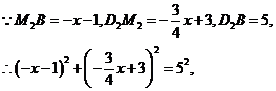
解,得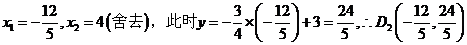 。
。
③当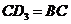 ,或
,或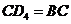 时,同理得
时,同理得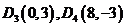 。
。
故点D坐标分别为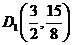 ,
,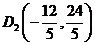 ,
,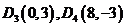 。
。
(3)存在。以点E,D,O,A为顶点的四边形是平行四边形有以下三种情形,如图(2)。
①当四边形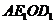 为平行四边形时,
为平行四边形时,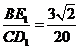 。
。
②当四边形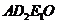 为平行四边形时,
为平行四边形时,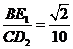 。
。
当四边形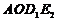 为平行四边形时,
为平行四边形时,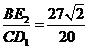 。
。
46. 解:(1)方法一:由已知得:C(0,-3),A(-1,0)
将A、B、C三点的坐标代入得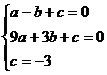
解得: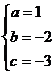
所以这个二次函数的表达式为: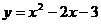
方法二:由已知得:C(0,-3),A(-1,0)
设该表达式为: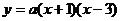
将C点的坐标代入得: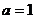
所以这个二次函数的表达式为: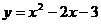
(注:表达式的最终结果用三种形式中的任一种都不扣分)
(2)方法一:存在,F点的坐标为(2,-3)
理由:易得D(1,-4),所以直线CD的解析式为: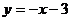
∴E点的坐标为(-3,0)
由A、C、E、F四点的坐标得:AE=CF=2,AE∥CF
∴以A、C、E、F为顶点的四边形为平行四边形
∴存在点F,坐标为(2,-3)
方法二:易得D(1,-4),所以直线CD的解析式为: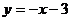
∴E点的坐标为(-3,0)
∵以A、C、E、F为顶点的四边形为平行四边形
∴F点的坐标为(2,-3)或(―2,―3)或(-4,3)
代入抛物线的表达式检验,只有(2,-3)符合
∴存在点F,坐标为(2,-3)
(3)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
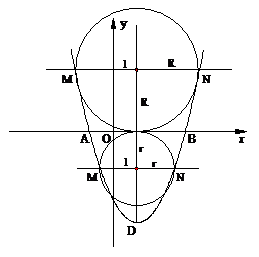 代入抛物线的表达式,解得
代入抛物线的表达式,解得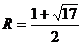
②当直线MN在x轴下方时,设圆的半径为r(r>0),
则N(r+1,-r),
代入抛物线的表达式,解得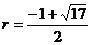
∴圆的半径为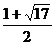 或
或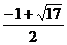 .
.
(4)过点P作y轴的平行线与AG交于点Q,
易得G(2,-3),直线AG为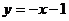 .
.
设P(x,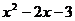 ),则Q(x,-x-1),PQ
),则Q(x,-x-1),PQ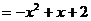 .
.
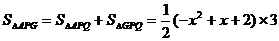
当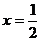 时,△APG的面积最大
时,△APG的面积最大
此时P点的坐标为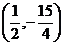 ,
, .
.
45.
44.
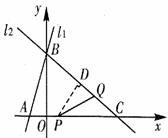
(1)由题意,知B(0,6),C(8,0)
设直线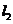 的解析式为
的解析式为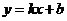 ,则
,则
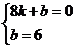 ,解得
,解得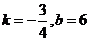
则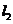 的解析式为
的解析式为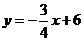 。
。
(2)解法一:如图,过P作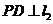 于D,则
于D,则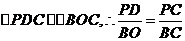
由题意,知OA=2,OB=6,OC=8
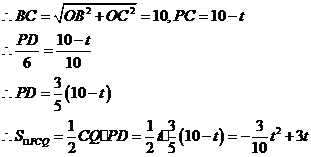
解法二:如图,过Q作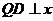 轴于D,则
轴于D,则
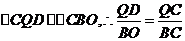
由题意,知OA=2,OB=6,OC=8
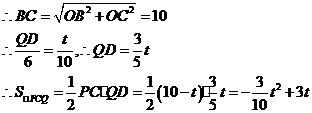
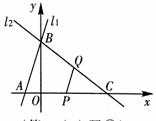
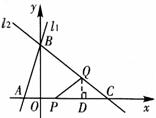
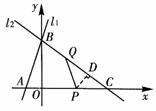
(3)要想使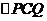 为等腰三角形,需满足CP=CQ,或QC=QP,或PC=PQ。
为等腰三角形,需满足CP=CQ,或QC=QP,或PC=PQ。
①当CP=CQ时(如图①),得10-t=t。解,得t=5。
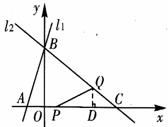
②当QC=QP时(如图②),过Q作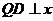 轴于D,则
轴于D,则
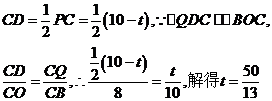
③当PC=PQ时(如图③),过P作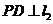 于D,则
于D,则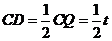
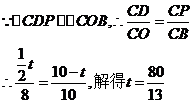
综上所述,当t=5,或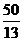 ,或
,或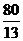 时,
时,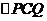 为等腰三角形。
为等腰三角形。
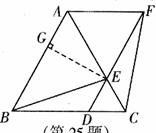
43.
(1)(选证一)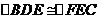
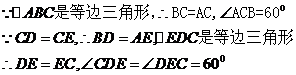
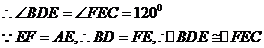
(选证二)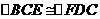
证明: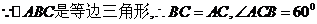
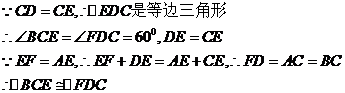
(选证三)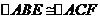
证明: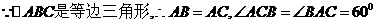
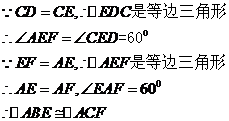
(2)四边形ABDF是平行四边形。
由(1)知,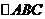 、
、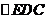 、
、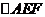 都是等边三角形。
都是等边三角形。
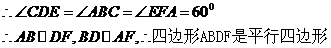
(3)由(2)知,)四边形ABDF是平行四边形。
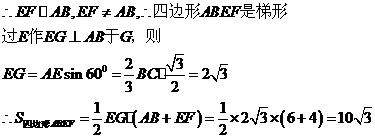
42.
(1)设抛物线解析式为y=a(x-1)(x+3)…………………………1分
(只要设出解析式正确,不管是什么形式给1分)
将(0,-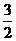 )代入,解得a=
)代入,解得a=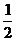 .
.
∴抛物线解析式为y=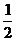 x2+x-
x2+x-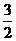 …………………………………3分
…………………………………3分
(无论解析式是什么形式只要正确都得分)
画图(略)。(没有列表不扣分)…………………………………5分
(2)正确的画出反比例函数在第一象限内的图像……………7分
由图像可知,交点的横坐标x0 落在1和2之间,从而得出这两个相邻的正整数为1与2。…………………………………………………9分
(3)由函数图像或函数性质可知:当2<x<3时,
对y1=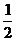 x2+x-
x2+x-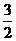 , y1随着x增大而增大,对y2=
, y1随着x增大而增大,对y2=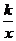 (k>0),
(k>0),
y2随着X的增大而减小。因为A(X0,Y0)为二次函数图像与反比例函数图像的交点,所心当X0=2时,由反比例函数图象在二次函数上方得y2>y1,
即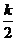 >
>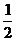 ×22+2-
×22+2-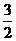 ,解得K>5。…………………………………11分
,解得K>5。…………………………………11分
同理,当X0=3时,由二次函数数图象在反比例上方得y1>y2,
即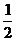 ×32+3-
×32+3-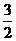 >
>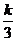 ,解得K<18。…………………………………13
,解得K<18。…………………………………13
所以K的取值范围为5 <K<18………………………………………14分
说明:
所有解答题都只给出了一种解法,如有其它解法可参照以上标准给分。
解题过程中,若某一步数据使用错了,但思路正确,且按错误数据计算到“正确”结果,则给由此向下相应得分的二分之一。
41.(1)1.9 …………………………………………………2分
(2) 设直线EF的解析式为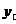 乙=kx+b
乙=kx+b
∵点E(1.25,0)、点F(7.25,480)均在直线EF上
∴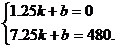 ………………………………………………3分
………………………………………………3分
解得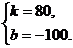 ∴直线EF的解析式是y乙=80X-100……………4分
∴直线EF的解析式是y乙=80X-100……………4分
∵点C在直线EF上,且点C的横坐标为6,
∴点C的纵坐标为80×6-100=380
∴点C的坐标是(6,380)………………………………………5分
设直线BD的解析式为y甲 = mx+n
∵点C(6,380)、点D(7,480)在直线BD上
∴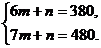 …………………………………………………6分
…………………………………………………6分
解得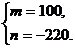 ∴BD的解析式是y甲=100X -220 ……………7分
∴BD的解析式是y甲=100X -220 ……………7分
∵B点在直线BD上且点B的横坐标为4.9,代入y甲得B(4.9,270)
∴甲组在排除故障时,距出发点的路程是270千米。……………8分
(3)符合约定
由图像可知:甲、乙两组第一次相遇后在B和D相距最远。
在点B处有y乙-y甲=80×4.9-100-(100×4.9-220)=22千米<25千米
…………………………10分
在点D有y甲-y乙=100×7-220-(80×7-100)=20千米<25千米
…………………………11分
∴按图像所表示的走法符合约定。………………………………12分
40. 解:(1)连结AD,则∠ADO=∠B=600
在Rt△ADO中,∠ADO=600
所以OD=OA÷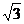 =3÷
=3÷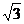 =
=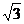
|
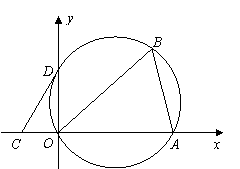 所以D点的坐标是(0,
所以D点的坐标是(0,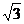 )
)
 (2)猜想是CD与圆相切
(2)猜想是CD与圆相切
∵ ∠AOD是直角,所以AD是圆的直径
|
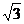 =
=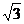 , ∠CDO=300
, ∠CDO=300
∴∠CDA=∠CDO+∠ADO=Rt∠ 即CD⊥AD
∴ CD切外接圆于点D
(3)依题意可设二次函数的解析式为 :
y=α(x-0)(x-3)
由此得顶点坐标的横坐标为:x=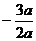 =
=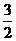 ;
;
即顶点在OA的垂直平分线上,作OA的垂直平分线EF,则得∠EFA=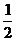 ∠B=300
∠B=300
得到EF=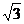 EA=
EA=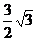 可得一个顶点坐标为(
可得一个顶点坐标为(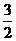 ,
,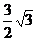 )
)
同理可得另一个顶点坐标为(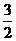 ,
,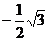 )
)
分别将两顶点代入y=α(x-0)(x-3)可解得α的值分别为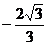 ,
,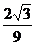
则得到二次函数的解析式是y=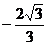 x(x-3)或y=
x(x-3)或y=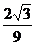 x(x-3)
x(x-3)
39. 解:(1)由题意得: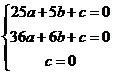 2分
2分
解得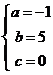 3分
3分
故抛物线的函数关系式为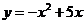 4分
4分
(2)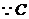 在抛物线上,
在抛物线上,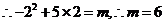 5分
5分
 点坐标为(2,6),
点坐标为(2,6), 、C在直线
、C在直线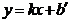 上
上

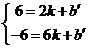 解得
解得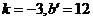
 直线BC的解析式为
直线BC的解析式为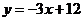 6分
6分
设BC与x轴交于点G,则G的坐标为(4,0)
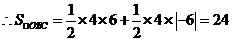 7分
7分
(3)存在P,使得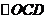 ∽
∽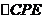 8分
8分
设P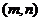 ,
,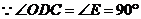
故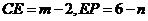
若要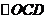 ∽
∽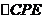 ,则要
,则要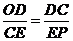 或
或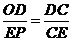
即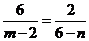 或
或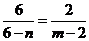
解得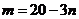 或
或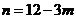
又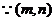 在抛物线上,
在抛物线上,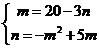 或
或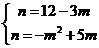
解得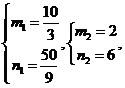 或
或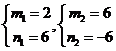
故P点坐标为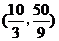 和
和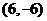 10分
10分
(只写出一个点的坐标记9分)
38. 解:(1) ∵以AB为直径作⊙O′,交y轴的负半轴于点C,
∴∠OCA+∠OCB=90°,
又∵∠OCB+∠OBC=90°,
∴∠OCA=∠OBC,
又∵∠AOC= ∠COB=90°,
∴ΔAOC∽ ΔCOB, 1分
∴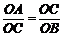 .
.
又∵A(–1,0),B(9,0),
∴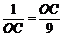 ,解得OC=3(负值舍去).
,解得OC=3(负值舍去).
∴C(0,–3),
3分
设抛物线解析式为y=a(x+1)(x–9),
∴–3=a(0+1)(0–9),解得a=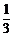 ,
,
∴二次函数的解析式为y=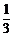 (x+1)(x–9),即y=
(x+1)(x–9),即y=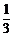 x2–
x2–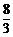 x–3. 4分
x–3. 4分
(2) ∵AB为O′的直径,且A(–1,0),B(9,0),
∴OO′=4,O′(4,0), 5分
∵点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,
∴∠BCD=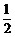 ∠BCE=
∠BCE=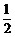 ×90°=45°,
×90°=45°,
连结O′D交BC于点M,则∠BO′D=2∠BCD=2×45°=90°,OO′=4,O′D=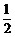 AB=5.
AB=5.
∴D(4,–5). 6分
∴设直线BD的解析式为y=kx+b(k≠0)
∴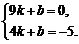 7分
7分
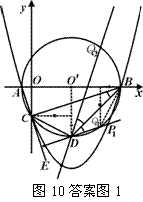 解得
解得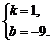
∴直线BD的解析式为y=x–9. 8分
(3) 假设在抛物线上存在点P,使得∠PDB=∠CBD,
解法一:设射线DP交⊙O′于点Q,则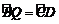 .
.
分两种情况(如答案图1所示):
①∵O′(4,0),D(4,–5),B(9,0),C(0,–3).
∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,
因此,点Q1(7,–4)符合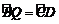 ,
,
∵D(4,–5),Q1(7,–4),
∴用待定系数法可求出直线DQ1解析式为y=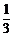 x–
x–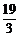 . 9分
. 9分
解方程组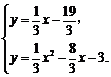 得
得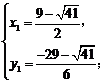
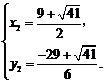
∴点P1坐标为(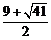 ,
,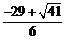 ),[坐标为(
),[坐标为(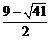 ,
,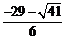 )不符合题意,舍去].
)不符合题意,舍去].
10分
②∵Q1(7,–4),
∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合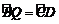 .
.
∵D(4,–5),Q2(7,4).
∴用待定系数法可求出直线DQ2解析式为y=3x–17. 11分
解方程组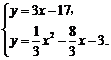 得
得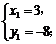
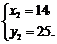
∴点P2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去].
12分
∴符合条件的点P有两个:P1(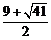 ,
,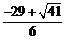 ),P2(14,25).
),P2(14,25).
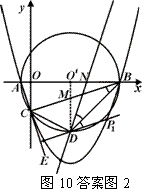 解法二:分两种情况(如答案图2所示):
解法二:分两种情况(如答案图2所示):
①当DP1∥CB时,能使∠PDB=∠CBD.
∵B(9,0),C(0,–3).
∴用待定系数法可求出直线BC解析式为y=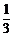 x–3.
x–3.
又∵DP1∥CB,∴设直线DP1的解析式为y=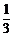 x+n.
x+n.
把D(4,–5)代入可求n= –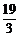 ,
,
∴直线DP1解析式为y=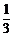 x–
x–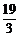 . 9分
. 9分
解方程组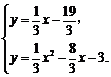 得
得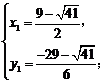
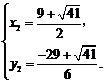
∴点P1坐标为(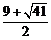 ,
,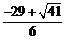 ),[坐标为(
),[坐标为(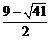 ,
,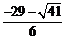 )不符合题意,舍去].
)不符合题意,舍去].
10分
②在线段O′B上取一点N,使BN=DM时,得ΔNBD≌ΔMDB(SAS),∴∠NDB=∠CBD.
由①知,直线BC解析式为y=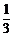 x–3.
x–3.
取x=4,得y= –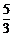 ,∴M(4,–
,∴M(4,–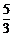 ),∴O′N=O′M=
),∴O′N=O′M=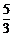 ,∴N(
,∴N(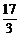 ,0),
,0),
又∵D(4,–5),
∴直线DN解析式为y=3x–17. 11分
解方程组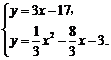 得
得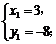
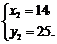
∴点P2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去].
12分
∴符合条件的点P有两个:P1(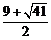 ,
,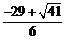 ),P2(14,25).
),P2(14,25).
解法三:分两种情况(如答案图3所示):
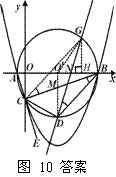 ①求点P1坐标同解法二. 10分
①求点P1坐标同解法二. 10分
②过C点作BD的平行线,交圆O′于G,
此时,∠GDB=∠GCB=∠CBD.
由(2)题知直线BD的解析式为y=x–9,
又∵ C(0,–3)
∴可求得CG的解析式为y=x–3,
设G(m,m–3),作GH⊥x轴交与x轴与H,
连结O′G,在Rt△O′GH中,利用勾股定理可得,m=7,
由D(4,–5)与G(7,4)可得,
DG的解析式为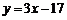 , 11分
, 11分
解方程组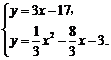 得
得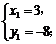
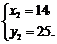
∴点P2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去]. 12分
∴符合条件的点P有两个:P1(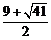 ,
,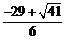 ),P2(14,25).
),P2(14,25).
说明:本题解法较多,如有不同的正确解法,请按此步骤给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com