2、指数不等式、对数不等式要注意对底数的讨论，对数不等式还要注意真要大于0。

1、　 无理不等式：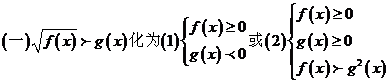

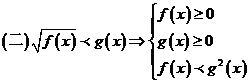
常用放缩技巧：　　　　　　　 ，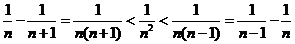

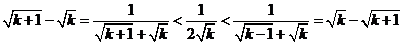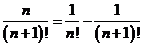
(6)利用函数的单调性(本质仍然是放缩法)，(7)反证法(对于“至多”“至少”问题、存在性问题、否定形式的命题等，总之“正难则反”)，(8)换元法(形如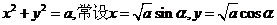：)，(9)判别式法(二次式的含参数问题常运用判别式)

算术平均数与几何平均数常用公式及变形：(1)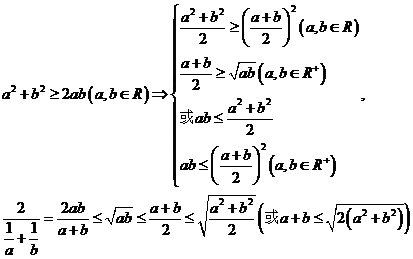

(2)

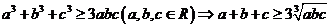
注、对于两个正数x,y，若已知xy,x+y,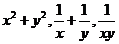中的某一个为定值，可求出其余各个的最值，如：(1)当xy＝P(定值)，那么当x=y时，和x+y有最小值2，

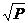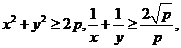
(2)x+y=S(定值)，那么当x=y时，积xy有最大值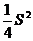

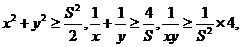
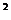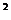(3)已知x+y=p,则x+y有最大值为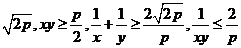

应用基本的不等式解题时，注意创设一个应用基本不等式的情境及使等号成立的条件，即“一正、二定、三相等”

1.)同向不等式可以相加；异向不等式可以相减：a＞b,c＞d ，则 a+c＞b+d,　(a>b ,c<d　 则a－c>b－d)，但异向不等式不可以相加；同向不等式不可以相减(2)左右同正不等式：同向的不等式可以相乘但不能相除；异向不等式可以相除但不能相乘：a>b>0　c>d>0 (a>b, c<d)　 ，　 则ac>bd(或)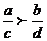

(3)左右同正不等式：两边可以同时乘方或开方 a>b>0则a>b或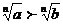　

(4)ab>0,则a>b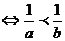,(ab<0　则a>b)

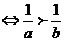4、正弦定理在解三角形中的应用：(1)已知两角和一边解三角形，只有一解。

(2)已知两边和其中一边的对角，解三角形，要注意对解的个数的讨论。可按如下步骤和方法进行：先看已知角的性质和已知两边的大小关系。如已知a,b,A.(一)若A为钝角或直角，当b≥a时，则无解。当a≥b时，有只有一个解。(二)若A为锐角，结合下图理解。1)若a≥b或a=bsinA,则只有一个解。2)若bsinA＜a＜b,则有两解。3)若a＜bsinA,则无解。

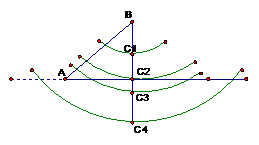
　　　　　　也可根据a,b的关系及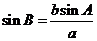与1的大小关系来确定。

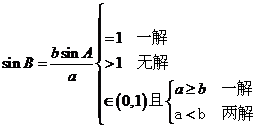
如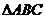：中，A、B的对边分别是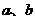，且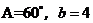，那么满足条件的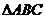，(1)只有一个解时，边长a的取值范围是＿＿＿＿＿＿＿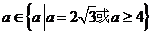

(2)有两解时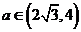，，(3)无解时，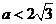

余弦定理在解三角形中的应用：(1)已知两边和夹角，(2)已知三边。

第十七讲不等式

3、其它公式：

(1)　　　　　 射影公式：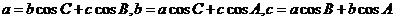

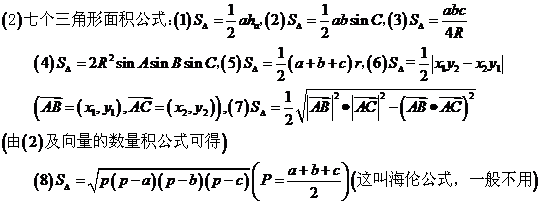
其中r为三角形ABC内切圆半径，R为外接圆的半径，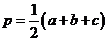

2、余弦定理：在三角形ABC中，有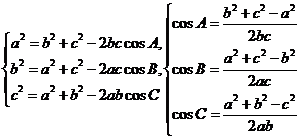

1、正弦定理：在三角形ABC中，a,b,c分别为角A，B，C的对边，R为三角形ABC的外接圆的半径，则有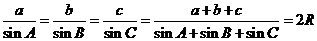，注意以下一些变式：

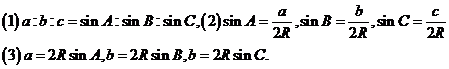
17、平移公式：将点P(x,y),按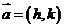平移至点P′(xˊ,yˊ),

则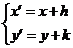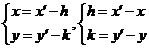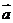，，叫平移向量。

图象的平移：设函数y=f(x)的图象为C，将C上每一点均按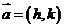平移，得一个新的图象C′，则C′对应的函数关系式为y-k=f(x-h),即y=f(x-h)+k,

(2)函数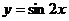的图象按向量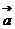平移后，所得函数的解析式是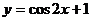，则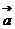＝________(答：)

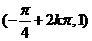第十六讲正弦定理与余弦定理