
(三)重点、难点的学习与目标完成过程
1.请学生观察“正切和余切表”的结构,并用语言加以概括.
答:正切表在76°-90°无修正值,余切表在0°-14°无修正值.其余与正弦和余弦表类似,对于正切值,随角度的增大而增大,随角度的减小而减小,而余切值随角度的增大而减小,随角度的减小而增大.
2.查表示范.
例2 查表求下列正切值或余切值.
(1)tan53°49′; (2)cot14°32′.
学生有查“正弦和余弦表”的经验,又了解了“正切和余切表”的结构,完全可自行查表.在学生得出答案后,请一名学生讲解“我是怎样查表的”,教师板书:
解:(1)tan53°48′=1.3663
角度增1′值减0.0008.
tan53°49′=1.3671;
(2)cot14°30′=3.867
角度增2′值增0.009.
cot14°30′=3.858.
在讲解示范例题后,应请学生作一小结:查锐角的正切值类似于查正弦值,应“顺”着查,若使用修正值,则角度增加时,相应的正切值要增加,反之,角度减小时,相应的正切值也减小;查余切表与查余弦表类似,“倒”着查,在使用修正值时,角度增加,就相应地减去修正值,反之,角度减小,就相应地加上修正值.
为了使学生熟练地运用“正切和余切表”,已知锐角查其正切、余切值,书上配备了练习题1,查表求下列正切值和余切值:
(1)tan30°12′,tan40°55′,tan54°28′,tan74°3′;
(2)cot72°18′,cot56°56′,cot32°23′,cot15°15′.
在这里让学生加以练习.
例3 已知下列正切值或余切值,求锐角A.
(1)tanA=1.4036; (2)cotA=0.8637.
因为学生已了解由正弦(余弦)值求锐角的方法,由其正迁移,不难发现由正切值或余切值求锐角的方法.所以例3出示之后,应请学生先探索查表方法,试查锐角A的度数,如有疑问,教师再作解释.
解:(1)1.4019=tan54°30′
值增0.0017 角度增2′
1.4036=tan54°32′.
∴锐角A=54°32′.
(2)0.8632=cot49°12′.
值增0.0005 角度减1′
0.8637=cot49°11′.
∴锐角A=49°11′.
已知锐角的正切值或余切值,查表求锐角对学生来说比已知锐角查表求值要难,因此在解完例题之后还应引导学生加以小结.
教材为例3配备了练习2,已知下列正切值或余切值,求锐角A或B.
(1)tanB=0.9131,tanA=0.3314,
tanA=2.220,tanB=31.80;
(2)cotA=1.6003,cotB=3.590,
cotB=0.0781,cotA=180.9.
学生在独立完成此练习之后,教师应组织学生互评,使学生在交流中互相帮助.
(二)整体感知
学生在第一大节曾查过“正弦和余弦表”,知道为什么正、余弦用同一份表格,并了解在0°-90°之间正、余弦值随角度变化的情况,会正确地使用修正值.
本节课在第一大节基础上安排查“正切和余切表”,学生不会感到困难.只是正切表在76°-90°无修正值,余切表在0°-14°无修正值,这一点与“正弦和余弦表”有所区别,教学中教师应着重强调这一部分.
 (一)明确目标
(一)明确目标
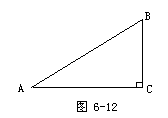
1.结合图6-12说明:什么是∠A的正切、余切?因为这是本章最重要的概念,因此要求全体学生掌握.这里不妨提问成绩较差的学生,以检查学生掌握的情况.
2.一个锐角的正切(余切)与其余角的余切(正切)之间具有什么关系?并写出表达式.
答:tanA=cot(90°-A),cotA=tan(90°-A).
3.∠A的正切值与余切值具有什么关系,请用式子表达_
答tanA=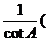 或cotA=
或cotA=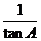 或tanA
或tanA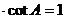
4.结合2、3中复习的内容,配备练习题加以巩固:
(1)tan35°·tan45°·tan55°=______;
(2)若tan35°·tan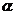 =1,则
=1,则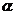 =______;
=______;
(3)若tan47°·cotβ=1,则β=______.
这几个小题学生在回答时,极易出错.因此在本课课前复习中出示它们,结合知识点的复习,便于学生加以比较.
5.提问0°、30°、45°、60°、90°五个特殊角的三角函数值各是多少?要求学生熟记.
6.对于任意锐角的正切值、余切值,我们从何得知呢?本节课,我们就来研究“正切和余切表”.
这样引入较自然.学生有查“正弦和余弦表”的经验,对查“正切和余切表”必定充满信心.
3.疑点:在使用余切表中的修正值时,如果角度增加,相应的余切值要减少一些;如果角度减小,相应的余切值要增加一些.这里取加还是取减,学生极易出错.
2.难点:使学生会查“正切和余切表”.
1.重点:使学生会查“正切和余切表”.
(三)德育渗透点
培养学生良好的学习习惯.
(二)能力训练点
逐步培养学生观察、比较、分析、概括等逻辑思维能力.
(一)知识教学点
使学生学会查“正切和余切表”.
|
14.2正切和余切(一) 一、概念 三、锐角三角函数 五、互为余角的正切与余 _____________ _________________ 切值关系 _____________ _________________ _____________________ 二、tanA与cotA关系 四、特殊角的正切与余 六、例题 ________________ 切值(幻灯片) ___________________ ________________ ___________________ ___________________ |
正切和余切(二)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com