
(一)知识教学点
使学生了解正切、余切的概念,能够正确地用tanA、cotA表示直角三角形(其中一个锐角为∠A)中两边的比,了解tanA与cotA成倒数关系,熟记30°、45°、60°角的各个三角函数值,会计算含有这三个特殊锐角的三角函数值的式子,会由一个特殊锐角的三角函数值说出这个角的度数,了解一个锐角的正切(余切)值与它的余角的余切(正切)值之间的关系.
|
14.1正弦和余弦(六) 一、正余弦概念及有关 二、例解 例11 知识 引例----------- ------------- ------------------- ---------------- ------------- ------------------- ---------------- -------------- |
正切和余切(一)
2.教材习题14.1A组.
对学有余力的学生可选作B组第1题.
1.看教材培养学生看书习惯.
(三)总结与扩展
请学生总结:我们研究了正弦、余弦的概念及余角余函数关系,会用“正弦和余弦表”查任一锐角的正弦、余弦值,并会用这些知识解决有关问题.
(二)重点、难点的学习与目标完成过程
1.本章引言中提到这样一个问题:修建某扬水站时,要沿着斜坡铺设水管.假设水管AB长为105.2米,∠A=30°6′,求坡高BC(保留四位有效数字).现在,这个问题我们能否解决呢?
这里出示引言中的问题,不仅调动学生的积极性,激发学习动机,同时体现了教学的完整性,首尾照应.
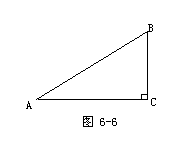
对学生来说,此题比较容易解答.教师可以请成绩较好的学生口答,
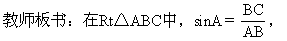
∴BC=AB·sinA
=105.2·sin30°6′
=105.2×0.5015
≈52.76(米).
这一例题不仅起到巩固锐角三角函数
概念的作用,同时为下一节“解直角三角形”做了铺垫.同时向学生渗透了数学知识来源于实践又反过来作用于实践的辩证唯物主义观点,培养学生用数学的意识.
2.为了过渡到第二大节“解直角三角形”,教材还安排了例1,它既是对概念的巩固、应用,又为解直角三角形作了铺垫.出示投影片
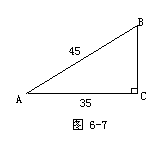
例11 如图6-7,在Rt△ABC中,已知AC=35,AB=45,求∠A(精确到1°).
分析:本题已知直角三角形的斜边长,直角边长,所以根据直角三角形中锐角的余弦定义,先求出cosA,进而查表求得∠A.
教师可请一名中等学生板书,其他学生在本上完成.
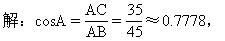
查表得∠A≈39°,
3.教材为例题配置了两个练习题,因此在完成例题后,请学生做巩固练习
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c.
(1)已知a=32,∠B=50°,求c(保留两位有效数字).
(2)已知c=20,b=14,求∠A(精确到1°).
学生在做这两个小题时,可能有几种不同解法,如(1),应选择c=

当的三角函数关系式解题,培养学生的计算能力.
4.本课安排在第一大节最后一课,因此本课还有对整个第一大节进行归纳、总结的任务.由于在课前复习中已经将几个知识点一一复习,因此这里主要配备小题对概念加以巩固和应用.
(1)判断题:
i 对于任意锐角α,都有0<sinα<1和0<cosα<1
( )
ii 对于任意锐角α1,α2,如果α1<α2,那么cosα1<cosα2 ( )
iii 如果sinα1<sinα2,那么锐角α1<锐角α2I ( )
iv 如果cosα1<cosα2,那么锐角α1>锐角α2 ( )
这道题是为巩固正弦、余弦的概念而配备的,可引导学生用图形来判断,也可用“正弦和余弦表”来判断.对于假命题,应请学生举出反例.
(2)回答下列问题
i sin20°+sin40°是否等于sin60°;
ii cos10°+cos20°是否等于cos30°.
可引导学生查表得答案.这两个小题对学生来说极易出错,因为学生对函数sinA、cosA理解得并不深,而且由于数与式的四则运算造成的负迁移,使学生易混淆.
(3)在Rt△ABC中,下列式子中不一定成立的是______
A.sinA=sinB
B.cosA=sinB
C.sinA=cosB
D.sin(A+B)=sinC
这一小题是为复习任意锐角的正弦值与余弦值的关系而设计的.通过比较几个等式,加深学生对余角余函数概念理解.
教师可请学生口答答案并说明原因.
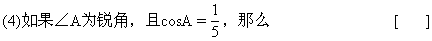
A.0°<∠A≤30°
B.30°<∠A≤45°
C.45<∠A≤60°
D.60°<∠A<90°
对于初学三角函数的学生来说,解答此题是个难点,教师应给学生充足时间讨论,这对培养学生分析问题、解决问题能力很有好处,如果学生没有思路,教师可适当点拨;要想探索∠A在哪个范围,首先观察
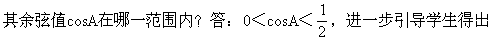 ∠A范围,答案选D.
∠A范围,答案选D.
(一)明确目标
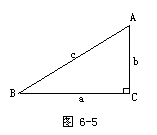
1.结合图6-5,请学生回忆,什么是∠A的正弦,余弦?教师板
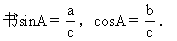
2.互余两角的正弦、余弦值之间具有什么关系?
答:sinA=cos(90°-A),cosA=sin(90°-A).
教师板书.
3.特殊角0°、30°、45°、60°、90°的正弦值余弦值各是多少?
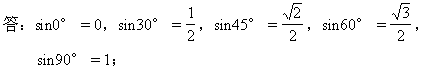
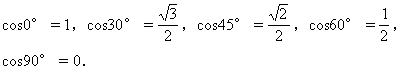
4.在0°-90°之间,锐角的正弦值、余弦值怎样随角度的变化而变化?
答:在0°-90°之间,锐角的正弦值随角度的增加(或减小)而增加(或减小);锐角的余弦值随角度的增加(或减小)而减小(或增加).
本节课我们将运用以上知识解决有关问题.
3.疑点:学生在用“正弦和余弦表”时,往往在修正值的加减上混淆不清.
2.难点:归纳总结前面的知识,并运用它们解决有关问题.
1.重点:归纳总结前面的知识,并运用它们解决有关问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com