(一)明确目标

1．引导学生回忆“直角三角形锐角固定时，它的对边与斜边的比值、邻边与斜边的比值也是固定的．”

2．明确目标：这节课我们将研究直角三角形一锐角的对边、邻边与斜边的比值--正弦和余弦．

2．教学难点：用含有几个字母的符号组sinA、cosA表示正弦、余弦；正弦、余弦概念．

1．教学重点：使学生了解正弦、余弦概念．

(三)德育渗透点

渗透教学内容中普遍存在的运动变化、相互联系、相互转化等观点．

(二)能力训练点

逐步培养学生观察、比较、分析、概括的思维能力．

(一)知识教学点

使学生初步了解正弦、余弦概念；能够较正确地用sinA、cosA表示直角三角形中两边的比；熟记特殊角30°、45°、60°角的正、余弦值，并能根据这些值说出对应的锐角度数．

第十四章　 解直角三角形 　 一、锐角三角函数　　　　　　　　　 证明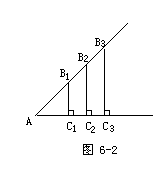：------------------ 结论：-------------------- 　 练习：---------------------

　正弦和余弦(二)

本节课内容较少，而且是为正、余弦概念打基础的，因此课后应要求学生预习正余弦概念．

(四)总结与扩展

1．引导学生作知识总结：本节课在复习勾股定理及含30°角直角三角形的性质基础上，通过动手实验、证明，我们发现，只要直角三角形的锐角固定，它的对边、邻边与斜边的比值也是固定的．

教师可适当补充：本节课经过同学们自己动手实验，大胆猜测和积极思考，我们发现了一个新的结论，相信大家的逻辑思维能力又有所提高，希望大家发扬这种创新精神，变被动学知识为主动发现问题，培养自己的创新意识．

2．扩展：当锐角为30°时，它的对边与斜边比值我们知道．今天我们又发现，锐角任意时，它的对边与斜边的比值也是固定的．如果知道这个比值，已知一边求其他未知边的问题就迎刃而解了．看来这个比值很重要，下节课我们就着重研究这个“比值”，有兴趣的同学可以提前预习一下．通过这种扩展，不仅对正、余弦概念有了初步印象，同时又激发了学生的兴趣．

(三)重点、难点的学习与目标完成过程

1．通过动手实验，学生会猜想到“无论直角三角形的锐角为何值，它的对边、邻边与斜边的比值总是固定不变的”．但是怎样证明这个命题呢？学生这时的思维很活跃．对于这个问题，部分学生可能能解决它．因此教师此时应让学生展开讨论，独立完成．

2．学生经过研究，也许能解决这个问题．若不能解决，教师可适当引导：

若一组直角三角形有一个锐角相等，可以把其

顶点A₁，A₂，A₃重合在一起，记作A，并使直角边AC₁，AC₂，AC₃……落在同一条直线上，则斜边AB₁，AB₂，AB₃……落在另一条直线上．这样同学们能解决这个问题吗？引导学生独立证明：易知，B₁C₁∥B₂C₂∥B₃C₃……，∴△AB₁C₁∽△AB₂C₂∽△AB₃C₃∽……，∴

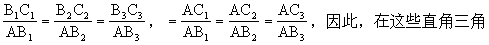
形中，∠A的对边、邻边与斜边的比值，是一个固定值．

通过引导，使学生自己独立掌握了重点，达到知识教学目标，同时培养学生能力，进行了德育渗透．

而前面导课中动手实验的设计，实际上为突破难点而设计．这一设计同时起到培养学生思维能力的作用．

练习题为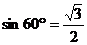作了孕伏同时使学生知道任意锐角的对边与斜边的比值都能求出来．