
6.已知有穷数列{an}(n=1,2,3,…,6)满足an∈{1,2,3,…,10},且当i≠j(i,j=1,2,3,…,6)时,ai≠aj.若a1>a2>a3,a4<a5<a6,则符合条件的数列{an}的个数是 ( )
A.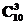
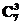 B.
B.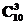
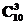 C.
C.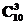
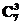 D.
D.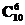
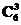
解析:先从10个数中任意选出3个,最大的数为a1,最小的为a3,另一数为a2,这样的选法有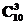 种;同理,从剩余的7个数中任选3个,有
种;同理,从剩余的7个数中任选3个,有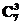 种选法,由分步计数原理知共有
种选法,由分步计数原理知共有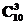
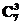 种选法.
种选法.
答案:A
5.(2009·全国卷Ⅱ)甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门不相同的选法共有 ( )
A.6种 B.12种 C.30种 D.36种
解析:从反面考虑: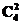 ·
·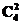 -
-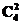 =6×6-6=30.
=6×6-6=30.
答案:C
4.某电视台连续播放6个广告,其中有3个不同的商业广告,2个不同的奥运宣传广告,1个公益广告.要求最后播放的不能是商业广告,且奥运宣传广告与公益广告不能连续播放,2个奥运宣传广告也不能连续播放,则不同的播放方法有________种.
解析:分三步:第一步,安排3个商业广告,有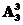 种不同的方法;第二步,从奥运宣传广告与公益广告中选择1个安排在最后一个播放,有
种不同的方法;第二步,从奥运宣传广告与公益广告中选择1个安排在最后一个播放,有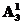 种不同的方法;第三步,把剩下的两个广告安排到3个商业广告分成的与第二步安排的广告不相邻的3个空位中,有
种不同的方法;第三步,把剩下的两个广告安排到3个商业广告分成的与第二步安排的广告不相邻的3个空位中,有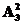 种不同方法,所以共有
种不同方法,所以共有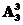
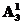
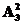 =108种方法.
=108种方法.
答案:108
|
题组二 |
组 合 问 题 |
3.从1,3,5,7中任取2个数字,从2,4,6,8中任取2个数字组成没有重复数字的四位数,其中能被5整除的四位数的个数有 ( )
A.120个 B.300个 C.240个 D.108个
解析:第一步:把5放到四位数的末位上;
第二步:从1,3,7中任取1个,有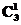 种方法;
种方法;
第三步:从2,4,6,8中任取2个数字,有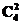 种方法;
种方法;
第四步:把选出的3个数字分别放在四位数的千位、百位与十位上,有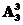 种方法.
种方法.
故共有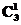
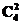
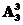 =108种方法.
=108种方法.
答案:D
2.(2010·桂林模拟)四张卡片上分别标有数字“2”“0”“0”“9”,其中“9”可当“6”用,则由这四张卡片可组成不同的四位数的个数为 ( )
A.6 B.12 C.18 D.24
解析:特殊元素优先处理,先在后三位中选两个位置填两个数字“0”,有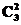 种填法,再决定用“9”还是“6”有两种可能,最后排另两个卡片有
种填法,再决定用“9”还是“6”有两种可能,最后排另两个卡片有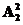 种排法,所以共可排成
种排法,所以共可排成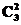 ·2·
·2·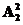 =12个四位数.
=12个四位数.
答案:B
1.将A、B、C、D、E排成一列,要求A、B、C在排列中顺序为“A、B、C”或“C、B、A”(可以不相邻),这样的排列数有多少种 ( )
A.12 B.20 C.40 D.60
解析:五个字母排成一列,①先从中选三个位置给A、B、C且A、B、C有两种排法,即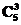 ×2,②然后让D、E排在剩余两个位置上,有
×2,②然后让D、E排在剩余两个位置上,有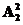 种排法;由分步乘法计数原理所求排列数为
种排法;由分步乘法计数原理所求排列数为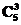 ×2×
×2×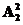 =40.
=40.
答案:C
24.选修4-5:不等式选讲
已知|x-4|+|3-x|<a
(1)若不等式的解集为空集,求a的范围
23. 选修4-4:几何证明选讲
在曲线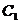 :
: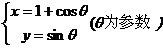 上求一点,使它到直线
上求一点,使它到直线
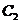 :
: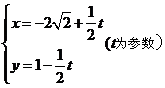 的距离最小,并求出该点坐标和最小距离。
的距离最小,并求出该点坐标和最小距离。
22.选修4-1:几何证明选讲
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,
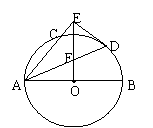 交AC的延长线于点E.OE交AD于点F.
交AC的延长线于点E.OE交AD于点F.
(1)求证:DE是⊙O的切线;
(2)若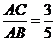 ,求
,求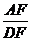 的值.
的值.
21.(本小题满分12分)
已知向量 ,
, ,
,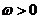 ,
,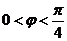 .函数
.函数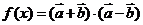 ,若
,若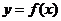 的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点
的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点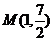 .
.
(Ⅰ)求函数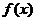 的表达式.
的表达式.
(Ⅱ)当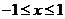 时,求函数
时,求函数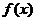 的单调区间.
的单调区间.
选考题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。本题满分10分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com