
2.求下列两条直线的夹角:
(1)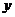 =3
=3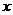 -1,
-1,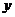 =-
=-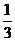
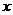 +4;
+4;
(2)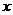 -
-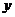 =5;
=5;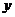 =4.
=4.
(3)5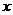 -3
-3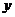 =9,6
=9,6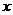 +10
+10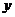 +7=0.
+7=0.
解:(1) 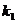 =3,
=3,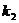 =-
=-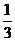 ,则 k1·
,则 k1·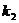 =-1,此时,两直线夹角为90°.
=-1,此时,两直线夹角为90°.
(tan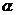 =
=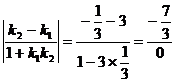 ,分母为0,正切值不存在).
,分母为0,正切值不存在).
(2) 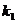 =1,
=1,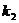 =0,tan
=0,tan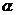 =
=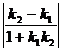 =1,∴
=1,∴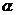 =45°,
=45°,
即两直线夹角为45°.
(3) 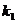 =
=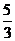 ,
,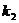 =-
=-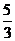 ,∴
,∴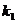 ·
·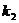 =-1,∴两直线夹角为90°
=-1,∴两直线夹角为90°
1.求下列直线 到
到 的角与
的角与 到
到 的角:
的角:
(1) :
: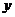 =
=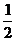
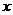 +2;
+2; :
: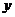 =3
=3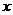 +7;
+7;
(2)  :
: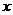 -
-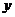 =5;
=5; :
: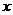 +2
+2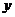 -3=0
-3=0
解:(1)∵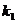 =
=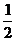 ,
,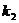 =3,∴设
=3,∴设 到
到 的角为
的角为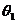 ,
,
则tan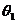 =
=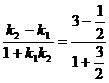 =1
=1 
∴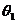 =45°即
=45°即 到
到 的角为45°.∴
的角为45°.∴ 到
到 的角为135°.
的角为135°.
(2)解:∵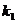 =1,
=1,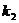 =-
=-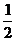

∴设 到
到 的角为
的角为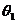 ,则
,则 到
到 的角为
的角为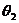 =π-
=π-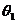
∴tan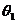 =
=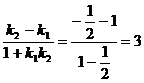 ,∴
,∴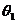 =π-arctan3.
=π-arctan3. 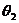 =arctan3
=arctan3
即 到
到 的角为π-arctan3,
的角为π-arctan3, 到
到 的角为arctan3
的角为arctan3 
例1 求直线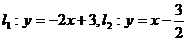 的夹角(用角度制表示)
的夹角(用角度制表示)
解:由两条直线的斜率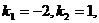 得
得
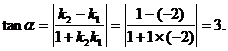
利用计算器计算或查表可得: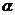 ≈71°34′
≈71°34′
说明:应用了两直线夹角公式,要求学生熟练掌握.
例2 等腰三角形一腰所在直线 的方程是
的方程是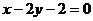 ,底边所在直线
,底边所在直线 的方程是
的方程是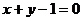 ,点(-2,0)在另一腰上,求这条腰所在直线
,点(-2,0)在另一腰上,求这条腰所在直线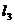 的方程.
的方程.
解:设 ,
, ,
,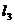 的斜率分别为
的斜率分别为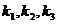 ,
,  到
到 的角是
的角是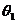 ,
,  到
到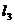 的角是
的角是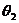 ,则
,则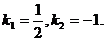
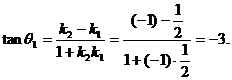
因为 ,
, ,
,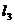 所围成的三角形是等腰三角形,所以
所围成的三角形是等腰三角形,所以
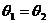 ,
, 即
即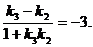
将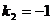 代入得
代入得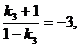 解得
解得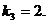
因为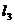 经过点(-2,0),斜率为2,写出其点斜式方程为
经过点(-2,0),斜率为2,写出其点斜式方程为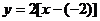 ,得:
,得: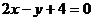 . 即直线
. 即直线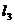 的方程
的方程
4.直线 ,
, 的夹角公式:
的夹角公式:
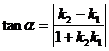

根据两直线的夹角定义可知,夹角在(0°,90°]范围内变化,所以夹角正切值大于或等于0.故可以由 到
到 的角取绝对值而得到
的角取绝对值而得到 与
与 的夹角公式.这一公式由夹角定义可得
的夹角公式.这一公式由夹角定义可得
3.直线 到
到 的角的公式:
的角的公式: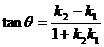 .
.
推导:设直线 到
到 的角
的角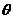 ,
,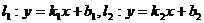 .
.
如果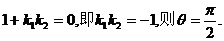
如果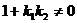 ,设
,设 ,
, 的倾斜角分别是
的倾斜角分别是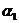 和
和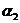 ,
,
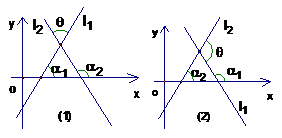 则
则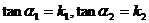 .
.
由图(1)和图(2)分别可知
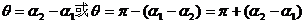
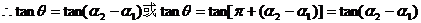
于是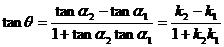

2.直线 到
到 的夹角定义:
的夹角定义:
如图, 到
到 的角是
的角是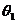 ,
,  到
到 的角是π-
的角是π-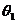 ,当
,当 与
与 相交但不垂直时,
相交但不垂直时, 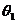 和π-
和π-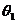 仅有一个角是锐角,我们把其中的锐角叫两条直线的夹角.
仅有一个角是锐角,我们把其中的锐角叫两条直线的夹角.
当直线 ⊥
⊥ 时,直线
时,直线 与
与 的夹角是
的夹角是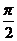 .
.
夹角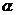 :0°<
:0°<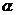 ≤90°.
≤90°.
说明: 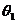 >0,
>0, 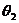 >0,且
>0,且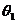 +
+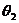 =π
=π
1.直线 到
到 的角的定义:
的角的定义:
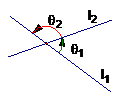 两条直线
两条直线 和
和 相交构成四个角,它们是两对对顶角,我们把直线
相交构成四个角,它们是两对对顶角,我们把直线 按逆时针方向旋转到与
按逆时针方向旋转到与 重合时所转的角,叫做
重合时所转的角,叫做 到
到 的角.
的角.
在图中,直线 到
到 的角是
的角是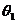 ,
,  到
到 的角是
的角是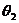 .
.
 到
到 的角
的角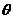 :0°<θ<180°.
:0°<θ<180°.
2.斜率存在时两直线的平行与垂直:
两条直线有斜率且不重合,如果它们平行,那么它们的斜率相等;反之,如果它们的斜率相等,则它们平行,即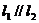
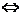
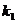 =
=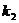 且
且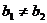
已知直线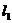 、
、 的方程为
的方程为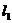 :
: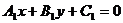 ,
,
 :
: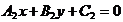
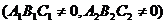
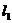 ∥
∥ 的充要条件是
的充要条件是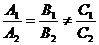

⑵两条直线垂直的情形:如果两条直线的斜率分别是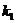 和
和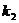 ,则这两条直线垂直的充要条件是
,则这两条直线垂直的充要条件是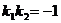 .
.
已知直线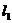 和
和 的一般式方程为
的一般式方程为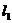 :
: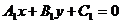 ,
,
 :
: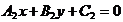 ,则
,则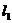
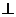

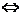
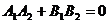

1.特殊情况下的两直线平行与垂直.
当两条直线中有一条直线没有斜率时:
(1)当另一条直线的斜率也不存在时,两直线的倾斜角都为90°,互相平行;
(2)当另一条直线的斜率为0时,一条直线的倾斜角为90°,另一条直线的倾斜角为0°,两直线互相垂直
34.读“二分二至时地球的位置”图,完成下列各题:(12分)
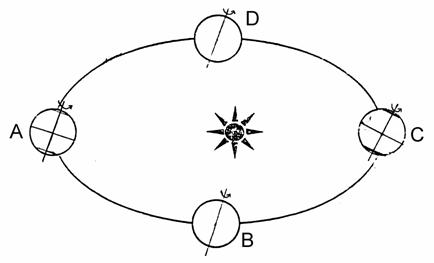
⑴在图中公转轨道上用箭头标出地球的公转方向。
⑵在地球位于A处时,北半球的节气是____________,太阳直射点所在的纬线是________
_________________________。
⑶当地球位于B处时,太阳直射在____________上,此时尉氏县的昼长为__________小时。
⑷在C处地球上画出晨昏线,并标出是晨线还是昏线;此时南半球进入_________(季节);北半球的昼夜长短状况___________________。
⑸当地球从C运动到D处时,上海的昼长_________(渐长或渐短),正午太阳高度________(变大或变小)。
选择题:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com