(四)总结与扩展

引导学生回忆前述例题，进行总结，以培养学生的概括能力．

1．弄清俯角、仰角、株距、坡度、坡角、水平距离、垂直距离、水位等概念的意义，明确各术语与示意图中的什么元素对应，只有明确这些概念，才能恰当地把实际问题转化为数学问题．

2．认真分析题意、画图并找出要求的直角三角形，或通过添加辅助线构造直角三角形来解决问题．

3．选择合适的边角关系式，使计算尽可能简单，且不易出错．

(三)重点、难点的学习与目标完成过程

1．坡度与坡角

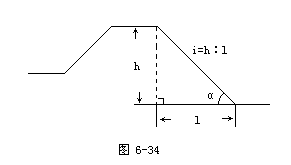
结合图6-34，教师讲述坡度概念，并板书：坡面的铅直高度h和水

平宽度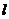的比叫做坡度(或叫做坡比)，一般用i表示。即i＝，

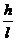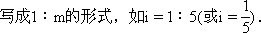
把坡面与水平面的夹角α叫做坡角．

引导学生结合图形思考，坡度i与坡角α之间具有什么关系？

　答：i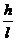＝＝tan

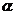
这一关系在实际问题中经常用到，教师不妨设置练习，加以巩固．

练习(1)一段坡面的坡角为60°，则坡度i=______；

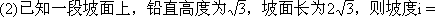
______，坡角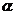______度．

为了加深对坡度与坡角的理解，培养学生空间想象力，教师还可以提问：

(1)坡面铅直高度一定，其坡角、坡度和坡面水平宽度有什么关系？举例说明．

(2)坡面水平宽度一定，铅直高度与坡度有何关系，举例说明．

答：(1)

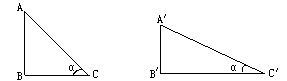
如图，铅直高度AB一定，水平宽度BC增加，α将变小，坡度减小，

因为 tan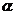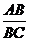＝，AB不变，tan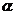随BC增大而减小

(2)

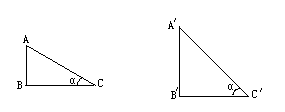
与(1)相反，水平宽度BC不变，α将随铅直高度增大而增大，tanα

　也随之增大，因为tan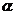=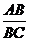不变时，tan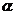随AB的增大而增大

2．讲授新课

引导学生分析例题，图中ABCD是梯形，若BE⊥AD，CF⊥AD，梯形就被分割成Rt△ABE，矩形BEFC和Rt△CFD，AD=AE+EF+FD，AE、DF可在△ABE和△CDF中通过坡度求出，EF=BC=6m，从而求出AD．

以上分析最好在学生充分思考后由学生完成，以培养学生逻辑思维能力及良好的学习习惯．

坡度问题计算过程很繁琐，因此教师一定要做好示范，并严格要求学生，选择最简练、准确的方法计算，以培养学生运算能力．

解：作BE⊥AD，CF⊥AD，在Rt△ABE和Rt△CDF中，

∴AE=3BE=3×23=69(m)．

FD=2.5CF=2.5×23=57.5(m)．

∴AD=AE+EF+FD=69+6+57.5=132.5(m)．

　因为斜坡AB的坡度i＝tan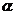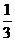＝≈0.3333，查表得

α≈18°26′

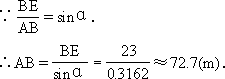
答：斜坡AB的坡角α约为18°26′，坝底宽AD为132.5米，斜坡AB的长约为72.7米．

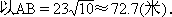
3．巩固练习

(1)教材P124. 2

由于坡度问题计算较为复杂，因此要求全体学生要熟练掌握，可能基础较好的学生会很快做完，教师可再给布置一题．

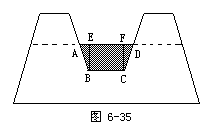
(2)利用土埂修筑一条渠道，在埂中间挖去深为0.6米的一块(图6-35阴影部分是挖去部分)，已知渠道内坡度为1∶1.5，渠道底面宽BC为0.5米，求：

①横断面(等腰梯形)ABCD的面积；

②修一条长为100米的渠道要挖去的土方数．

分析：1．引导学生将实际问题转化为数学问题．

2．要求S等腰梯形ABCD，首先要求出AD，如何利用条件求AD？

3．土方数=S·l

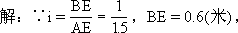
∴AE=1.5×0.6=0.9(米)．

∵等腰梯形ABCD，

∴FD=AE=0.9(米)．

∴AD=2×0.9+0.5=2.3(米)．

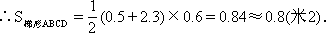
总土方数=截面积×渠长

=0.8×100=80(米3)．

答：横断面ABCD面积为0.8平方米，修一条长为100米的渠道要挖出的土方数为80立方米．

(二)整体感知

通过前面例题的教学，学生已基本了解解实际应用题的方法，会将实际问题抽象为几何问题加以解决．但此题中提到的坡度与坡角的概念对学生来说比较生疏，同时这两个概念在实际生产、生活中又有十分重要的应用，因此本节课关键是使学生理解坡度与坡角的意义．

(一)明确目标

1．讲评作业：将作业中学生普遍出现问题之处作一讲评．

2．创设情境，导入新课．

例　 同学们，如果你是修建三峡大坝的工程师，现在有这样一个问题请你解决：如图6-33

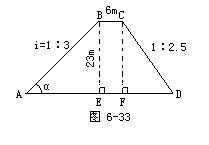
水库大坝的横断面是梯形，坝顶宽6m，坝高23m，斜坡AB的坡度i=1∶3，斜坡CD的坡度i=1∶2.5，求斜坡AB的坡面角α，坝底宽AD和斜坡AB的长(精确到0.1m)．

同学们因为你称他们为工程师而骄傲，满腔热情，但一见问题又手足失措，因为连题中的术语坡度、坡角等他们都不清楚．这时，教师应根据学生想学的心情，及时点拨．

3．疑点：对于坡度i表示成1∶m的形式学生易疏忽，教学中应着重强调，引起学生的重视．

2．难点：理解坡度的有关术语．

1．重点：解决有关坡度的实际问题．

(三)德育渗透点

培养学生用数学的意识，渗透理论联系实际的观点．

(二)能力训练点

逐步培养学生分析问题、解决问题的能力；渗透数形结合的数学思想和方法．

(一)知识教学点

巩固用三角函数有关知识解决问题，学会解决坡度问题．