20．(本小题满分12分)为防止某突发事件发生，有甲、乙、丙、丁四种相互独立的预防措施可供采用，单独采用甲、乙、丙、丁预防措施后此突发事件不发生的概率(记为P)和所需费用如下表：

预防方案可单独采用一种预防措施或联合采用几种预防措施．在总费用不超过120万元的前提下，请确定一个预防方案，使得此突发事件不发生的概率最大．

解：方案一：单独采用一种预防措施的费用均不超过120万元．由表可知，采用甲措施，可使此突发事件不发生的概率最大，其概率为0.9.

方案二：联合采用两种预防措施，费用不超过120万元．由表可知联合甲、丙两种预防措施可使此突发事件不发生的概率最大，其概率为1－(1－0.9)(1－0.7)＝0.97.

方案三：联合采用三种预防措施，费用不超过120万元，故只能联合乙、丙、丁三种预防措施，此时突发事件不发生的概率为

19．(本小题满分12分)甲、乙两人玩一种游戏，每次由甲、乙各出1到5根手指头，若和为偶数算甲赢，否则算乙赢．

(1)若以A表示和为6的事件，求P(A)．

(2)现连玩三次，若以B表示甲至少赢一次的事件，C表示乙至少赢两次的事件，试问B与C是否为互斥事件？为什么？

(3)这种游戏规则公平吗？试说明理由．

解：(1)基本事件空间与点集S＝{(x，y)|x∈N，y∈N,1≤x≤5,1≤y≤5}中的元素一一对应．

因为S中点的总数为5×5＝25(个)，所以基本事件总数为n＝25.

事件A包含的基本事件数共5个：

(1,5)、(2,4)、(3,3)、(4,2)、(5,1)，

所以P(A)＝＝.

(2)B与C不是互斥事件，因为事件B与C可以同时发生，如甲赢一次，乙赢两次的事件即符合．

(3)这种游戏规则不公平，由(1)知和为偶数的基本事件数为13个：

(1,1)、(1,3)、(1,5)、(2,2)、(2,4)、(3,1)、(3,3)、(3,5)、(4,2)、(4,4)、(5,1)、(5,3)、(5,5)

所以甲赢的概率为，乙赢的概率为.

所以这种游戏规则不公平．

18．(本小题满分12分)(2008·辽宁)某批发市场对某种商品的周销售量(单位：吨)进行统计，最近100周的统计结果如下表所示：

(1)根据上面统计结果，求周销售量分别为2吨，3吨和4吨的频率；

(2)若以上述频率作为概率，且各周的销售量相互独立，求：

(ⅰ)4周中该种商品至少有一周的销售量为4吨的概率；

(ⅱ)该种商品4周的销售量总和至少为15吨的概率．

解：(1)周销售量为2吨，3吨和4吨的频率分别为0.2,0.5和0.3.

(2)由题意知一周的销售量为2吨，3吨和4吨的概率分别为0.2,0.5和0.3，故所求的概率

(ⅰ)P₁＝1－0.7⁴＝0.7599.

(ⅱ)P₂＝C×0.5×0.3³+0.3⁴＝0.0621.

17．(本小题满分10分)甲、乙两人进行投篮训练，已知甲投球命中的概率是，乙投球命中的概率是.假设两人投球命中与否相互之间没有影响．

(1)如果两人各投球1次，求恰有1人投球命中的概率；

(2)如果两人各投球2次，求这4次投球中至少有1次命中的概率．

解：(1)记“甲投球1次命中”为事件A，“乙投球1次命中”为事件B.根据互斥事件的概率加法公式和相互独立事件的概率乘法公式，所求的概率是P(A·)+P(B·)＝P(A)·P()+P()·P(B)＝×(1－)+(1－)×＝.

(2)∵事件“两人各投球2次均不命中”的概率为＝×××＝，

∴两人各投球2次，这4次投球中至少有1次命中的概率为1－＝.

16．若在二项式(x+1)ⁿ(n>3且n∈N^*)的展开式中任取一项，该项的系数为奇数的概率是1，则在二项式(x+1)^n－1的展开式中任取一项，该项为奇数项的概率是p，为偶数项的概率是q，那么p－q＝________.

答案：

解析：由题意n为奇数，所以n－1为偶数，并且(x+1)^n－1的展开式有n项，其中奇数项比偶数项多一项，所以p＝＝，q＝＝.

所以p－q＝.

15．若随机从集合{2,2^2,2³，…，2¹⁰}中选出两个不同的元素a、b，则log_ab为整数的概率为________．

答案：

解析：a＝2时，有9个；

a＝2²时，b＝2⁴或2⁶或2⁸或2¹⁰，共4个；

a＝2³时，b＝2⁶或2⁹有2个；

a＝2⁴时，b＝2⁸有1个；

a＝2⁵时，b＝2¹⁰有1个；

使log_ab为整数的有17个，

∴概率为＝.

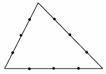
14．在三角形的每条边上各取三个分点(如右图)，以这9个分点为顶点可画出若干个三角形．若从中任意抽取一个三角形，则其三个顶点分别落在原三角形的三条不同边上的概率为________．(用数字作答)

答案：

解析：共作三角形数为C－3＝81，三顶点在三边上的三角形数为C×C×C＝27.

∴所求概率为＝.

13．若10把钥匙中只有2把能打开某锁，则从中任取2把能将该锁打开的概率为________．

答案：.

解析：所求概率为＝.

12．箱子里有5个黑球，4个白球，每次随机取出一个球，若取出黑球，则放回箱中，重新取球；若取出白球，则停止取球，那么在第4次取球之后停止的概率为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　 B．()³×

C.× 　　　　　　　　　　　　　　　　　　　　　　 D．C()³×

答案：B

解析：取出黑球的概率为，取出白球的概率为.

第4次取球之后停止说明前三次取出的都是黑球，第四次取出的是白球，故所求概率P＝()³×.

11．口袋里放有大小相等的两个红球和一个白球，有放回地每次摸取一个球，定义数列{a_n}：

a_n＝，如果S_n为数列{a_n}的前n项和，那么S₇＝3的概率为(　)

A．C()²·()⁵　 B．C()²·()⁵

C．C()²·()⁵　 D．C()²·()⁵

答案：B

解析：设在7次取球中，有x次拿了白球，则拿了(7－x)次红球，所以x×1+(7－x)×(－1)＝3.解得x＝5，所以求S₇＝3的概率就是求7次中取5次白球和2次红球的概率．每次取红球和白球的概率分别为、，

故其概率P＝C()²()⁵.