
3、三角形的外心:三角形三边垂直平分线的交点,即三角形外接圆的圆心。
2、三角形的外接圆:经过三角形三个顶点的圆。
1、不在同一条直线上的三个点确定一个圆。
3.(1)略 (2)4,(-2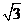 ,2)
,2)
知识点四、圆与三角形的关系
重点:掌握确定圆的条件、三角形的外心、内心
难点:确定圆的条件、三角形的外心、内心等知识熟练运用
2.BE的度数为80°,EF的度数为50°.
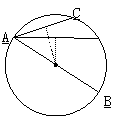
3.如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.
(1)求证:AB为⊙C直径.
(2)求⊙C的半径及圆心C的坐标.
 答案:1.(1)
AC、AD在AB的同旁,如右图所示:
答案:1.(1)
AC、AD在AB的同旁,如右图所示:
∵AB=16,AC=8,AD=8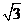 ,
,
∴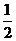 AC=
AC=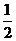 (
(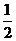 AB),∴∠CAB=6
AB),∴∠CAB=6 0°,
0°,
同理可得∠DAB=30°,
∴∠DAC=30°.
(2)AC、AD在AB的异旁,同理可得:∠DAC=60°+30°=90°.
2. 如图,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=50°,求弧BE的度数和弧EF的度数.
如图,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=50°,求弧BE的度数和弧EF的度数.
4、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角定理推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等。
圆周角定理推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径。
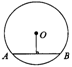 例1.如图,在半径为5cm的⊙O中,圆心O到弦AB的距离为3cm,则弦AB的长是( )
例1.如图,在半径为5cm的⊙O中,圆心O到弦AB的距离为3cm,则弦AB的长是( )
A.4cm B.6cm C.8cm D.10cm
解题思路:在一个圆中,若知圆的半径为R,弦长为a,圆心到此弦的距离为d,根据垂径定理,有R2=d2+(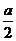 )2,所以三个量知道两个,就可求出第三个.答案C
)2,所以三个量知道两个,就可求出第三个.答案C
例2、如图,A、B、C、D是⊙O上的三点,∠BAC=30°,则∠BOC的大小是( )
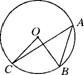 A、60° B、45°
C、30° D、15°
A、60° B、45°
C、30° D、15°
解题思路:运用圆周角与圆心角的关系定理,答案:A
例3、如图1和图2,MN是⊙O的直径,弦AB、CD相交于MN上的一点P,∠APM=∠CPM.
(1)由以上条件,你认为AB和CD大小关系是什么,请说明理由.
(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由.
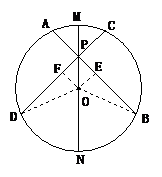
(1) (2)
解题思路:(1)要说明AB=CD,只要证明AB、CD所对的圆心角相等,只要说明它们的一半相等.
上述结论仍然成立,它的证明思路与上面的题目是一模一样的.
解:(1)AB=CD
理由:过O作OE、OF分别垂直于AB、CD,垂足分别为E、F
∵∠APM=∠CPM
∴∠1=∠2
OE=OF
连结OD、OB且OB=OD
∴Rt△OFD≌Rt△OEB
∴DF=BE
根据 垂径定理可得:AB=CD
垂径定理可得:AB=CD
(2)作OE⊥ AB,OF⊥CD,垂足为E、F
AB,OF⊥CD,垂足为E、F
∵∠APM=∠CPN且OP=OP,∠PEO=∠PFO=90°
∴Rt△OPE≌Rt△OPF
∴OE=OF
连接OA、OB、OC、OD
易证Rt△OBE≌Rt△ODF,Rt△OAE≌Rt△OCF
∴∠1+∠2=∠3+∠4
∴AB=CD
例4.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?
 解题思路:BD=CD,因为AB=AC,所以这个△ABC是等腰,要证明D是BC的中点,只要连结AD证明AD是高或是∠BAC的平分线即可.
解题思路:BD=CD,因为AB=AC,所以这个△ABC是等腰,要证明D是BC的中点,只要连结AD证明AD是高或是∠BAC的平分线即可.
解:BD=CD
理由是:如图24-30,连接AD
∵AB是⊙O的直径
∴∠ADB=90°即AD⊥BC
又∵AC=AB
∴BD=CD
练习
1: AB是⊙O的直径,AC、AD是⊙O的两弦,已知AB=16,AC=8,AD=8,求∠DAC的度数.
3、圆具有旋转对称性,特别的圆是中心对称图形,对称中心是圆心。
圆心角定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
2、垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦对的弧。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com