
1、B
6、已知锌板的极限波长λO=372nm,氢原子的基态能量为-13.6eV,若氢原子的核外电子从量子数n=2跃迁到n=1时所发出的光子照射到该锌板上,此时能否产生光电效应?若能,光电子的最大初动能是多少电子伏?(真空中光速c=3×108m/s,普朗克常量h=6.63×10-34J·s,电子电荷量e=1.6×10-19C)
课堂练习答案:
5、太阳光垂直射到地面上时,1m2地面接受的太阳光的功率为1.4kW,其中可见光部分约占45%。
⑴假如认为可见光的波长约为0.55μm,日地间距离R=1.5×1011m,普朗克恒量h=6.6×10-34J·s,估算太阳每秒辐射出的可见光光子为多少。
⑵若已知地球的半径r=6.4×106m,估算地球接受的太阳光的总功率。
4、神光“II”装置是我国规模最大、国际上为数不多的高功率固体激光系统,利用它可获得能量为2400J、波长λ为0.35μm的紫外激光。已知普朗克恒星h=6.63×10-34J·s,则该紫外激光所含光子数为多少个。(取两位有效数字)
3、下列说法正确的是:
A、光波是一种概率波 B、光波是一种电磁波
C、单色光从密介质进入光疏介质时,光子的能量改变
D、单色光从光密介质进入光疏介质时,光的波长不变
2、a、b是两束相互平行的单色可见光,当它们从空气射入水中时各自发生如图所示的折射现象,已知折射角r1>r2,由此可以判定( )
①a光光子能量小;②在水中b光波长长一些;③让它们在同一双缝上发生干涉,所得相邻两条干涉条纹间距△xa>△xb;④a、b从水中射入空气时,则a光的临界角小一些。
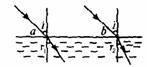 A、只有①② B、只有①③
A、只有①② B、只有①③
C、只有②④ D、只有②③
1、先后用两种不同的单色光,在相同的条件下用同一双缝干涉装置做实验,在屏幕上相邻的两条亮纹间距不同,其中间距较大的那种单色光比另一种单色光①在真空中的波长较短 ②在玻璃中传播速度较大 ③在玻璃中传播时,玻璃的折射率较大 ④其光子的能量较小 以上说法正确的是( )
A、①③ B、②④ C、①④ D、②③
[例1]在双缝干涉实验中,以白光为光源,在屏幕上观察到了彩色干涉条纹,若在双缝中的一缝前放一红色滤光片(只能透过红光),另一缝前放一绿色滤光片(只能透过绿光),这时( )
A、只有红色和绿色的双缝干涉条纹,其他颜色的双缝干涉条纹消失
B、红色和绿色的双缝干涉条纹消失,其他颜色的双缝干涉条纹依然存在
C、任何颜色的双缝干涉条纹都不存在,但屏上仍有光亮
D、屏上无任何光亮
[解析]在双缝干涉实验的装置中,缝的宽度跟光的波长相差不多,在双缝分别放上红色和绿色滤光片之后,由于红光和绿光的频率不相等,在光屏上不可再出现干涉条纹了,但由于满足产生明显衍射现象的条件,所以在屏上将同时出现红光和绿光的衍射条纹,故正确的选项为C。
[例2]某金属在一束黄光照射下,恰好能有电子逸出(即用频率小于这种黄光的光线照射就不可能有电子逸出),在下述情况下,逸出电子的多少和电子的最大初动能会发生什么变化?
⑴增大光强而不改变光的频率;
⑵用一束强度更大的红光代替黄光;
⑶用强度相同的紫光代替黄光。
[解析]“正好有电子逸出”,说明此种黄光的频率恰为该种金属的极限频率。
⑴增大光强而不改变光的频率,意味着单位时间内入射光子数增多而每个光子能量不变,根据爱因斯坦光电效应方程,逸出的光电子最大初动能不变,但光电子数目增大。
⑵用一束强度更大的红光代替黄光,红光光子的频率小于该金属的极限频率,所以无光电子逸出。
⑶用强度相同的紫光代替黄光,因为一个紫光光子的能量大于一个黄光光子的能量,而强度相同,因而单位时间内射向金属的紫光光子数将比原来少,因此,逸出的电子数将减少,但据爱因斯坦光电效应方程,光电子的最大初动能将增大。
[例3]把一个凸透镜的弯曲表面压在另一个玻璃平面上,让光从上方射入(图甲),这时可以看到亮暗相间的同心圆(图乙),这个现象是牛顿首先发现的,这些同心圆叫做牛顿环,解释为什么会出现牛顿环。
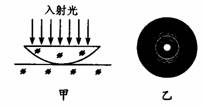
[解析]凸透镜的弯曲上表面反射的光和下面的玻璃平面向上反射的光相互叠加,由于来自这两个面的反射的光的路程差不同,在有些位置相互加强,在有些位置相互削弱,因此出现了同心圆状的明暗相间的条纹。
[例4]把一个平行玻璃板压在另一个平行玻璃板上,一端用薄片垫起,构成空气劈尖,让单色光从上方射入(如图),这时可以看到亮暗相间的条纹,下面关于条纹的说法中正确的是( )
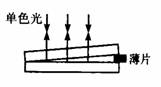 A、将薄片向着劈尖移动使劈角变大时,条纹变疏
A、将薄片向着劈尖移动使劈角变大时,条纹变疏
B、将薄片远离劈尖移动使劈角变小时,条纹变疏
C、将上玻璃板平行上移,条纹向着劈尖移动
D、将上玻璃板平行上移,条纹远离劈尖移动
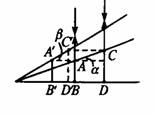 [解析]楔形空气层的上下两个表面反射的两列光波发生干涉,空气层厚度相同的地方,两列波的路程差相同,故如果被测表面是平的,干涉条纹就是一组平行的直线,如上图,当劈角为α时,相邻两条纹间等于
[解析]楔形空气层的上下两个表面反射的两列光波发生干涉,空气层厚度相同的地方,两列波的路程差相同,故如果被测表面是平的,干涉条纹就是一组平行的直线,如上图,当劈角为α时,相邻两条纹间等于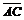 ,当劈角增大为β时,相邻的条纹左移至A’、C’处,条纹间距变为
,当劈角增大为β时,相邻的条纹左移至A’、C’处,条纹间距变为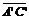 。设
。设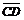 -
-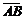 =△s,则
=△s,则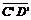 -
-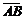 =△s,故
=△s,故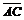 =
=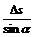 ,
,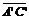 =
=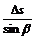 。
。
因为β>α,所以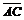 >
>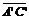 ,故劈角增大时,条纹变密。
,故劈角增大时,条纹变密。
同理,当上玻璃板平行上移时,易得A’C’CA为平行四边形,所以条纹向壁尖移动,且间距不变,本题选B、C。
2、 如图示:光从A点射入圆形玻璃,并从B点射出,若射出玻璃与射入玻璃的光线夹角为30°,AB弧所对的圆心角为120°,下列说法正确的是:( C )
A. 在A点的入射角为30°
B. 在B点的入射角为45°
C. 玻璃的折射率为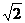
D. 玻璃的折射率为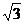
解:光路图作,由于对称性,∠1=60 ° ∠2=15 ° ∠i =45
|
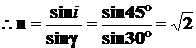 ∠4=∠r =∠3= 1/2 ∠1=30°
∠4=∠r =∠3= 1/2 ∠1=30°
3:如图,a和b 都是厚度均匀的平玻璃板,它们之间的夹角为φ,一细光束以入射角θ从P点射入,θ > φ,已知此光束由红光和蓝光组成,则当光束透过b板后, ( D )
A.传播方向相对于入射光方向向左偏转φ角
B.传播方向相对于入射光方向向右偏转φ角
 C.红光在蓝光的左边
C.红光在蓝光的左边
D.红光在蓝光的右边
二计算题
4: 光屏MN 和遮光板PQ彼此平行地竖直放置,它们相距10cm,遮光板PQ上有一直径为1cm 的圆形透光孔ab,位于遮光板左侧20cm 处有一点光源S,如图示,在点光源S下方水平放置一块平面镜使点光源发出的光通过圆孔ab后在光屏MN上形成两个光斑,两个光斑外边缘上下距离为5.5cm,作图计算平面镜距点光源的竖直距离。
解:作光路图,由相似关系AB=A1B1=1.5cm A1B=5.5cm ∴ BB1 =4cm ΔBB1b ∽ ΔSS1b SS1 / BB1 = SS 1/Aa=2
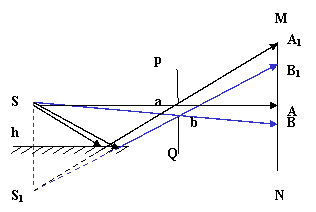 ∴ SS1 =8cm h=1/2×SS1 =4cm
∴ SS1 =8cm h=1/2×SS1 =4cm
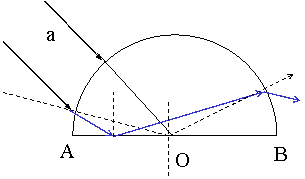
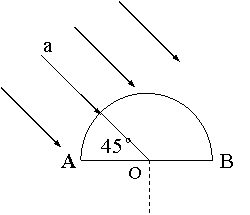 5: 如图示,一束平行光照射在半径为R的半圆柱形玻璃砖的圆柱面上,光线a是与一条半径重合的光线,该光线照射到圆心O点与直径AB夹角为45°,且刚好发生全反射.请作图并确定出光线能从AB面射出的范围.
5: 如图示,一束平行光照射在半径为R的半圆柱形玻璃砖的圆柱面上,光线a是与一条半径重合的光线,该光线照射到圆心O点与直径AB夹角为45°,且刚好发生全反射.请作图并确定出光线能从AB面射出的范围.
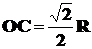 答案;
答案;
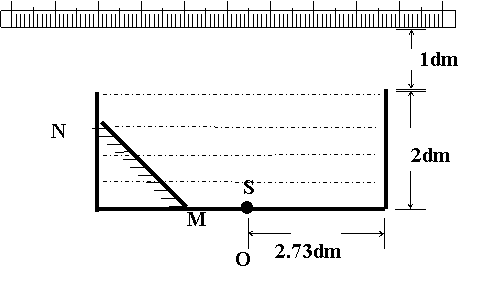
6:如图示,一不透明的圆柱形容器内装满折射率n =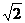 的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底面半径为(1+
的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底面半径为(1+ 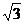 )dm,OM=1dm,在容器中央正上方1dm 处水平水平放置一足够长的刻度尺,求光源S 发出的光经平面镜反射后,照射到刻度尺上的长度。(不考虑容器侧壁和液面的反射)
)dm,OM=1dm,在容器中央正上方1dm 处水平水平放置一足够长的刻度尺,求光源S 发出的光经平面镜反射后,照射到刻度尺上的长度。(不考虑容器侧壁和液面的反射)
解:作出光路图如图示:由几何关系得:M S' = M S =1dm
S'P=3dm PQ= 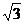 dm
dm
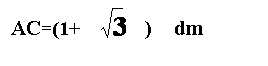 答案
答案
1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com