
2.表(侧)面积与体积公式:
⑴柱体:①表面积:S=S侧+2S底;②侧面积:S侧=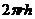 ;③体积:V=S底h
;③体积:V=S底h
 ⑵锥体:①表面积:S=S侧+S底;②侧面积:S侧=
⑵锥体:①表面积:S=S侧+S底;②侧面积:S侧=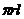 ;③体积:V=
;③体积:V=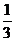 S底h:
S底h:
⑶台体①表面积:S=S侧+S上底S下底②侧面积:S侧=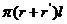 ③体积:V=
③体积:V=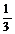 (S+
(S+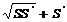 )h;
)h;
⑷球体:①表面积:S=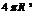 ;②体积:V=
;②体积:V=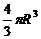
1.(1)三视图包括:正视图:物体 方向投影所得到投影图;它能反映物体高度和长度;左视图:物体 方向投影所得到投影图;它能反映物体高度和宽度;俯视图:物体 方向投影所得到投影图;它能反映物体的长度和宽度;
 (2)三视图画法规则:高平齐: 图与 图高要保持平齐;长对正: 图与 图长应对正; 宽相等: 图与 图宽度应相等;先画主视图,其次画俯视图,最后画左视图。画的时候把轮廓线要画出来,被遮住的轮廓线要画成 。
(2)三视图画法规则:高平齐: 图与 图高要保持平齐;长对正: 图与 图长应对正; 宽相等: 图与 图宽度应相等;先画主视图,其次画俯视图,最后画左视图。画的时候把轮廓线要画出来,被遮住的轮廓线要画成 。
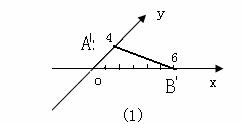
(3)斜二测画法应注意的地方:
(1)在已知图形中取互相垂直的轴Ox、Oy。画直观图时,
把它画成对应轴 o'x'、o'y'、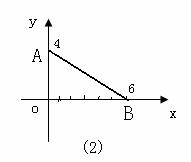 使∠x'o'y'=45°(或135° );
使∠x'o'y'=45°(或135° );
(2)平行于x轴的线段长不变,平行于y轴的线段长减半.
(3)直观图中的45度原图中就是90度,直观图中的90度原图一定不是90度.
如图(1),三角形ABO的面积是6;
7.解析几何与向量综合的有关结论:
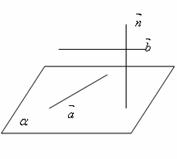
⑴给出直线的方向向量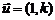 或
或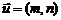 .等于已知直线的斜率
.等于已知直线的斜率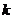 或
或 ;
;
⑵给出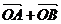 与
与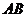 相交,等于已知
相交,等于已知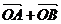 过
过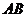 的中点;
的中点;
⑶给出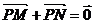 ,等于已知
,等于已知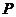 是
是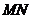 的中点;
的中点;
⑷给出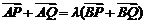 ,等于已知
,等于已知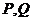 与
与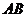 的中点三点共线;
的中点三点共线;
⑸给出以下情形之一: ①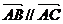 ; ②存在实数
; ②存在实数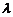 ,使
,使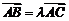 ; ③若存在实数
; ③若存在实数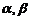 ,
,
且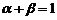 ;使
;使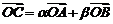 ,等于已知
,等于已知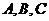 三点共线.
三点共线.
⑹在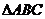 中,给出
中,给出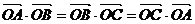 ,等于已知
,等于已知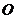 是
是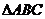 的垂心(三角形的垂心是三角形三条高的交点).
的垂心(三角形的垂心是三角形三条高的交点).
⑺给出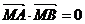 ,等于已知
,等于已知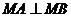 ,即
,即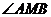 是直角,给出
是直角,给出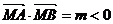 ,等于已
,等于已
知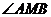 是钝角或反向共线,给出
是钝角或反向共线,给出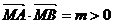 ,等于已知
,等于已知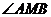 是锐角或同向共线.
是锐角或同向共线.
⑻在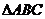 中,给出
中,给出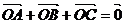 ,等于已知
,等于已知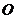 是
是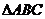 的重心(三角形的重心是三角形三条中线的交点).
的重心(三角形的重心是三角形三条中线的交点).
⑼在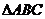 中,给出
中,给出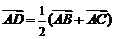 ,等于已知
,等于已知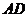 是
是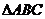 中
中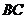 边的中线..
边的中线..
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
6. 若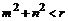 ,则点
,则点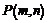 在圆
在圆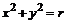 的内部;
的内部;
椭圆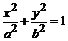 ,内部任意一点
,内部任意一点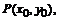 必将对应椭圆上一个点
必将对应椭圆上一个点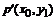 ,其中
,其中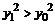 。因此,
。因此,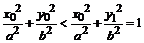 。
。
抛物线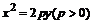 内部一点
内部一点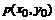 ,在抛物线上对应一点
,在抛物线上对应一点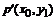 ,其中
,其中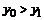 ,
,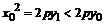 ,即
,即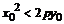 。其它情况得到同样结论。
。其它情况得到同样结论。
双曲线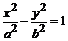 ,内部任意一点
,内部任意一点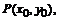 必将对应双曲线上一个点
必将对应双曲线上一个点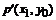 ,其中
,其中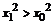 。因此,
。因此,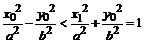 。可见双曲线的内部应该是双曲线的两支之间的部分。
。可见双曲线的内部应该是双曲线的两支之间的部分。
5.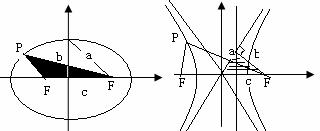 圆锥曲线中点弦问题:遇到中点弦问题常用“韦达定理”或“点差法”求解.在椭圆
圆锥曲线中点弦问题:遇到中点弦问题常用“韦达定理”或“点差法”求解.在椭圆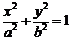 中,以
中,以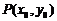 为中点的弦所在直线斜率
为中点的弦所在直线斜率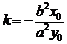 ;在双曲线
;在双曲线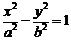 中,以
中,以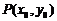 为中点的弦所在直线斜率
为中点的弦所在直线斜率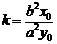 ;在抛物线
;在抛物线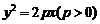 中,以
中,以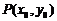 为中点的弦所在直线的斜率
为中点的弦所在直线的斜率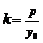 .
.
4.结论 ⑴焦半径:①椭圆: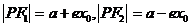 (e为离心率); (左“+”右“-”);②抛物线:
(e为离心率); (左“+”右“-”);②抛物线: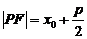 ⑵弦长公式:
⑵弦长公式: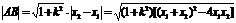
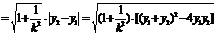 ;
;
⑶过两点椭圆、双曲线标准方程可设为: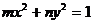 (
(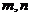 同时大于0时表示椭圆,
同时大于0时表示椭圆,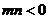 时表示双曲线);
时表示双曲线);
⑷椭圆中的结论:①内接矩形最大面积 :2ab; ②P,Q为椭圆上任意两点,且OP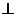 0Q,则
0Q,则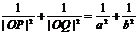 ;
;
③椭圆焦点三角形:<Ⅰ>.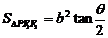 ,(
,(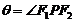 );<Ⅱ>.点
);<Ⅱ>.点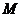 是
是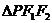 内心,
内心,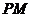 交
交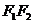 于点
于点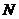 ,则
,则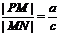 ; ④当点
; ④当点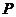 与椭圆短轴顶点重合时
与椭圆短轴顶点重合时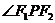 最大;
最大;
⑸双曲线中的结论:①双曲线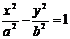 (a>0,b>0)的渐近线:
(a>0,b>0)的渐近线: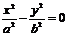 ; ②共渐进线
; ②共渐进线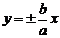 的双曲线标准方程为
的双曲线标准方程为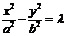 ;④双曲线为等轴双曲线
;④双曲线为等轴双曲线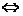
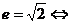 渐近线为
渐近线为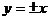
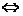 渐近线互相垂直;
渐近线互相垂直;
③双曲线焦点三角形:<Ⅰ>.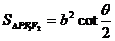 ,(
,(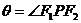 );<Ⅱ>.P是双曲线
);<Ⅱ>.P是双曲线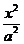 -
-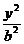 =1(a>0,b>0)的左(右)支上一点,F1、F2分别为左、右焦点,则△PF1F2的内切圆的圆心横坐标为
=1(a>0,b>0)的左(右)支上一点,F1、F2分别为左、右焦点,则△PF1F2的内切圆的圆心横坐标为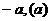 ;
;
(6)抛物线中的结论:
①抛物线y2=2px(p>0)的焦点弦AB性质:<Ⅰ>. x1x2=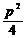 ;y1y2=-p2;<Ⅱ>.
;y1y2=-p2;<Ⅱ>.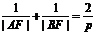 ;<Ⅲ>.以AB为直径的圆与准线相切;<Ⅳ>.以AF(或BF)为直径的圆与
;<Ⅲ>.以AB为直径的圆与准线相切;<Ⅳ>.以AF(或BF)为直径的圆与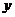 轴相切;<Ⅴ>.
轴相切;<Ⅴ>.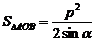 。
。
②抛物线y2=2px(p>0)内结直角三角形OAB的性质:<Ⅰ>.
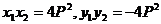 ;
;
<Ⅱ>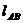 恒过定点
恒过定点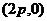 ;<Ⅲ>
;<Ⅲ>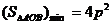
<Ⅴ>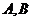 中点轨迹方程:
中点轨迹方程: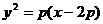 ;<Ⅳ>.
;<Ⅳ>.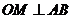 ,则
,则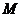 轨迹方程为:
轨迹方程为: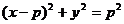 ;
;
③抛物线y2=2px(p>0),对称轴上一定点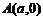 ,则:<Ⅰ>.当
,则:<Ⅰ>.当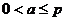 时,顶点到点A距离最小,最小值为
时,顶点到点A距离最小,最小值为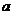 ;<Ⅱ>.当
;<Ⅱ>.当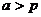 时,抛物线上有关于
时,抛物线上有关于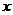 轴对称的两点到点A距离最小,最小值为
轴对称的两点到点A距离最小,最小值为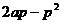 。
。
3.抛物线 ①方程y2=2px ; ②定义:|PF|=d准;③顶点为焦点到准线垂线段中点;x,y范围?轴?焦点F(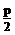 ,0),准线x=-
,0),准线x=-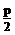 ,
,
④焦半径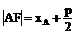 ; 焦点弦
; 焦点弦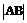 =x1+x2+p; y1y2=-p2, x1x2=
=x1+x2+p; y1y2=-p2, x1x2=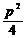 其中A(x1,y1)、B(x2,y2)
⑤通径2p,焦准距p;
其中A(x1,y1)、B(x2,y2)
⑤通径2p,焦准距p;
2.双曲线 :①方程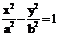 (a,b>0);②定义: ||PF1|-|PF2||=2a<2c; ③e=
(a,b>0);②定义: ||PF1|-|PF2||=2a<2c; ③e=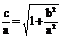 ,c2=a2+b2; ④四点坐标?x,y范围?实虚轴、渐进线交点为中心; ⑤到焦点距离常化为到准线距离; ⑥准线x=
,c2=a2+b2; ④四点坐标?x,y范围?实虚轴、渐进线交点为中心; ⑤到焦点距离常化为到准线距离; ⑥准线x=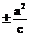 、通径(最短焦点弦)
、通径(最短焦点弦)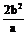 ,
,
焦准距p=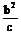 ⑦
⑦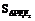 =
=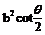 ⑧渐进线
⑧渐进线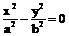 或
或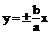 ; 焦点到渐近线距离为b;
; 焦点到渐近线距离为b;
1.
椭圆: ①方程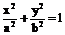 (a>b>0);参数方程
(a>b>0);参数方程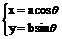 ; ②定义: |PF1|+|PF2|=2a>2c; ③ e=
; ②定义: |PF1|+|PF2|=2a>2c; ③ e=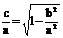 ④长轴长为2a,短轴长为2b; ⑤准线x=
④长轴长为2a,短轴长为2b; ⑤准线x=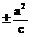 、通径(最短焦点弦)
、通径(最短焦点弦)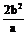 ,焦准距p=
,焦准距p=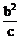 ,a2=b2+c2 ;
,a2=b2+c2 ;
⑥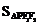 =
=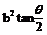 ,当P为短轴端点时∠PF1F2最大; 近地a-c ,远地a+c;
,当P为短轴端点时∠PF1F2最大; 近地a-c ,远地a+c;
17. 若直线mx+y+2=0与线段AB有交点,其中A(-2, 3),B(3,2),求实数m的取值范围。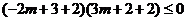 ,解得
,解得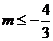 或m≥
或m≥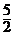 。
。
已知圆C的方程为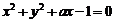 ,若
,若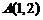 ,
,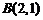 两点一个在圆C的内部,一个在圆C的外部,则实数a的取值范围是
.
两点一个在圆C的内部,一个在圆C的外部,则实数a的取值范围是
.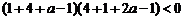 ,解得
,解得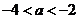 。
。
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com