
6、多项式函数的单调性:
(1)多项式函数的导数与函数的单调性:
①若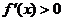 ,则
,则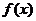 为增函数;若
为增函数;若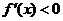 ,则
,则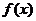 为减函数;若
为减函数;若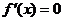 恒成立,则
恒成立,则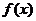 为常数函数;若
为常数函数;若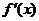 的符号不确定,则
的符号不确定,则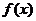 不是单调函数。
不是单调函数。
②若函数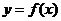 在区间(
在区间(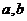 )上单调递增,则
)上单调递增,则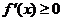 ,反之等号不成立;若函数
,反之等号不成立;若函数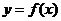 在区间(
在区间(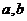 )上单调递减,则
)上单调递减,则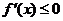 ,反之等号不成立。如(1)函数
,反之等号不成立。如(1)函数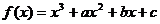 ,其中
,其中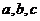 为实数,当
为实数,当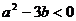 时,
时,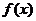 的单调性是______(答:增函数);(2)设
的单调性是______(答:增函数);(2)设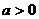 函数
函数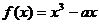 在
在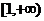 上单调函数,则实数
上单调函数,则实数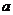 的取值范围______(答:
的取值范围______(答: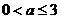 );(3)已知函数
);(3)已知函数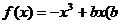 为常数)在区间
为常数)在区间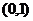 上单调递增,且方程
上单调递增,且方程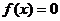 的根都在区间
的根都在区间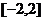 内,则
内,则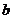 的取值范围是____________(答:
的取值范围是____________(答: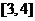 );(4)已知
);(4)已知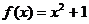 ,
,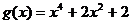 ,设
,设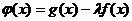 ,试问是否存在实数
,试问是否存在实数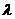 ,使
,使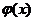 在
在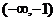 上是减函数,并且在
上是减函数,并且在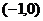 上是增函数?(答:
上是增函数?(答: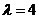 )
)
(2)利用导数求函数单调区间的步骤:(1)求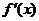 ;(2)求方程
;(2)求方程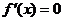 的根,设根为
的根,设根为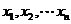 ;(3)
;(3)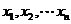 将给定区间分成n+1个子区间,再在每一个子区间内判断
将给定区间分成n+1个子区间,再在每一个子区间内判断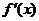 的符号,由此确定每一子区间的单调性。如设函数
的符号,由此确定每一子区间的单调性。如设函数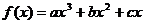 在
在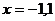 处有极值,且
处有极值,且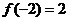 ,求
,求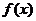 的单调区间。(答:递增区间(-1,1),递减区间
的单调区间。(答:递增区间(-1,1),递减区间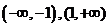 )
)
5、导数的运算法则:(1)常数函数的导数为0,即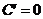 (C为常数); (2)
(C为常数); (2)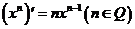 ,与此有关的如下:
,与此有关的如下: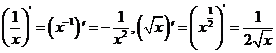 ;(3)若
;(3)若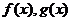 有导数,则①
有导数,则①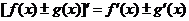 ;②
;②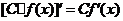 。如(1)已知函数
。如(1)已知函数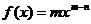 的导数为
的导数为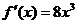 ,则
,则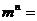 _____(答:
_____(答: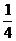 );(2)函数
);(2)函数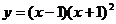 的导数为__________(答:
的导数为__________(答: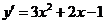 );(3)若对任意
);(3)若对任意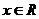 ,
,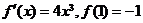 ,则
,则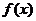 是______(答:
是______(答: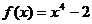 )
)
4、导数的几何意义:函数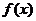 在点
在点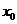 处的导数的几何意义,就是曲线
处的导数的几何意义,就是曲线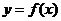 在点
在点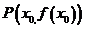 处的切线的斜率,即曲线
处的切线的斜率,即曲线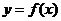 在点
在点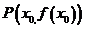 处的切线的斜率是
处的切线的斜率是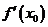 ,相应地切线的方程是
,相应地切线的方程是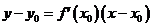 。特别提醒:(1)在求曲线的切线方程时,要注意区分所求切线是曲线上某点处的切线,还是过某点的切线:曲线上某点处的切线只有一条,而过某点的切线不一定只有一条,即使此点在曲线上也不一定只有一条;(2)在求过某一点的切线方程时,要首先判断此点是在曲线上,还是不在曲线上,只有当此点在曲线上时,此点处的切线的斜率才是
。特别提醒:(1)在求曲线的切线方程时,要注意区分所求切线是曲线上某点处的切线,还是过某点的切线:曲线上某点处的切线只有一条,而过某点的切线不一定只有一条,即使此点在曲线上也不一定只有一条;(2)在求过某一点的切线方程时,要首先判断此点是在曲线上,还是不在曲线上,只有当此点在曲线上时,此点处的切线的斜率才是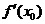 。如(1)P在曲线
。如(1)P在曲线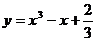 上移动,在点P处的切线的倾斜角为α,则α的取值范围是______(答:
上移动,在点P处的切线的倾斜角为α,则α的取值范围是______(答: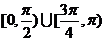 );(2)直线
);(2)直线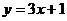 是曲线
是曲线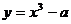 的一条切线,则实数
的一条切线,则实数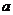 的值为_______(答:-3或1);(3)已知函数
的值为_______(答:-3或1);(3)已知函数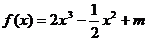 (
(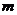 为常数)图象上
为常数)图象上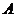 处的切线与
处的切线与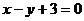 的夹角为
的夹角为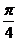 ,则
,则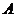 点的横坐标为_____(答:0或
点的横坐标为_____(答:0或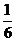 );(4)曲线
);(4)曲线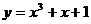 在点
在点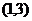 处的切线方程是______________(答:
处的切线方程是______________(答: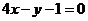 );(5)已知函数
);(5)已知函数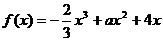 ,又导函数
,又导函数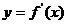 的图象与
的图象与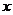 轴交于
轴交于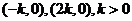 。①求
。①求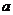 的值;②求过点
的值;②求过点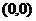 的曲线
的曲线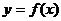 的切线方程(答:①1;②
的切线方程(答:①1;②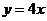 或
或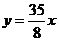 )。
)。
3、求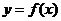 在
在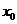 处的导数的步骤:(1)求函数的改变量
处的导数的步骤:(1)求函数的改变量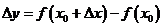 ;(2)求平均变化率
;(2)求平均变化率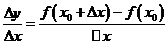 ;(3)取极限,得导数
;(3)取极限,得导数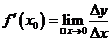 。
。
2、导函数的概念:如果函数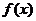 在开区间(a,b)内可导,对于开区间(a,b)内的每一个
在开区间(a,b)内可导,对于开区间(a,b)内的每一个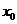 ,都对应着一个导数
,都对应着一个导数 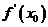 ,这样
,这样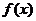 在开区间(a,b)内构成一个新的函数,这一新的函数叫做
在开区间(a,b)内构成一个新的函数,这一新的函数叫做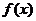 在开区间(a,b)内的导函数, 记作
在开区间(a,b)内的导函数, 记作 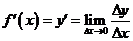
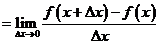 ,导函数也简称为导数。
,导函数也简称为导数。
1、导数的背景:(1)切线的斜率;(2)瞬时速度;(3)边际成本。 如一物体的运动方程是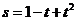 ,其中
,其中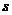 的单位是米,
的单位是米,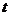 的单位是秒,那么物体在
的单位是秒,那么物体在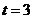 时的瞬时速度为_____(答:5米/秒)
时的瞬时速度为_____(答:5米/秒)
(二)减少填空题失分的检验方法
1、回顾检验
例18、满足条件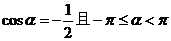 的角
的角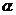 的集合为 。
的集合为 。
错解: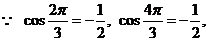
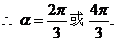
检验:根据题意,答案中的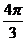 不满足条件
不满足条件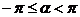 ,应改为
,应改为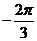 ;其次,角
;其次,角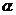 的取值要用集合表示。故正确答案为
的取值要用集合表示。故正确答案为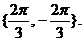
2、赋值检验。若答案是无限的、一般性结论时,可赋予一个或几个特殊值进行检验,以避免知识性错误。
例19、已知数列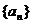 的前n项和为
的前n项和为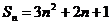 ,则通项公式
,则通项公式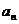 = 。
= 。
错解: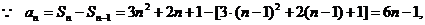
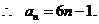
检验:取n=1时,由条件得 ,但由结论得a1=5。
,但由结论得a1=5。
故正确答案为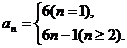
3、逆代检验。若答案是有限的、具体的数据时,可逐一代入进行检验,以避免因扩大自变量的允许值范围而产生增解致错。
例20、方程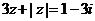 的解是 。
的解是 。
错解:设 ,则
,则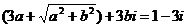 ,根据复数相等的定义得
,根据复数相等的定义得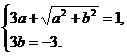 解得
解得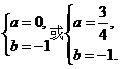 。故
。故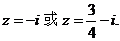
检验:若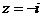 ,则原方程成立;若
,则原方程成立;若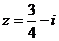 ,则原方程不成立。
,则原方程不成立。
故原方程有且只有一解z=-i.
4、估算检验。当解题过程是否等价变形难以把握时,可用估算的方法进行检验,以避免忽视充要条件而产生逻辑性错误。
例21、不等式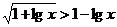 的解是 。
的解是 。
错解:两边平行得 ,即
,即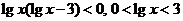 ,解得
,解得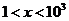 。
。
检验:先求定义域得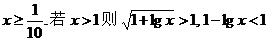 ,原不等式成立;若
,原不等式成立;若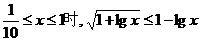 ,原不等式不成立,故正确答案为x>1。
,原不等式不成立,故正确答案为x>1。
5、作图检验。当问题具有几何背景时,可通过作图进行检验,以避免一些脱离事实而主观臆断致错。
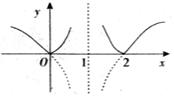 例22、函数
例22、函数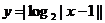 的递增区间是 。
的递增区间是 。
错解: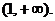
检验:由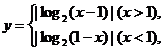
作图可知正确答案为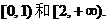
6、变法检验。一种方法解答之后,再用其它方法解之,看它们的结果是否一致,从而可避免方法单一造成的策略性错误。
例23、若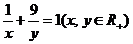 ,则
,则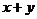 的最小值是 。
的最小值是 。
错解: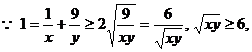
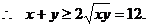
检验:上述错解在于两次使用重要不等式,等号不可能同时取到。
换一种解法为:
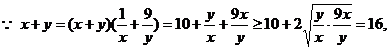

7、极端检验。当难以确定端点处是否成立时,可直接取其端点进行检验,以避免考虑不周全的错误。
例24、已知关于x的不等式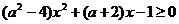 的解集是空集,求实数a的取值范围 。
的解集是空集,求实数a的取值范围 。
错解:由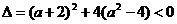 ,解得
,解得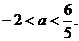
检验:若a=-2,则原不等式为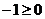 ,解集是空集,满足题意;若
,解集是空集,满足题意;若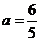 ,则原不等式为
,则原不等式为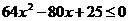 ,即
,即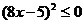 ,解得
,解得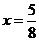 ,不满足题意。
,不满足题意。
故正确答案为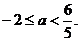
切记:解填空题应方法恰当,争取一步到位,答题形式标准,避免丢三落四,“一知半解”。
(一)数学填空题的解题方法
1、直接法:直接从题设条件出发,利用定义、性质、定理、公式等,经过变形、推理、计算、判断得到结论的,称为直接法。它是解填空题的最基本、最常用的方法。使用直接法解填空题,要善于通过现象看本质,自觉地、有意识地采取灵活、简捷的解法。
例1、乒乓球队的10名队员中有3名主力队员,派5名参加比赛。3名主力队员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四位置,那么不同的出场安排共有_________种(用数字作答)。
解:三名主力队员的排法有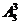 种,其余7名队员选2名安排在第二、四位置上有
种,其余7名队员选2名安排在第二、四位置上有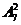 种排法,故共有排法数
种排法,故共有排法数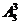
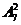 =252种。
=252种。
例2、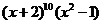 的展开式中
的展开式中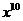 的系数为
。
的系数为
。
解: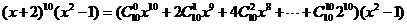
得展开式中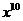 的系数为
的系数为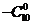
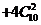 =179。
=179。
例3、已知函数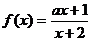 在区间
在区间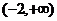 上为增函数,则实数
上为增函数,则实数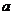 的取值范围是 。
的取值范围是 。
解: ,由复合函数的增减性可知,
,由复合函数的增减性可知,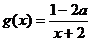 在
在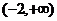 上为增函数,∴
上为增函数,∴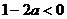 ,∴
,∴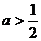 。
。
2、特殊化法:当填空题已知条件中含有某些不确定的量,但填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时,可以将题中变化的不定量选取一些符合条件的恰当特殊值(或特殊函数,或特殊角,特殊数列,图形特殊位置,特殊点,特殊方程,特殊模型等)进行处理,从而得出探求的结论。这样可大大地简化推理、论证的过程。
例4、在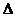 ABC中,角A、B、C所对的边分别为a、b、c,如果a、b、c成等差数列,则
ABC中,角A、B、C所对的边分别为a、b、c,如果a、b、c成等差数列,则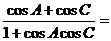
解法一:取特殊值a=3, b=4, c=5 ,则cosA=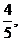 cosC=0,
cosC=0, 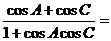
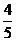 。
。
解法二:取特殊角A=B=C=600 cosA=cosC=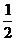 ,
,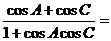
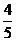 。
。
例5、如果函数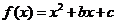 对任意实数
对任意实数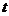 都有
都有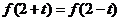 ,那么
,那么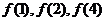 的大小关系是 。
的大小关系是 。
解:由于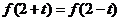 ,故知
,故知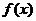 的对称轴是
的对称轴是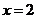 。可取特殊函数
。可取特殊函数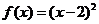 ,即可求得
,即可求得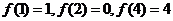 。∴
。∴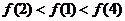 。
。
例6、已知SA,SB,SC两两所成角均为60°,则平面SAB与平面SAC所成的二面角为 。
解:取SA=SB=SC,则在正四面体S-ABC中,易得平面SAB与平面SAC所成的二面角为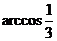 。
。
 例7、已知
例7、已知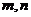 是直线,
是直线,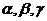 是平面,给出下列命题:①若
是平面,给出下列命题:①若 ,则
,则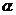 ∥
∥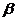 ;②若
;②若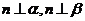 ,则
,则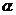 ∥
∥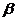 ;③若
;③若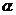 内不共线的三点到
内不共线的三点到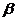 的距离都相等,则
的距离都相等,则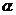 ∥
∥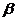 ;④若
;④若 ,且
,且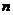 ∥
∥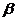 ,
,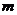 ∥
∥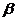 ,则
,则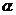 ∥
∥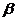 ;⑤若
;⑤若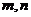 为异面直线,
为异面直线,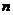
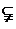
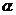 ,
,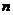 ∥
∥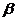 ,
,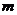
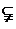
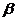 ,
,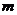 ∥
∥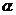 ,则
,则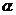 ∥
∥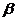 。则其中正确的命题是 。(把你认为正确的命题序号都填上)
。则其中正确的命题是 。(把你认为正确的命题序号都填上)
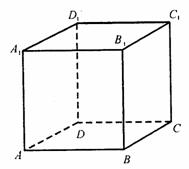
解:依题意可取特殊模型正方体AC1(如图),在正方体AC1中逐一判断各命题,易得正确的命题是②⑤。
3、数形结合法:对于一些含有几何背景的填空题,若能根据题目条件的特点,作出符合题意的图形,做到数中思形,以形助数,并通过对图形的直观分析、判断,则往往可以简捷地得出正确的结果。
例8、已知向量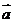 =
=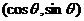 ,向量
,向量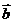 =
= ,则|2
,则|2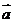 -
-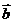 |的最大值是
|的最大值是
解:因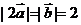 ,故向量2
,故向量2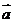 和
和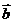 所对应的点A、B都在以原点为圆心,2为半径的圆上,从而|2
所对应的点A、B都在以原点为圆心,2为半径的圆上,从而|2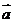 -
-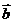 |的几何意义即表示弦AB的长,故|2
|的几何意义即表示弦AB的长,故|2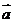 -
-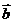 |的最大值为4。
|的最大值为4。
例9、如果不等式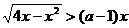 的解集为A,且
的解集为A,且 ,那么实数
,那么实数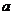 的取值范围是
。
的取值范围是
。
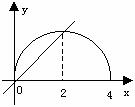 解:根据不等式解集的几何意义,作函数
解:根据不等式解集的几何意义,作函数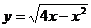 和
和
函数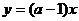 的图象(如图),从图上容易得出实数
的图象(如图),从图上容易得出实数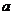 的取
的取
值范围是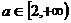 。
。
例10、设函数 f(x)=x3+ax2+2bx+c.若当 x∈(0,1)时,f(x)取得极大值;x∈(1,2)时,f(x)取得极小值,则 的取值范围是 .
 解:f´(x)= x2+ax+2b,令f´(x)=0,由条件知,上述方程应满足:一根在(0,1)之间,另一根在(1,2)之间,∴ ,得 ,在aob坐标系中,作出上述区域如图所示,而
的几何意义是过两点P(a,b)与A(1,2)的直线斜率,而P(a,b)在区域内,由图易知kPA∈(,1).
解:f´(x)= x2+ax+2b,令f´(x)=0,由条件知,上述方程应满足:一根在(0,1)之间,另一根在(1,2)之间,∴ ,得 ,在aob坐标系中,作出上述区域如图所示,而
的几何意义是过两点P(a,b)与A(1,2)的直线斜率,而P(a,b)在区域内,由图易知kPA∈(,1).
4、等价转化法:通过“化复杂为简单、化陌生为熟悉”将问题等价转化成便于解决的问题,从而得到正确的结果。
例11、不等式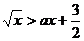 的解集为
的解集为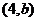 ,则
,则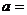 _______,
_______,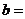 ________。
________。
解:设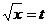 ,则原不等式可转化为:
,则原不等式可转化为: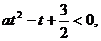 ∴a > 0,且2与
∴a > 0,且2与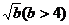 是方程
是方程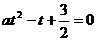 的两根,由此可得:
的两根,由此可得: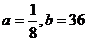 。
。
例12、不论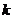 为何实数,直线
为何实数,直线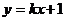 与圆
与圆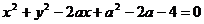 恒有交点,则实数
恒有交点,则实数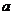 的取值范围是 。
的取值范围是 。
解:题设条件等价于点(0,1)在圆内或圆上,或等价于点(0,1)到圆 ,∴
,∴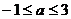 。
。
5、构造法:根据题设条件与结论的特殊性,构造出一些新的数学形式,并借助于它认识和解决问题的一种方法。
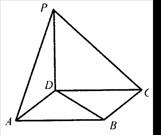 例13、如图,点P在正方形ABCD所在的平面外,PD⊥ABCD,PD=AD,则PA与BD所成角的度数为 。
例13、如图,点P在正方形ABCD所在的平面外,PD⊥ABCD,PD=AD,则PA与BD所成角的度数为 。
解:根据题意可将此图补形成一正方体,在正方体中易求得PA与BD所成角为60°。
例14、4个不同的小球放入编号为1,2,3,4的4个盒中,则只有1个空盒的放法共有 种(用数字作答)。
解:符合条件的放法是:有一个盒中放2个球,有2个盒中各放1个球。因此可先将球分成3堆(一堆2个,其余2堆各1个,即构造了球的“堆”),然后从4个盒中选出3个盒放3堆球,依分步计算原理,符合条件的放法有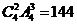 (种)。
(种)。
例15、椭圆 的焦点F1、F2,点P是椭圆上动点,当∠F1PF2为钝角时,点P的横坐标的取值范围是
 解:构造圆x2+y2=5,与椭圆 联立求得交点x02 =
解:构造圆x2+y2=5,与椭圆 联立求得交点x02 = 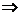 x0∈(- ,)
x0∈(- ,)
6、分析法:根据题设条件的特征进行观察、分析,从而得出正确的结论。
例16、如右图,在直四棱柱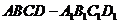 中,当底面四边形满足条件
时,有
中,当底面四边形满足条件
时,有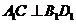 (填上你认为正确的一个条件
(填上你认为正确的一个条件
即可,不必考虑所有可能性的情形)。
解:因四棱柱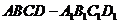 为直四棱柱,故
为直四棱柱,故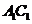 为
为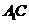 在面
在面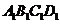 上的射影,从而要使
上的射影,从而要使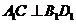 ,只要
,只要 与
与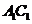 垂直,故底面四边形
垂直,故底面四边形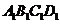 只要满足条件
只要满足条件
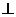
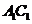 即可。
即可。
例17、以双曲线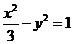 的左焦点F,左准线l为相应的焦点和准线的椭圆截直线
的左焦点F,左准线l为相应的焦点和准线的椭圆截直线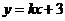 所得的弦恰好被x轴平分,则k的取值范围是
。
所得的弦恰好被x轴平分,则k的取值范围是
。
解:左焦点F为(-2,0),左准线l:x =-,因椭圆截直线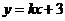 所得的弦恰好被x轴平分,故根据椭圆的对称性知,椭圆的中心即为直线
所得的弦恰好被x轴平分,故根据椭圆的对称性知,椭圆的中心即为直线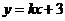 与x轴的交点
与x轴的交点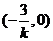 ,由
,由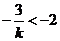 ,得0 < k < 。
,得0 < k < 。
数学填空题在前几年江苏高考中题量一直为4题,从去年开始增加到6题,今年虽然保持不变,仍为6题,但分值增加,由原来的每题4分增加到每题5分,在高考数学试卷中占分达到了20%。它和选择题同属客观性试题,它们有许多共同特点:其形态短小精悍、跨度大、知识覆盖面广、考查目标集中,形式灵活,答案简短、明确、具体,评分客观、公正、准确等。
根据填空时所填写的内容形式,可以将填空题分成两种类型:
一是定量型,要求考生填写数值、数集或数量关系,如:方程的解、不等式的解集、函数的定义域、值域、最大值或最小值、线段长度、角度大小等等。由于填空题和选择题相比,缺少选择支的信息,所以高考题中多数是以定量型问题出现。
二是定性型,要求填写的是具有某种性质的对象或者填写给定的数学对象的某种性质,如:给定二次曲线的准线方程、焦点坐标、离心率等等。近几年出现了定性型的具有多重选择性的填空题。
在解答填空题时,由于不反映过程,只要求结果,所以对正确性的要求比解答题更高、更严格,《考试说明》中对解答填空题提出的基本要求是“正确、合理、迅速”。为此在解填空题时要做到:快--运算要快,力戒小题大作;稳--变形要稳,不可操之过急;全--答案要全,力避残缺不齐;活--解题要活,不要生搬硬套;细--审题要细,不能粗心大意。
(四)考好数学的“四大绝招”
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com