
8.特殊角的三角函数值:
|
|
30° |
45° |
60° |
0° |
90° |
180° |
270° |
15° |
75° |
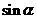 |
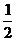 |
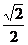 |
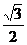 |
0 |
1 |
0 |
-1 |
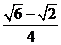 |
 |
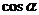 |
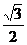 |
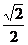 |
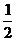 |
1 |
0 |
-1 |
0 |
 |
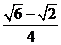 |
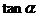 |
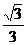 |
1 |
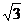 |
0 |
|
0 |
|
2-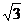 |
2+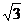 |
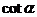 |
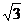 |
1 |
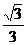 |
|
0 |
|
0 |
2+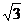 |
2-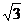 |
7.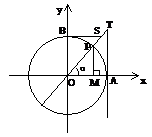 三角函数线的特征是:正弦线MP“站在
三角函数线的特征是:正弦线MP“站在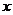 轴上(起点在
轴上(起点在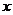 轴上)”、余弦线OM“躺在
轴上)”、余弦线OM“躺在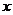 轴上(起点是原点)”、正切线AT“站在点
轴上(起点是原点)”、正切线AT“站在点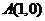 处(起点是
处(起点是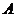 )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。如(1)若
)”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。如(1)若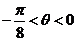 ,则
,则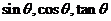 的大小关系为_____(答:
的大小关系为_____(答: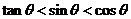 );(2)若
);(2)若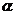 为锐角,则
为锐角,则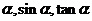 的大小关系为_______ (答:
的大小关系为_______ (答: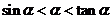 );(3)函数
);(3)函数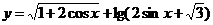 的定义域是_______(答:
的定义域是_______(答: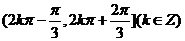 )
)
6、任意角的三角函数的定义:设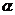 是任意一个角,P
是任意一个角,P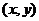 是
是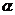 的终边上的任意一点(异于原点),它与原点的距离是
的终边上的任意一点(异于原点),它与原点的距离是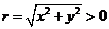 ,那么
,那么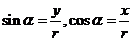 ,
,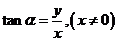 ,
,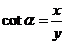
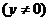 ,
,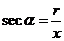
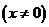 ,
,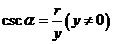 。三角函数值只与角的大小有关,而与终边上点P的位置无关。如(1)已知角
。三角函数值只与角的大小有关,而与终边上点P的位置无关。如(1)已知角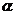 的终边经过点P(5,-12),则
的终边经过点P(5,-12),则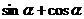 的值为__。(答:
的值为__。(答: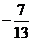 );(2)设
);(2)设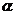 是第三、四象限角,
是第三、四象限角,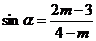 ,则
,则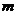 的取值范围是_______(答:(-1,
的取值范围是_______(答:(-1,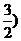 );(3)若
);(3)若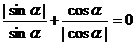 ,试判断
,试判断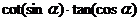 的符号(答:负)
的符号(答:负)
5.弧长公式: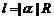 ,扇形面积公式:
,扇形面积公式: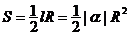 ,1弧度(1rad)
,1弧度(1rad)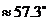 . 如已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。(答:2
. 如已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。(答:2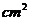 )
)
4、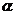 与
与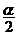 的终边关系:由“两等分各象限、一二三四”确定.如若
的终边关系:由“两等分各象限、一二三四”确定.如若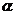 是第二象限角,则
是第二象限角,则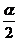 是第_____象限角(答:一、三)
是第_____象限角(答:一、三)
3. 终边相同的角的表示:
(1)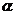 终边与
终边与 终边相同(
终边相同(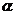 的终边在
的终边在 终边所在射线上)
终边所在射线上)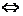
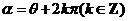 ,注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角
,注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角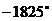 的终边相同,且绝对值最小的角的度数是___,合___弧度。(答:
的终边相同,且绝对值最小的角的度数是___,合___弧度。(答: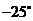 ;
;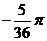 )
)
(2)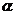 终边与
终边与 终边共线(
终边共线(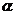 的终边在
的终边在 终边所在直线上)
终边所在直线上) 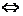
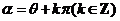 .
.
(3)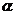 终边与
终边与 终边关于
终边关于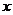 轴对称
轴对称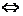
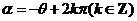 .
.
(4)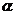 终边与
终边与 终边关于
终边关于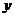 轴对称
轴对称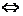
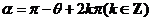 .
.
(5)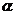 终边与
终边与 终边关于原点对称
终边关于原点对称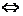
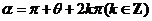 .
.
(6)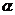 终边在
终边在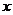 轴上的角可表示为:
轴上的角可表示为: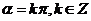 ;
;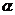 终边在
终边在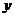 轴上的角可表示为:
轴上的角可表示为: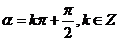 ;
;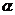 终边在坐标轴上的角可表示为:
终边在坐标轴上的角可表示为: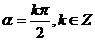 .如
.如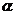 的终边与
的终边与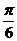 的终边关于直线
的终边关于直线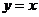 对称,则
对称,则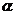 =____________。(答:
=____________。(答: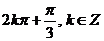 )
)
2、象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与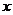 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。
轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。
1、角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。
8、函数的最大值和最小值:
(1)定义:函数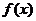 在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;函数
在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;函数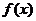 在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”。
在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”。
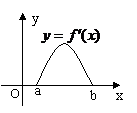 (2)求函数
(2)求函数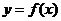 在[
在[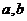 ]上的最大值与最小值的步骤:(1)求函数
]上的最大值与最小值的步骤:(1)求函数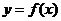 在(
在(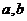 )内的极值(极大值或极小值);(2)将
)内的极值(极大值或极小值);(2)将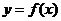 的各极值与
的各极值与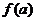 ,
,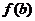 比较,其中最大的一个为最大值,最小的一个为最小值。如(1)函数
比较,其中最大的一个为最大值,最小的一个为最小值。如(1)函数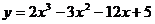 在[0,3]上的最大值、最小值分别是______(答:5;
在[0,3]上的最大值、最小值分别是______(答:5;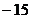 );(2)用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m。那么高为多少时容器的容积最大?并求出它的最大容积。(答:高为1.2米时,容积最大为
);(2)用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m。那么高为多少时容器的容积最大?并求出它的最大容积。(答:高为1.2米时,容积最大为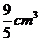 )
)
特别注意:(1)利用导数研究函数的单调性与最值(极值)时,要注意列表!(2)要善于应用函数的导数,考察函数单调性、最值(极值),研究函数的性态,数形结合解决方程不等式等相关问题。如(1)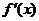 是
是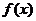 的导函数,
的导函数,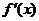 的图象如右图所示,则
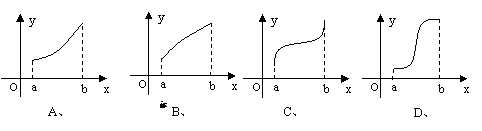
的图象如右图所示,则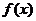 的图象只可能是
( 答:D )
的图象只可能是
( 答:D )
(2)方程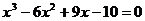 的实根的个数为______(答:1);(3)已知函数
的实根的个数为______(答:1);(3)已知函数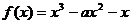 ,抛物线
,抛物线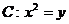 ,当
,当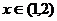 时,函数
时,函数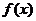 的图象在抛物线
的图象在抛物线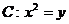 的上方,求
的上方,求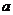 的取值范围(答:
的取值范围(答: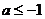 )。
)。
7、函数的极值:
(1)定义:设函数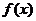 在点
在点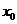 附近有定义,如果对
附近有定义,如果对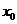 附近所有的点,都有
附近所有的点,都有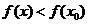 ,就说是
,就说是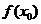 函数
函数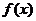 的一个极大值。记作
的一个极大值。记作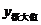 =
=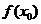 ,如果对
,如果对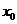 附近所有的点,都有
附近所有的点,都有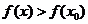 ,就说是
,就说是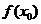 函数
函数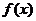 的一个极小值。记作
的一个极小值。记作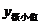 =
=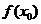 。极大值和极小值统称为极值。
。极大值和极小值统称为极值。
(2)求函数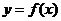 在某个区间上的极值的步骤:(i)求导数
在某个区间上的极值的步骤:(i)求导数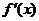 ;(ii)求方程
;(ii)求方程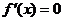 的根
的根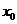 ;(iii)检查
;(iii)检查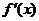 在方程
在方程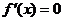 的根
的根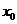 的左右的符号:“左正右负”
的左右的符号:“左正右负”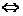
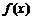 在
在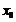 处取极大值;“左负右正”
处取极大值;“左负右正”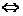
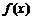 在
在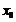 处取极小值。特别提醒:(1)
处取极小值。特别提醒:(1)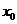 是极值点的充要条件是
是极值点的充要条件是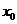 点两侧导数异号,而不仅是
点两侧导数异号,而不仅是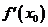 =0,
=0,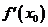 =0是
=0是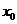 为极值点的必要而不充分条件。(2)给出函数极大(小)值的条件,一定要既考虑
为极值点的必要而不充分条件。(2)给出函数极大(小)值的条件,一定要既考虑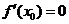 ,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记! 如(1)函数
,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记! 如(1)函数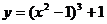 的极值点是 A、极大值点
的极值点是 A、极大值点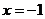 B、极大值点
B、极大值点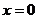 C、极小值点
C、极小值点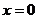 D、极小值点
D、极小值点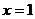 (答:C);(2)已知函数
(答:C);(2)已知函数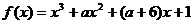 有极大值和极小值,则实数
有极大值和极小值,则实数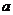 的取值范围是_____(答:
的取值范围是_____(答: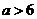 或
或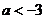 );(3)函数
);(3)函数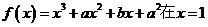 处有极小值10,则a+b的值为____(答:-7);(4)已知函数
处有极小值10,则a+b的值为____(答:-7);(4)已知函数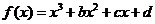 在区间[-1,2
]上是减函数,那么b+c有最___值___(答:大,
在区间[-1,2
]上是减函数,那么b+c有最___值___(答:大,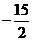 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com