
1.导数是从众多实际问题中抽象出来的一个重要的数学概念,要从它的几何意义和物理意义来对这一概念加以认识,才能把握其实质;
3.可导函数的四则运算法则
法则1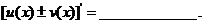 (口诀:和与差的导数等于导数的和与差).
(口诀:和与差的导数等于导数的和与差).
法则2 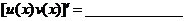 .(口诀:前导后不导,后导前不导,中间是正号)
.(口诀:前导后不导,后导前不导,中间是正号)
法则3  (口诀:分母平方要记牢,上导下不导,下导上不导,中间是负号)
(口诀:分母平方要记牢,上导下不导,下导上不导,中间是负号)
[特别提醒]
2.几种常见函数的导数
(1) 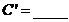 (C为常数);(2)
(C为常数);(2)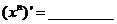 ,
n∈N+;(3)
,
n∈N+;(3)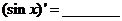 ;
;
(4)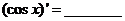 ; (5)
; (5)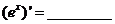 ; (6)
; (6) ;
;
(7)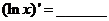 ; (8)
; (8) 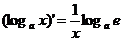 .
.
1. 导数的概念
(1)如果当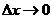 时,
时,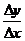 有极限,就说函数
有极限,就说函数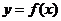 在点
在点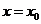 处存在导数,并将这个极限叫做函数
处存在导数,并将这个极限叫做函数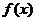 在点
在点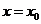 处的导数(或变化率),记作
处的导数(或变化率),记作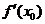 或
或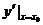 ,即
,即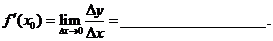
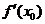 的几何意义是曲线
的几何意义是曲线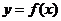 在点
在点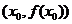 处的
;瞬时速度就是位移函数
处的
;瞬时速度就是位移函数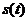 对
的导数;加速度就是速度函数
对
的导数;加速度就是速度函数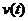 对______________的导数.
对______________的导数.
(2)如果函数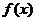 在开区间
在开区间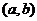 内的每一点都可导,其导数值在
内的每一点都可导,其导数值在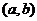 内构成一个新函数,这个函数叫做
内构成一个新函数,这个函数叫做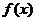 在开区间
在开区间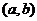 内的导函数,记作 或
.
内的导函数,记作 或
.
5.定积分与微积分基本定理
① 了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念.
② 了解微积分基本定理的含义.
[命题展望]
导数是高中数学的一个重要内容,导数的本身已经成为解决数学问题的重要工具,不论是研究函数的性质,还是解决不等式的证明问题和方程根的判断问题,还是解决曲线的切线问题,导数都发挥着非常重要的作用,所以在最近几年的高考试题中,对导数的考查逐步加强,从题量和题目的难度上都有了很大的提高,在全国各地的高考试卷中都有关于导数的试题。对导数的考查形式是多种多样,难易均有,可以在选择题与填空题中出现,主要考查导数的运算、导数的几何意义,导数的应用(主要研究函数的单调性、极值与最值等);也可以在解答题中出现,有时候作为压轴题,这时主要考查导数的综合应用,往往与函数、方程、数列、解析几何等联系在一起。
定积分是本章的另一个重要的概念,它可以看作是导数在某一区间上的逆运算。它是新课标新增加的内容之一,在以前的课本中没有出现定积分的概念,但随着新课标的实施与教育工作者对校本研究工作的开展,相信在2008年的高考试题中应该有所体现。
第一讲 导数及其运算
[知识梳理]
[知识盘点]
4.生活中的优化问题.
会利用导数解决某些实际问题..
3.导数在研究函数中的应用
① 了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间,对多项式函数一般不超过三次.
② 了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值,对多项式函数一般不超过三次;会求闭区间上函数的最大值、最小值,对多项式函数一般不超过三次.
2.导数的运算
① 能根据导数定义,求函数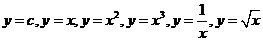 的导数.
的导数.
② 能利用表1给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,能求简单的复合函数(仅限于形如f(ax+b))的导数.
表1:常见基本初等函数的导数公式和常用导数运算公式:
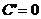 (C为常数);
(C为常数);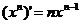 ,
n∈N+;
,
n∈N+;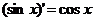 ;
;
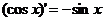 ;
;
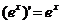 ;
; 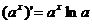 ;
; 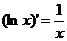 ;
; 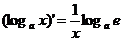 .
.
法则1 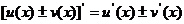 .
.
法则2 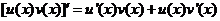 .
.
法则3 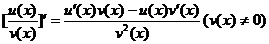 .
.
1.导数概念及其几何意义
① 了解导数概念的实际背景.
② 理解导数的几何意义.
8. The world ______ is made up of matter.
A. in that we live B. on which we live C. where we live in D. we live in
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com