
6.将一个物体竖直上抛,设经过时间t s后,物体上升的高度为s=10t-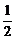 gt2,物体在1 s时的瞬时加速度为___ _m/s2.
gt2,物体在1 s时的瞬时加速度为___ _m/s2.
[典例精析]
例1.(1)设函数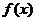 在
在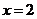 处可导,且
处可导,且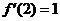 ,求
,求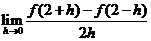 ;
;
(2)已知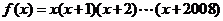 ,求
,求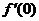 .
.
[剖析]利用导数的定义,可容易求得。
[解](1)由已知条件和导数的定义,可得: 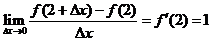 ,
,
当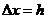 时,
时,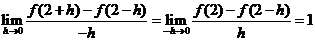
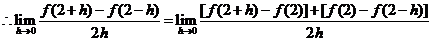
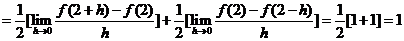 .
.
(2)解法一: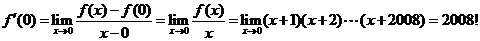
解法二:令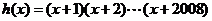 ,则
,则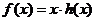
从而由导数乘法的计算公式得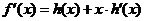
所以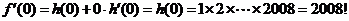
[警示](1)在对导数的定义理解时,要注意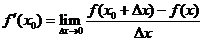 中
中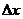 的形式变化,本例中就有
的形式变化,本例中就有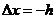 的情形出现;
的情形出现;
(2)设函数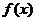 在
在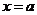 处可导,则
处可导,则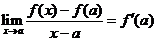 ,此结果作为导数定义的另一种形式,与导数的定义无关.我们可以证明之:令
,此结果作为导数定义的另一种形式,与导数的定义无关.我们可以证明之:令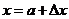 ,则当
,则当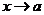 时,
时,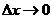 ,
, ;
;
(3)本例中的第(2)题充分说明了应用导数概念解题的方法与重要性,在复习时应给予重视。
[变式训练]:
5.过点P(-1,2)且与曲线y=3x2-4x+2在点M(1,1)处的切线平行的直线方程是______.
4.一质点做直线运动,由始点起经过ts后的距离为s=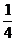 t4-4t3+16t2,则速度为零的时刻是(
)
t4-4t3+16t2,则速度为零的时刻是(
)
A.4s末 B.8s末 C.0s与8s末 D.0s,4s,8s末
3.(2006年安徽卷)若曲线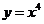 的一条切线
的一条切线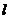 与直线
与直线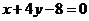 垂直,则
垂直,则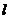 的方程为( )
的方程为( )
A.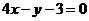 B.
B.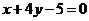 C.
C.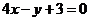 D.
D.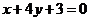
2.函数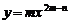 的导数为
的导数为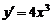 ,则 (
)
,则 (
)
A.m = 1,n = 2 B.m =-1,n=2 C.m =-1,n =-2 D.m =1,n =-2
1.某质点的运动方程是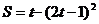 ,则在t=1s时的瞬时速度为 ( )
,则在t=1s时的瞬时速度为 ( )
A.-1 B.-3 C.7 D.13
5.复合函数的求导问题是个难点,要分清中间变量与复合关系,复合函数求导法则,像链条一样,必须一环一环套下去,而不能丢掉其中的一环. 防止漏掉一部分或漏掉符号造成错误.必须正确分析复合函数是由哪些基本函数经过怎样的顺序复合而成的,分清其间的复合关系.
[基础闯关]
4.对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用,在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误.
3.在对导数的概念进行理解时,特别要注意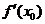 与
与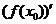 是不一样的,
是不一样的,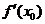 代表函数
代表函数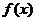 在
在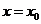 处的导数值,不一定为0 ;而
处的导数值,不一定为0 ;而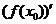 是函数值
是函数值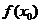 的导数,而函数值
的导数,而函数值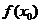 是一个常量,其导数一定为0,即
是一个常量,其导数一定为0,即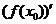 =0;
=0;
2.导数的概念及其运算是导数就用的基础,是高考考查的重点内容.考查方式多以客观题为主,主要考查求导数的基本公式和法则,以及导数的几何意义,也可以解答题的形式出现,即以导数的几何意义为背景设置成导数与解析几何的综合题;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com