
7.(2006年湖南卷)曲线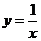 和
和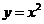 在它们交点处的两条切线与
在它们交点处的两条切线与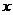 轴所围成的三角形面积是
.
轴所围成的三角形面积是
.
6.若函数y=x3-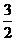 x2-a在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是 .
x2-a在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是 .
5.(2006年江西卷)对于R上可导的任意函数f(x),若满足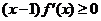 ,则必有( )
,则必有( )
A.f(0)+f(2)<2f(1) B. f(0)+f(2)£2f(1)
C. f(0)+f(2)³2f(1) D. f(0)+f(2)>2f(1)
4.(2007年山东泰安)已知a>0且a≠1,
f(x)=x2-a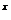 ,当x∈(-1,1)时,f(x)<
,当x∈(-1,1)时,f(x)<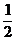 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.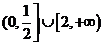 B.
B.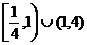 C.
C.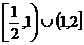 D.
D.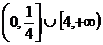
3.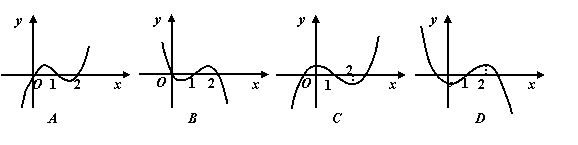 (2007年广东佛山)设
(2007年广东佛山)设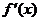 是函数
是函数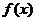 的导函数,
的导函数,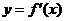 的图象如右图所示,则
的图象如右图所示,则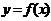 的图象最有可能的是( )
的图象最有可能的是( )
2.函数y=2x3-3x2-12x+5在[0,3]上的最大值与最小值分别是( )
 A .5 , -15 B.5 , 4 C. 5 ,-16 D. -4 ,-15
A .5 , -15 B.5 , 4 C. 5 ,-16 D. -4 ,-15
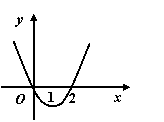
1.( 2006年湖南卷)设函数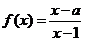 ,集合M=
,集合M=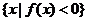 ,P=
,P=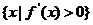 ,若M
,若M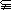 P,则实数a的取值范围是 ( )
P,则实数a的取值范围是 ( )
A.(-∞,1) B.(0,1) C.(1,+∞) D. [1,+∞)
6.(2007年山东莱山一中)设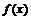 是定义在
是定义在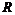 上的奇函数,且函数
上的奇函数,且函数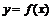 与
与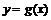 的图象关于直线
的图象关于直线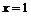 对称,当
对称,当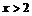 时,
时,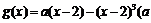 为常数)
为常数)
(1)求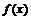 的解析式;
的解析式;
(2)若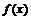 对区间
对区间 ,
, 上的每个
上的每个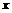 值,恒有
值,恒有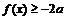 成立,求
成立,求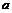 的取值范围。
的取值范围。
[能力提升]
5.已知函数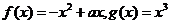 ,方程
,方程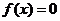 的一个根是6,
的一个根是6,
(1)若直线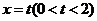 与函数
与函数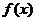 和
和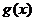 的图象的交点分别为
的图象的交点分别为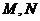 ,试求当
,试求当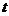 取何值时,线段
取何值时,线段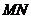 的长度取得最大值;
的长度取得最大值;
(2)函数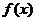 的图象在
的图象在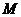 点处的切线为
点处的切线为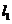 ,
,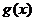 在
在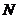 点处的切线为
点处的切线为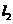 ,若
,若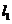 、
、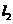 与
与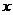 轴的交点分别为
轴的交点分别为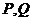 ,试求
,试求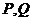 两点之间的距离的取值范围。
两点之间的距离的取值范围。
例6.已知函数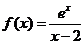 ,
,
(1)函数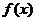 的单调区间;
的单调区间;
(2)求函数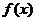 图象在与
图象在与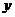 轴交点得的切线与两坐标轴所围成的图形的面积;
轴交点得的切线与两坐标轴所围成的图形的面积;
(3)判断方程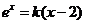 解的情况(
解的情况(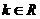 ).
).
[剖析]求函数的单调区间一般可以利用函数的导数来解决,即转化解不等式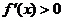 和
和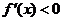 ;不等式的解集即为函数的单调区间,但首先要研究函数的定义域;求曲线在某一点的切线可以利用导数的几何意义;要研究方程根的个数问题,则可以通过函数图象与
;不等式的解集即为函数的单调区间,但首先要研究函数的定义域;求曲线在某一点的切线可以利用导数的几何意义;要研究方程根的个数问题,则可以通过函数图象与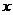 轴交点的数来分析,要画出函数大致图象,应函数的单调性、函数的极值及函数经过的特殊点等多个方面来考查.
轴交点的数来分析,要画出函数大致图象,应函数的单调性、函数的极值及函数经过的特殊点等多个方面来考查.
[解](1)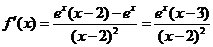 ,因为函数的定义域为
,因为函数的定义域为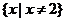 ,令
,令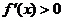 ,解得:
,解得: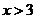 ;令
;令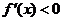 ,解得
,解得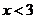 且
且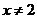 ,所以函数的单调递增区间是
,所以函数的单调递增区间是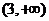 ,单调递减区间是
,单调递减区间是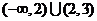 .
.
 (2)
(2) 与
与 轴的交点设为
轴的交点设为 ,则
,则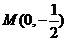 ,由于
,由于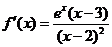 ,
,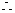 切线的斜率为
切线的斜率为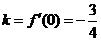 .
.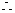 切线方程为
切线方程为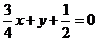 .
.
令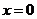 ,得
,得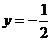 ,令
,令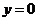 ,得
,得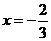 .
.
所以所围三角形的面积为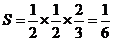 .
.
(3)方程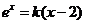 等价于
等价于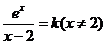 ,在平面直角坐标系中画出函数
,在平面直角坐标系中画出函数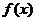 的图象,如右图所示:
的图象,如右图所示:
所以当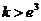 时,方程有2个根;当
时,方程有2个根;当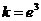 时,方程有1个根;当
时,方程有1个根;当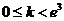 时,方程没有根;当
时,方程没有根;当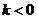 时,方程有1个根.
时,方程有1个根.
[警示]在近年的高考试题中,导数越来越成为一个考查热点,由于导数本身具有强大的工具作用,导数的单调性、极值、最值的研究,曲线切线问题的解决,不等式的证明、恒成立问题以方程根的讨论等问题中都具有着重要的作。以导数为载体的综合题已经成为了高考命题的风向标。利用导数不仅能够判断函数的单调性,研究函数的极值与最值情况,而且还能在此基础上画出函数的大致图象,得到函数图象与 轴交点的或两个函数的交点的条件,从而为研究方程的根及函数的零点提供方便,所以在解决方程的根的问题中,要善于运用导数的方法进行求解.
轴交点的或两个函数的交点的条件,从而为研究方程的根及函数的零点提供方便,所以在解决方程的根的问题中,要善于运用导数的方法进行求解.
[变式训练]
4.已知函数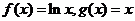
(1)若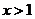 ,求证:
,求证: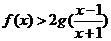 ;
;
(2)是否存在实数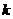 ,使得方程
,使得方程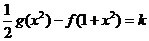 有四个不同的实数根?若存在,求出实数
有四个不同的实数根?若存在,求出实数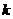 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
例5.(2007山东省样题)已知函数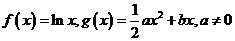
(Ⅰ)若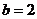 ,且
,且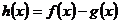 存在单调递减区间,求
存在单调递减区间,求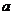 的取值范围;
的取值范围;
(Ⅱ)设函数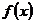 的图象C1与函数
的图象C1与函数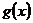 图象C1交于点P、Q,过线段PQ的中点作
图象C1交于点P、Q,过线段PQ的中点作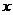 轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.
轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.
[剖析]利用导数的几何意义,函数在某一点处的导数值,就是函数图象在该点处的切线的斜率,求得切线的斜率后,再通过比较其在C1在点M处的切线与C2在点N处的切线的斜率不相等,来证明该题。
[解](I)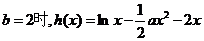 ,则
,则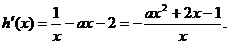
因为函数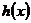 存在单调递减区间,所以
存在单调递减区间,所以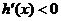 有解.
有解.
又因为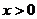 时,则
时,则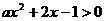 有
有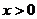 的解.
的解.
①当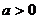 时,
时,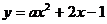 为开口向上的抛物线,
为开口向上的抛物线,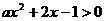 总有
总有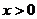 的解;
的解;
②当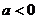 时,
时,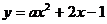 为开口向下的抛物线,而
为开口向下的抛物线,而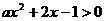 总有
总有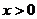 的解;
的解;
则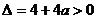 ,且方程
,且方程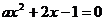 至少有一正根.此时,
至少有一正根.此时,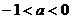
综上所述,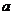 的取值范围为
的取值范围为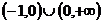 .
.
(II)证法一 设点P、Q的坐标分别是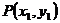 ,
,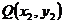 ,
,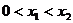 ,
,
则点M、N的横坐标为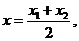 在C1点M处的切线斜率为
在C1点M处的切线斜率为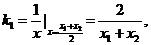
在C2点N处的切线斜率为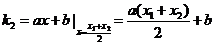
假设C1在点M处的切线与C2在点N处的切线平行,则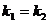 , 即
, 即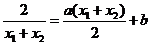 ,则
,则
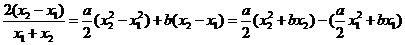 =
=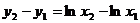
所以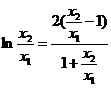 设
设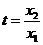 则
则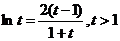 ①
①
令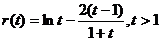 ,则
,则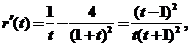
因为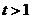 时,
时,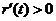 ,所以
,所以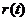 在
在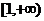 上单调递增. 故
上单调递增. 故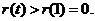
则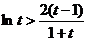 . 这与①矛盾,假设不成立.
. 这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
证法二:同证法一得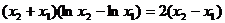
因为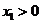 ,所以
,所以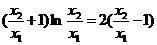 ,令
,令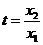 ,得
,得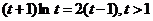 ②
②
令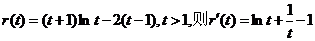
因为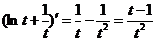 ,所以
,所以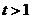 时,
时,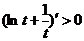 ,故
,故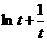 在
在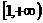 上单调递增.从而
上单调递增.从而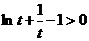 ,即
,即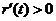 ,于是
,于是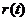 在
在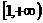 上单调递增.
上单调递增.
故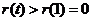 即
即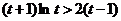 这与②矛盾,假设不成立.
这与②矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
[警示]利用导数求曲线的切线问题,几乎是每年必考的内容,这类问题,即有可能出现在选择题与填空题中,也有可能出现在解答题中。在这类问题中,导数所担负的任务是求出其切线的斜率,综合考察导数在解决函数单调性,函数曲线的切线等问题中的作用.
[变式训练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com