
3.(1)函数极值的概念
函数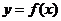 在点
在点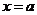 处的函数值
处的函数值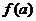 比它在点
比它在点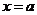 附近其它点的函数值都小,
附近其它点的函数值都小,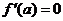 ;而且在点
;而且在点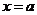 附近的左侧 ,右侧 ,则点
附近的左侧 ,右侧 ,则点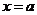 叫做函数
叫做函数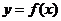 的 ,
的 ,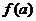 叫做函数
叫做函数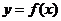 的 .
的 .
函数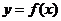 在点
在点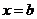 处的函数值
处的函数值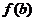 比它在点
比它在点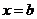 附近其它点的函数值都大,
附近其它点的函数值都大,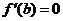 ;而且在点
;而且在点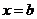 附近的左侧 ,右侧 ,则点
附近的左侧 ,右侧 ,则点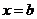 叫做函数
叫做函数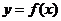 的 ,
的 ,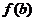 叫做函数
叫做函数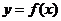 的 .
的 .
极小值点与极大值点统称为 ,极小值与极大值统称为 .
(2)求函数极值的步骤:
① ;② ;③ 。
2.如果一个函数在某个区间内的绝对值 ,那么函数在这个范围内变化 ,这时函数的图象就越“ ”。
1.函数的单调性
函数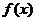 在某个区间
在某个区间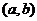 内,若
内,若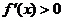 ,则
,则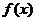 为 ;若
为 ;若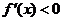 ,则
,则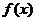 为 ;若
为 ;若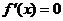 ,则
,则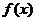 为 。
为 。
12. 已知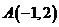 为抛物线
为抛物线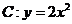 上的点,直线
上的点,直线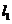 过点
过点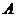 ,且与抛物线
,且与抛物线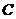 相切,直线
相切,直线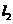 :
: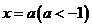 交抛物线
交抛物线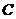 于点
于点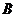 ,交直线
,交直线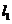 于点
于点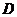 .
.
(1)求直线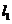 的方程;
的方程;
(2)求△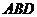 的面积
的面积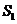 .
.
第二讲 导数的应用
[知识梳理]
[知识盘点]
11. 曲线y=x2+1上过点P的切线与曲线y=-2x2-1相切,求点P的坐标.
10.求函数的导数
(1)y=(x2-2x+3)e2x;
(2)y=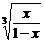 .
.
9.(2006年江苏卷)对正整数n,设曲线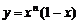 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为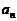 ,则数列
,则数列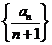 的前n项和的公式是
.
的前n项和的公式是
.
8.设曲线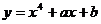 在x=1处的切线方程是
在x=1处的切线方程是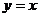 ,则
,则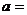 ,
,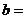 .
.
7.设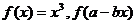 的导数是
.
的导数是
.
6.已知f(x)=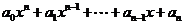 ,则
,则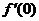 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com