
1.在实验室中,通常将金属钠保存在
A.水中 B. 煤油中 C. 四氯化碳中 D.汽油中
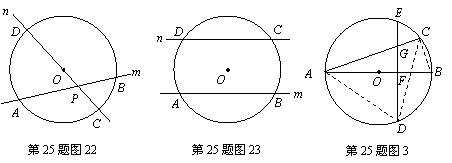
102.(08广东佛山25题)25.我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1) 如图1,在圆O所在平面上,放置一条直线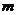 (
(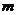 和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些(直接写出两个即可)?
和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些(直接写出两个即可)?
(2) 如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线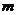 和
和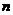 (
(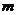 与圆O分别交于点A、B,
与圆O分别交于点A、B,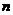 与圆O分别交于点C、D).
与圆O分别交于点C、D).
请你根据所构造的图形提出一个结论,并证明之.
(3) 如图3,其中AB是圆O的直径,AC是弦,D是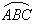
 的中点,弦DE⊥AB于点F.
请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.
请找出点C和点E重合的条件,并说明理由.
(08广东佛山25题解答)解:(1) 弦(图中线段AB)、弧(图中的ACB弧)、弓形、求弓形的面积(因为是封闭图形)等. (写对一个给1分,写对两个给2分)
(2) 情形1 如图21,AB为弦,CD为垂直于弦AB的直径. …………………………3分
结论:(垂径定理的结论之一). …………………………………………………………4分
证明:略(对照课本的证明过程给分). …………………………………………………7分
情形2 如图22,AB为弦,CD为弦,且AB与CD在圆内相交于点P.
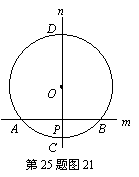 结论:
结论: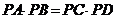 .
.
证明:略.
情形3 (图略)AB为弦,CD为弦,且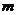 与
与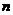 在圆外相交于点P.
在圆外相交于点P.
结论: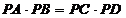 .
.
证明:略.
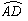
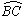 情形4 如图23,AB为弦,CD为弦,且AB∥CD.
情形4 如图23,AB为弦,CD为弦,且AB∥CD.
结论: = .
证明:略.
(上面四种情形中做一个即可,图1分,结论1分,证明3分;
其它正确的情形参照给分;若提出的是错误的结论,则需证明结论是错误的)
(3) 若点C和点E重合,
则由圆的对称性,知点C和点D关于直径AB对称. …………………………………8分
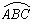 设
设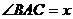 ,则
,则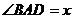 ,
,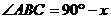 .………………………………9分
.………………………………9分
又D是 的中点,所以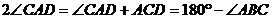 ,
,
即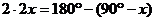 .………………………………………………………10分
.………………………………………………………10分
解得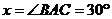 .……………………………………………………………11分
.……………………………………………………………11分
(若求得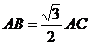 或
或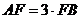 等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明)
等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明)
101.(08山东聊城25题)25.(本题满分12分)如图,把一张长10cm,宽8cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).

(1)要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;
(3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由.
(08山东聊城25题解答)(本题满分12分)
解:(1)设正方形的边长为 cm,则
cm,则
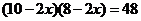 .························································································ 1分
.························································································ 1分
即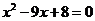 .
.
解得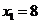 (不合题意,舍去),
(不合题意,舍去),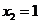 .
.
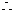 剪去的正方形的边长为1cm.·············································································· 3分
剪去的正方形的边长为1cm.·············································································· 3分
(注:通过观察、验证直接写出正确结果给3分)
(2)有侧面积最大的情况.
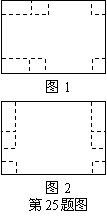 设正方形的边长为
设正方形的边长为 cm,盒子的侧面积为
cm,盒子的侧面积为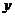 cm2,
cm2,
则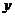 与
与 的函数关系式为:
的函数关系式为:
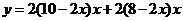 .
.
即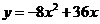 .······························································································· 5分
.······························································································· 5分
改写为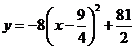 .
.
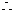 当
当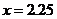 时,
时,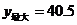 .
.
即当剪去的正方形的边长为2.25cm时,长方体盒子的侧面积最大为40.5cm2.········ 7分
(3)有侧面积最大的情况.
设正方形的边长为 cm,盒子的侧面积为
cm,盒子的侧面积为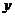 cm2.
cm2.
若按图1所示的方法剪折,则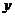 与
与 的函数关系式为:
的函数关系式为:
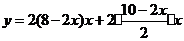 .
.
即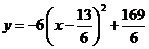 .
.
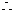 当
当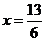 时,
时,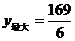 .····························· 9分
.····························· 9分
若按图2所示的方法剪折,则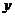 与
与 的函数关系式为:
的函数关系式为:
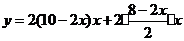 .
.
即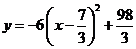 .
.
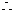 当
当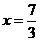 时,
时,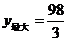 .················································································· 11分
.················································································· 11分
比较以上两种剪折方法可以看出,按图2所示的方法剪折得到的盒子侧面积最大,即当剪去的正方形的边长为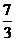 cm时,折成的有盖长方体盒子的侧面积最大,最大面积为
cm时,折成的有盖长方体盒子的侧面积最大,最大面积为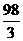 cm2.
cm2.
说明:解答题各小题只给了一种解答及评分说明,其他解法只要步骤合理,解答正确,均应给出相应分数.
100.(08广东梅州23题) 23.本题满分11分.
23.本题满分11分.
如图11所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为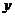 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L.
(3)若P是抛物线的对称轴L上的点,那么使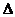 PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
(08广东梅州23题解答)解: (1) 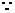 DC∥AB,AD=DC=CB,
DC∥AB,AD=DC=CB,
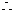 ∠CDB=∠CBD=∠DBA,··············································································· 0.5分
∠CDB=∠CBD=∠DBA,··············································································· 0.5分
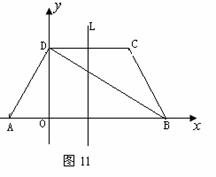 ∠DAB=∠CBA,
∠DAB=∠CBA, 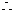 ∠DAB=2∠DBA, ············ 1分
∠DAB=2∠DBA, ············ 1分
∠DAB+∠DBA=90 ,
, 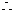 ∠DAB=60
∠DAB=60 , ·········· 1.5分
, ·········· 1.5分
∠DBA=30 ,
,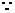 AB=4,
AB=4, 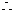 DC=AD=2,
········· 2分
DC=AD=2,
········· 2分
Rt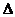 AOD,OA=1,OD=
AOD,OA=1,OD=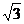 ,··························· 2.5分
,··························· 2.5分
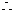 A(-1,0),D(0,
A(-1,0),D(0, 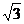 ),C(2,
),C(2, 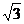 ). · 4分
). · 4分
(2)根据抛物线和等腰梯形的对称性知,满足条件的抛物线必过点A(-1,0),B(3,0),
故可设所求为 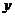 =
=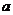 (
( +1)(
+1)(  -3) ······························································ 6分
-3) ······························································ 6分
将点D(0, 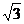 )的坐标代入上式得,
)的坐标代入上式得, 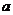 =
=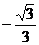 .
.
所求抛物线的解析式为 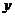 =
= ·········································· 7分
·········································· 7分
其对称轴L为直线 =1.······················································································ 8分
=1.······················································································ 8分
(3) 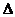 PDB为等腰三角形,有以下三种情况:
PDB为等腰三角形,有以下三种情况:
①因直线L与DB不平行,DB的垂直平分线与L仅有一个交点P1,P1D=P1B,
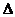 P1DB为等腰三角形; ················································································· 9分
P1DB为等腰三角形; ················································································· 9分
②因为以D为圆心,DB为半径的圆与直线L有两个交点P2、P3,DB=DP2,DB=DP3, 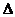 P2DB,
P2DB, 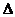 P3DB为等腰三角形;
P3DB为等腰三角形;
③与②同理,L上也有两个点P4、P5,使得 BD=BP4,BD=BP5. ···················· 10分
由于以上各点互不重合,所以在直线L上,使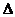 PDB为等腰三角形的点P有5个.
PDB为等腰三角形的点P有5个.
99.(08福建南平26题)26.(14分)
(1)如图1,图2,图3,在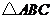 中,分别以
中,分别以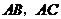 为边,向
为边,向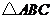 外作正三角形,正四边形,正五边形,
外作正三角形,正四边形,正五边形,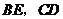 相交于点
相交于点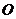 .
.
①如图1,求证: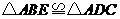 ;
;
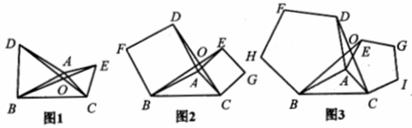
②探究:如图1,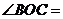
 ;
;
如图2,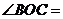
 ;
;
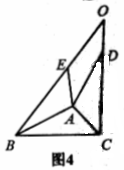 如图3,
如图3,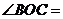
 .
.
(2)如图4,已知: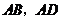 是以
是以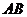 为边向
为边向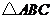 外所作正
外所作正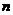 边形的一组邻边;
边形的一组邻边;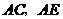 是以
是以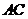 为边向
为边向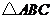 外所作正
外所作正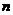 边形的一组邻边.
边形的一组邻边.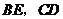 的延长相交于点
的延长相交于点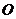 .
.
①猜想:如图4,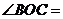
 (用含
(用含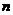 的式子表示);
的式子表示);
②根据图4证明你的猜想.
(08福建南平26题解答)(1)①证法一: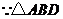 与
与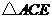 均为等边三角形,
均为等边三角形,
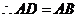 ,
,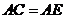 ························································································ 2分
························································································ 2分
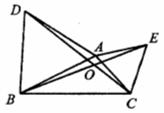 且
且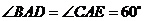 ··············································· 3分
··············································· 3分
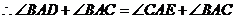 ,
,
即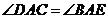 ························································ 4分
························································ 4分
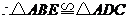 .··················································· 5分
.··················································· 5分
证法二: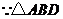 与
与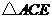 均为等边三角形,
均为等边三角形,
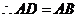 ,
,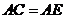 ························································································ 2分
························································································ 2分
且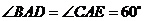 ························································································ 3分
························································································ 3分
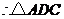 可由
可由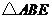 绕着点
绕着点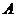 按顺时针方向旋转
按顺时针方向旋转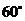 得到··································· 4分
得到··································· 4分
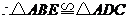 .··························································································· 5分
.··························································································· 5分
②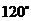 ,
,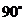 ,
,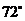 .········································································ 8分(每空1分)
.········································································ 8分(每空1分)
(2)①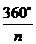 ········································································································ 10分
········································································································ 10分
②证法一:依题意,知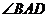 和
和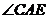 都是正
都是正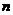 边形的内角,
边形的内角,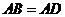 ,
,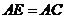 ,
,
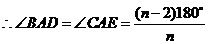
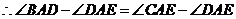 ,即
,即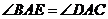 .····························· 11分
.····························· 11分
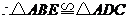 .·························································································· 12分
.·························································································· 12分
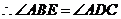 ,
,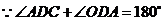 ,
,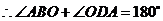 ······ 13分
······ 13分
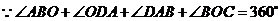 ,
,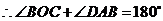
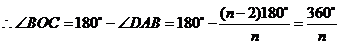 ········································ 14分
········································ 14分
证法二:同上可证 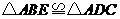 .··························································· 12分
.··························································· 12分
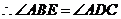 ,如图,延长
,如图,延长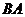 交
交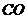 于
于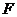 ,
,
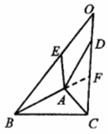
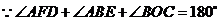 ,
,
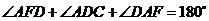 ································ 13分
································ 13分
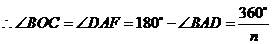 ················· 14分
················· 14分
证法三:同上可证 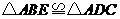 .··························································· 12分
.··························································· 12分
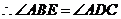 .
.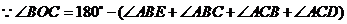
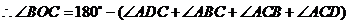
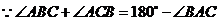 ,
,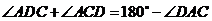
 ························································ 13分
························································ 13分
即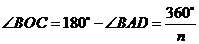 ········································································ 14分
········································································ 14分
证法四:同上可证 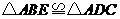 .··························································· 12分
.··························································· 12分
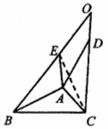
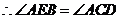 .如图,连接
.如图,连接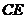 ,
,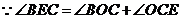
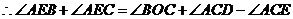
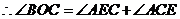 .···································· 13分
.···································· 13分
即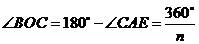 ······························· 14分
······························· 14分
注意:此题还有其它证法,可相应评分.
98.(08四川资阳24题)24.(本小题满分12分)
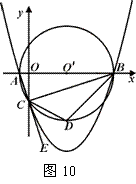 如图10,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
如图10,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.
(08四川资阳24题解答)(1) ∵以AB为直径作⊙O′,交y轴的负半轴于点C,
∴∠OCA+∠OCB=90°,
又∵∠OCB+∠OBC=90°,
∴∠OCA=∠OBC,
又∵∠AOC= ∠COB=90°,
∴ΔAOC∽ ΔCOB,························································································ 1分
∴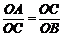 .
.
又∵A(–1,0),B(9,0),
∴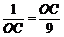 ,解得OC=3(负值舍去).
,解得OC=3(负值舍去).
∴C(0,–3),
······················································································································ 3分
设抛物线解析式为y=a(x+1)(x–9),
∴–3=a(0+1)(0–9),解得a=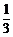 ,
,
∴二次函数的解析式为y=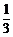 (x+1)(x–9),即y=
(x+1)(x–9),即y=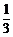 x2–
x2–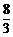 x–3.···························· 4分
x–3.···························· 4分
(2) ∵AB为O′的直径,且A(–1,0),B(9,0),
∴OO′=4,O′(4,0),····················································································· 5分
∵点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,
∴∠BCD=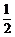 ∠BCE=
∠BCE=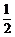 ×90°=45°,
×90°=45°,
连结O′D交BC于点M,则∠BO′D=2∠BCD=2×45°=90°,OO′=4,O′D=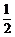 AB=5.
AB=5.
∴D(4,–5).································································································· 6分
 ∴设直线BD的解析式为y=kx+b(k≠0)
∴设直线BD的解析式为y=kx+b(k≠0)
∴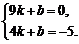 ··························································· 7分
··························································· 7分
解得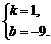
∴直线BD的解析式为y=x–9.····································· 8分
(3) 假设在抛物线上存在点P,使得∠PDB=∠CBD,
解法一:设射线DP交⊙O′于点Q,则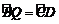 .
.
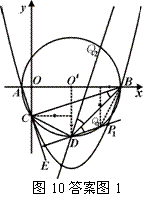
分两种情况(如答案图1所示):
①∵O′(4,0),D(4,–5),B(9,0),C(0,–3).
∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,
因此,点Q1(7,–4)符合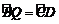 ,
,
∵D(4,–5),Q1(7,–4),
∴用待定系数法可求出直线DQ1解析式为y=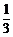 x–
x–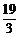 .··································· 9分
.··································· 9分
解方程组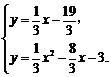 得
得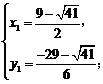
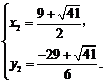
∴点P1坐标为(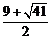 ,
,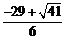 ),[坐标为(
),[坐标为(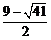 ,
,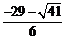 )不符合题意,舍去].
)不符合题意,舍去].
······················································································································ 10分
②∵Q1(7,–4),
∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合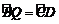 .
.
∵D(4,–5),Q2(7,4).
∴用待定系数法可求出直线DQ2解析式为y=3x–17.······································ 11分
解方程组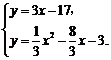 得
得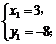
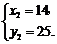
∴点P2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去].
······················································································································ 12分
∴符合条件的点P有两个:P1(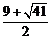 ,
,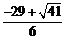 ),P2(14,25).
),P2(14,25).
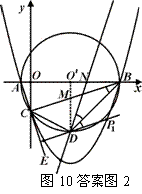 解法二:分两种情况(如答案图2所示):
解法二:分两种情况(如答案图2所示):
①当DP1∥CB时,能使∠PDB=∠CBD.
∵B(9,0),C(0,–3).
∴用待定系数法可求出直线BC解析式为y=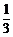 x–3.
x–3.
又∵DP1∥CB,∴设直线DP1的解析式为y=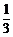 x+n.
x+n.
把D(4,–5)代入可求n=
–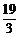 ,
,
∴直线DP1解析式为y=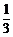 x–
x–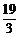 .························· 9分
.························· 9分
解方程组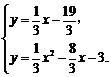 得
得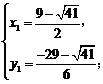
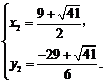
∴点P1坐标为(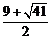 ,
,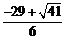 ),[坐标为(
),[坐标为(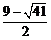 ,
,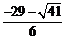 )不符合题意,舍去].
)不符合题意,舍去].
······················································································································ 10分
②在线段O′B上取一点N,使BN=DM时,得ΔNBD≌ΔMDB(SAS),∴∠NDB=∠CBD.
由①知,直线BC解析式为y=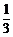 x–3.
x–3.
取x=4,得y= –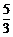 ,∴M(4,–
,∴M(4,–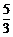 ),∴O′N=O′M=
),∴O′N=O′M=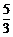 ,∴N(
,∴N(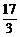 ,0),
,0),
又∵D(4,–5),
∴直线DN解析式为y=3x–17.······································································ 11分
解方程组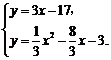 得
得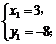
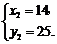
∴点P2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去].
······················································································································ 12分
∴符合条件的点P有两个:P1(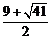 ,
,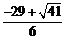 ),P2(14,25).
),P2(14,25).
解法三:分两种情况(如答案图3所示):
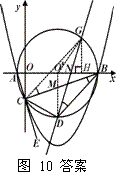 ①求点P1坐标同解法二.··············································································· 10分
①求点P1坐标同解法二.··············································································· 10分
②过C点作BD的平行线,交圆O′于G,
此时,∠GDB=∠GCB=∠CBD.
由(2)题知直线BD的解析式为y=x–9,
又∵ C(0,–3)
∴可求得CG的解析式为y=x–3,
设G(m,m–3),作GH⊥x轴交与x轴与H,
连结O′G,在Rt△O′GH中,利用勾股定理可得,m=7,
由D(4,–5)与G(7,4)可得,
DG的解析式为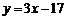 ,··········································································· 11分
,··········································································· 11分
解方程组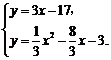 得
得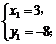
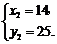
∴点P2坐标为(14,25),[坐标为(3,–8)不符合题意,舍去].························ 12分
∴符合条件的点P有两个:P1(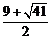 ,
,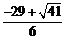 ),P2(14,25).
),P2(14,25).
说明:本题解法较多,如有不同的正确解法,请按此步骤给分.
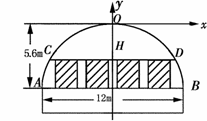
97.(08新疆自治区24题)(10分)某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.
(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户?
 (08新疆自治区24题解析)24.(10分)解:(1)设抛物线的表达式为
(08新疆自治区24题解析)24.(10分)解:(1)设抛物线的表达式为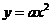 1分
1分
点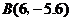 在抛物线的图象上.
在抛物线的图象上.
∴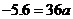
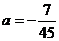 ······························································ 3分
······························································ 3分
∴抛物线的表达式为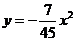 ············································································· 4分
············································································· 4分
(2)设窗户上边所在直线交抛物线于C、D两点,D点坐标为(k,t)
已知窗户高1.6m,∴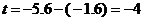 ··························································· 5分
··························································· 5分
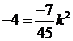
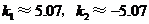 (舍去)············································································ 6分
(舍去)············································································ 6分
∴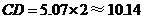 (m)·············································································· 7分
(m)·············································································· 7分
又设最多可安装n扇窗户
∴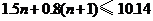 ····················································································· 9分
····················································································· 9分
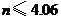 .
.
答:最多可安装4扇窗户.···················································································· 10分
(本题不要求学生画出4个表示窗户的小矩形
96.(08四川自贡26题)抛物线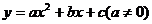 的顶点为M,与
的顶点为M,与 轴的交点为A、B(点B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于
轴的交点为A、B(点B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于 的一元二次方程
的一元二次方程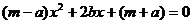 有两个相等的实数根。
有两个相等的实数根。
(1)判断△ABM的形状,并说明理由。
(2)当顶点M的坐标为(-2,-1)时,求抛物线的解析式,并画出该抛物线的大致图形。
(3)若平行于 轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与
轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与 轴相切,求该圆的圆心坐标。
轴相切,求该圆的圆心坐标。
(08四川自贡26题解析)解:(1)令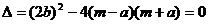
得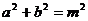
由勾股定理的逆定理和抛物线的对称性知
△ABM是一个以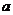 、
、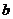 为直角边的等腰直角三角形
为直角边的等腰直角三角形
(2)设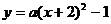
∵△ABM是等腰直角三角形
∴斜边上的中线等于斜边的一半
又顶点M(-2,-1)
∴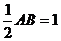 ,即AB=2
,即AB=2
∴A(-3,0),B(-1,0)
将B(-1,0) 代入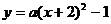 中得
中得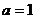
∴抛物线的解析式为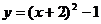 ,即
,即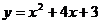
图略
(3)设平行于 轴的直线为
轴的直线为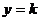
解方程组错误!不能通过编辑域代码创建对象。
得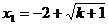 ,
,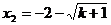 (
(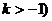
∴线段CD的长为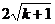
∵以CD为直径的圆与 轴相切
轴相切
据题意得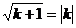
∴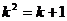
解得 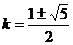
∴圆心坐标为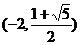 和
和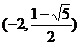
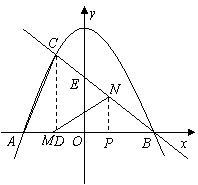
95.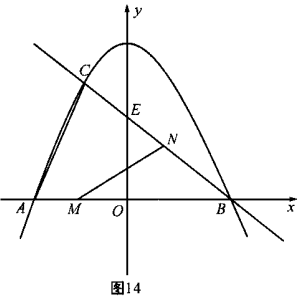 (08四川巴中30题)(12分)30.已知:如图14,抛物线
(08四川巴中30题)(12分)30.已知:如图14,抛物线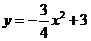 与
与 轴交于点
轴交于点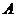 ,点
,点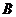 ,与直线
,与直线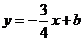 相交于点
相交于点 ,点
,点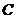 ,直线
,直线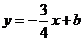 与
与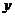 轴交于点
轴交于点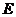 .
.
(1)写出直线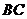 的解析式.
的解析式.
(2)求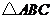 的面积.
的面积.
(3)若点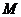 在线段
在线段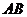 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从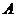 向
向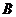 运动(不与
运动(不与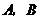 重合),同时,点
重合),同时,点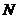 在射线
在射线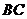 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从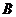 向
向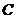 运动.设运动时间为
运动.设运动时间为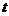 秒,请写出
秒,请写出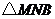 的面积
的面积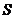 与
与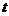 的函数关系式,并求出点
的函数关系式,并求出点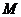 运动多少时间时,
运动多少时间时,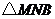 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
 (08四川巴中30题解析)解:(1)在
(08四川巴中30题解析)解:(1)在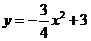 中,令
中,令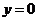
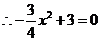
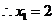 ,
,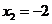
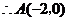 ,
,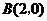 ··············································· 1分
··············································· 1分
又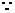 点
点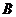 在
在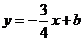 上
上
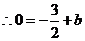
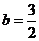
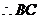 的解析式为
的解析式为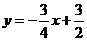 ·············································································· 2分
·············································································· 2分
(2)由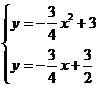 ,得
,得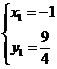
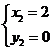 ···················································· 4分
···················································· 4分
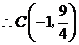 ,
,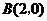
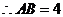 ,
,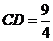 ······························································································· 5分
······························································································· 5分
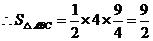 ························································································· 6分
························································································· 6分
(3)过点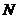 作
作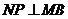 于点
于点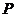
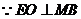
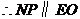
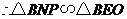 ······························································································· 7分
······························································································· 7分
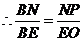 ·········································································································· 8分
·········································································································· 8分
由直线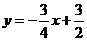 可得:
可得: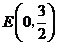
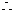 在
在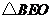 中,
中,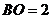 ,
,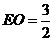 ,则
,则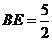
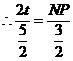 ,
,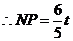 ······················································································· 9分
······················································································· 9分
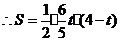
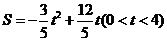 ···················································································· 10分
···················································································· 10分
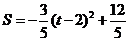 ····························································································· 11分
····························································································· 11分
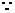 此抛物线开口向下,
此抛物线开口向下,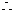 当
当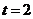 时,
时,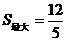
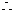 当点
当点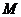 运动2秒时,
运动2秒时,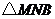 的面积达到最大,最大为
的面积达到最大,最大为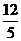 .···························· 12分
.···························· 12分
94.(08山东济宁26题)(12分)
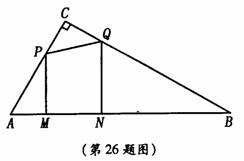
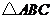 中,
中,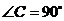 ,
,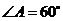 ,
,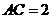 cm.长为1cm的线段
cm.长为1cm的线段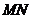 在
在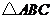 的边
的边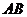 上沿
上沿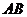 方向以1cm/s的速度向点
方向以1cm/s的速度向点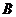 运动(运动前点
运动(运动前点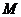 与点
与点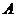 重合).过
重合).过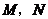 分别作
分别作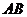 的垂线交直角边于
的垂线交直角边于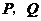 两点,线段
两点,线段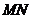 运动的时间为
运动的时间为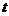 s.
s.
(1)若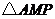 的面积为
的面积为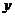 ,写出
,写出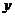 与
与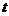 的函数关系式(写出自变量
的函数关系式(写出自变量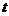 的取值范围);
的取值范围);
(2)线段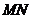 运动过程中,四边形
运动过程中,四边形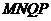 有可能成为矩形吗?若有可能,求出此时
有可能成为矩形吗?若有可能,求出此时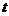 的值;若不可能,说明理由;
的值;若不可能,说明理由;
(3)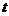 为何值时,以
为何值时,以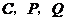 为顶点的三角形与
为顶点的三角形与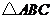 相似?
相似?
(08山东济宁26题解析)解:(1)当点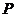 在
在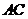 上时,
上时,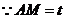 ,
,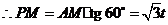 .
.
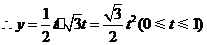 .········································································ 2分
.········································································ 2分
当点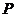 在
在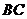 上时,
上时,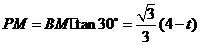 .
.
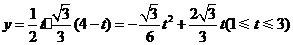 .·················································· 4分
.·················································· 4分
(2)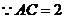 ,
,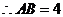 .
.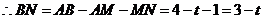 .
.
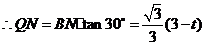 .········································································ 6分
.········································································ 6分
由条件知,若四边形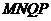 为矩形,需
为矩形,需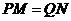 ,即
,即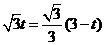 ,
,
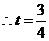 .
.
 当
当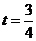 s时,四边形
s时,四边形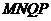 为矩形.································································· 8分
为矩形.································································· 8分
(3)由(2)知,当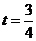 s时,四边形
s时,四边形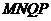 为矩形,此时
为矩形,此时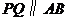 ,
,
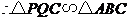 .··························································································· 9分
.··························································································· 9分
除此之外,当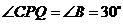 时,
时,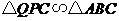 ,此时
,此时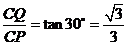 .
.
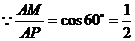 ,
,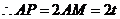 .
.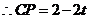 .····························· 10分
.····························· 10分
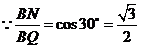 ,
,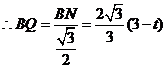 .
.
又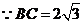 ,
,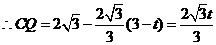 .········································ 11分
.········································ 11分
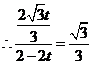 ,
,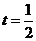 .
.
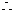 当
当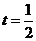 s或
s或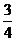 s时,以
s时,以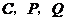 为顶点的三角形与
为顶点的三角形与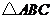 相似.··················· 12分
相似.··················· 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com