
8.直线l的方程为y=x+3,在l上任取一点P,若过点P且以双曲线12x2-4y2=3的焦点作椭圆的焦点,那么具有最短长轴的椭圆方程为_________.
7.(2006年兖州)设P为双曲线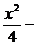 y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是 .
y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是 .
6.(2005年广州)已知点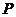 是抛物线
是抛物线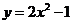 上的动点,定点
上的动点,定点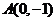 ,若点
,若点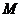 分
分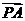 所成的比为2:1,则点
所成的比为2:1,则点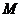 的轨迹方程是 。
的轨迹方程是 。
5.(2005年佛山)点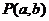 是单位圆的动点,则点
是单位圆的动点,则点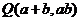 的轨迹方程是 。
的轨迹方程是 。
4.(2007江西)一动点到两坐标轴的距离之和的2倍等于动点到原点距离的平方,则动点 的轨迹方程为( )
的轨迹方程为( )
A.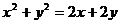 B.
B.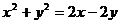
C.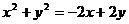 D.
D.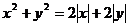
3.若θ∈[0,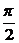 ],则椭圆x2+2y2-2
],则椭圆x2+2y2-2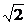 xcosθ+4ysinθ=0的中心的轨迹是( )
xcosθ+4ysinθ=0的中心的轨迹是( )
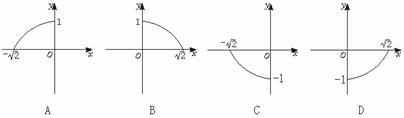
2.经过抛物线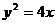 的焦点的弦的中点轨迹方程是
的焦点的弦的中点轨迹方程是
A.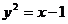 B.
B.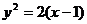 C.
C.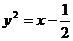 D.
D.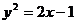
1.设k>1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
A.长轴在y轴上的椭圆 B.长轴在x轴上的椭圆
C.实轴在y轴上的双曲线 D.实轴在x轴上的双曲线
6.已知点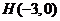 ,点
,点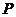 在
在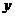 轴上,点
轴上,点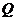 在
在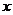 轴的正半轴上,点
轴的正半轴上,点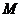 在直线
在直线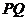 上,且满足
上,且满足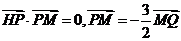 .
.
(1)当点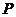 在
在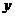 轴上移动时,求点
轴上移动时,求点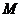 的轨迹
的轨迹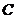 ;
;
(2)过点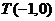 作直线
作直线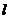 与轨迹
与轨迹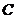 交于
交于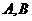 两点,若
两点,若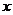 轴上存在一点
轴上存在一点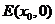 ,使得
,使得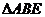 是等边三角形,求
是等边三角形,求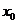 的值。
的值。
[能力提升]
5.已知椭圆C的方程为x2+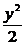 =1,点P(a,b)的坐标满足a2+
=1,点P(a,b)的坐标满足a2+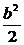 ≤1,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
≤1,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
(1)点Q的轨迹方程;
(2)点Q的轨迹与坐标轴的交点的个数.
例6.已知常数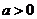 ,向量
,向量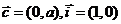 ,经过原点
,经过原点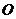 以
以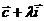 为方向向量的直线与经过定点
为方向向量的直线与经过定点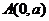 ,以
,以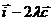 为方向向量的直线相交于点
为方向向量的直线相交于点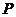 ,其中
,其中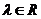 .试问:是否存在两个定点
.试问:是否存在两个定点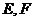 ,使得
,使得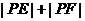 为定值,若存在,求出点
为定值,若存在,求出点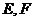 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
[剖析]由于向量可以用一条有向线段来表示,有向线段的方向可以决定解析几何中直线的斜率,故直线的方向向量与解析几何中的直线有着天然的联系。求解此类问题的关键是:根据直线的方向向量得出直线方程,再转化为解析几何问题解决。从求点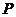 的轨迹方程入手,进而讨论轨迹方程的性质,便可获得本题的解答.
的轨迹方程入手,进而讨论轨迹方程的性质,便可获得本题的解答.
[解]因为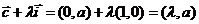 ,
,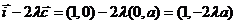
所以直线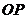 与
与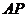 的方程分别为:
的方程分别为: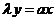 和
和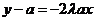 ,其中
,其中 .
.
消去实数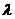 ,得点
,得点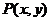 的坐标满足方程
的坐标满足方程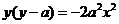 ,
,
整理得: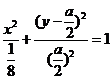 ①
①
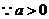 ,所以
,所以
(1)当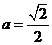 时,方程①是圆的方程,故不存在合乎题意的定点
时,方程①是圆的方程,故不存在合乎题意的定点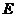 和
和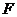 ;
;
(2)当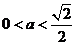 时,方程①表示椭圆,故焦点坐标
时,方程①表示椭圆,故焦点坐标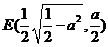 和
和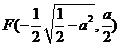 为合乎题意的两个定点;
为合乎题意的两个定点;
(3)当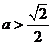 时,方程①也表示椭圆,故焦点
时,方程①也表示椭圆,故焦点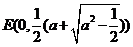 和
和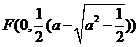 为符合题意的两个定点.
为符合题意的两个定点.
[警示]本题以向量为载体考直线,消元法求轨迹,以圆与椭圆的有关知识,考查了分类讨论思想。以向量为载体考查圆锥曲线问题是最近几何高考的热点问题,要正确认识向量等式所表示的几何意义,将向量运算的数量化是解决本类问题的关键.
[变式训练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com