
1.过点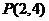 作直线与抛物线
作直线与抛物线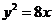 只有一个公共点,这样的直线有( )
只有一个公共点,这样的直线有( )
(A)1条 (B)2 条 (C)3条 (D)4条
4.与焦点弦有关的问题,要注意应用圆锥曲线的定义,涉及到中点的问题,除利用韦达定理以外,用“点差法”也较为简单。
[基础闯关]
3.在判断直线与圆锥曲线的位置关系时,要注意数形结合,以形辅数的方法;
2.解决直线与圆锥曲线相交问题时,不要忽视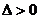 这一条件;
这一条件;
1.解决直线与圆锥曲线的交点问题时,常会出现漏解的情况,用代数法求解时,易忽视消元后一元二次方程的二项式系数是否为零的讨论;在利用几何法解题时,易忽视特殊情况的讨论,如与双曲线的渐近线平行,与抛物线的对称轴平行等特殊情况;这些情况要特别加以注意;
4.(1)斜率为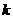 的直线与圆锥曲线相交于两点
的直线与圆锥曲线相交于两点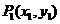 ,
, ,则所得的弦长
,则所得的弦长
或
,其中求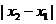 与
与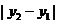 时,常使用韦达定理,即做如下变形:
时,常使用韦达定理,即做如下变形: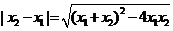 ,
,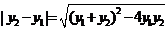 .
.
(2)当直线的斜率不存在时,可求出交点的坐标,直接运算;
(3)经过圆锥曲线的焦点的弦(也称为焦点弦)的长度问题,可利用圆锥曲线的定义,将其转化为 ,往往比利用弦长公式简单。
[特别提醒]
直线与圆锥曲线的位置关系一直为高考的热点,这类问题常涉及到圆锥曲线的性质与直线的基本知识中的点、线段的中点、弦长、垂直问题,因此分析问题时要借助于数形结合思想、设而不求法及弦长公式及韦达定理综合考虑,这样就加强了对数学各种能力的考查。因此要注意对数学思想、数学方法的归纳与提炼,达到优化解题的目的。
已知弦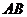 的中点,研究
的中点,研究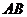 的斜率与方程.
的斜率与方程.
3. 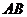 是椭圆
是椭圆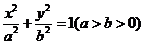 的一条弦,中点M坐标为
的一条弦,中点M坐标为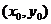 ,则直线的斜率为
。运用点差法求
,则直线的斜率为
。运用点差法求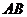 的斜率:设
的斜率:设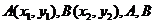 都在椭圆上,则
都在椭圆上,则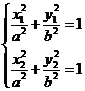 ,两式相减,得
,两式相减,得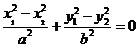 ,
,
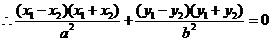 ,从而
,从而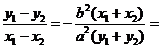 ,
,
故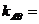 。
。
运用类比思想,可以推出已知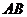 是双曲线
是双曲线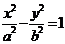 的弦,中点M
的弦,中点M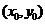 ,则
,则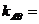 ;
;
已知抛物线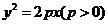 的弦
的弦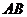 的中点M
的中点M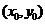 ,则
,则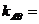 .
.
2.几何法:直线与圆锥曲线的位置关系可分为三类:
(1)直线与圆锥曲线没有公共点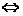 直线与圆锥曲线
;
直线与圆锥曲线
;
(2) 直线与圆锥曲线有且只有一个公共点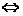 对椭圆而言,直线与椭圆 ;对双曲线而言,表示直线与其相切或与双曲线的渐近线 ,对于抛物线而言,表示直线与其 或与其对称轴平行;
对椭圆而言,直线与椭圆 ;对双曲线而言,表示直线与其相切或与双曲线的渐近线 ,对于抛物线而言,表示直线与其 或与其对称轴平行;
(3) 直线与圆锥曲线有个相异的公共点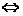 直线与圆锥曲线
,此时直线被圆锥曲线所截得的线段称为圆锥曲线的弦。
直线与圆锥曲线
,此时直线被圆锥曲线所截得的线段称为圆锥曲线的弦。
1.代数法:判断直线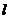 与圆锥曲线
与圆锥曲线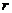 的位置关系时,通常将直线
的位置关系时,通常将直线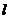 的方程
的方程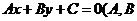 不同时为
不同时为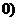 代入圆锥曲线
代入圆锥曲线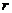 的方程
的方程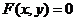 ,消去
,消去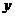 (也可以消去
(也可以消去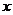 )得到一个关于变量
)得到一个关于变量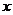 (或
(或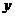 )的一元方程,即
)的一元方程,即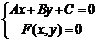 消去
消去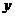 后得
后得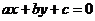 ,
,
(1)当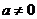 时,则有
时,则有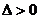 ,直线
,直线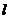 与曲线
与曲线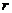 ;
;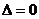 ,直线
,直线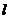 与曲线
与曲线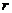 ;
;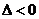 ,直线
,直线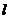 与曲线
与曲线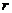 。
。
(2)当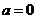 时,即得到一个一次方程,则
时,即得到一个一次方程,则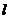 与
与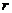 相交,且只有一个交点,此时,若
相交,且只有一个交点,此时,若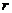 为双曲线,则直线
为双曲线,则直线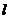 与双曲线的渐近线的位置关系是
;若
与双曲线的渐近线的位置关系是
;若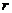 是抛物线,则直线
是抛物线,则直线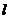 与抛物线的对称轴的位置关系是
。
与抛物线的对称轴的位置关系是
。
8.如图,倾角θ为30°的绝缘正方形斜面abcd,边长为2m,有一质量为m=0.01kg,带电量q=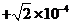 C的小滑块,与斜面间的动摩擦因数μ=
C的小滑块,与斜面间的动摩擦因数μ=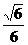 ,整个装置处在垂直于斜面向上的匀强磁场中,磁场的磁感应强度为0.4T,滑块在a点具有沿ac方向、大小v=30m/s的初速度,g取10m/s2。要使滑块由a点沿直线运动到达c点,应在绝缘斜面内加一个怎样的匀强电场?
,整个装置处在垂直于斜面向上的匀强磁场中,磁场的磁感应强度为0.4T,滑块在a点具有沿ac方向、大小v=30m/s的初速度,g取10m/s2。要使滑块由a点沿直线运动到达c点,应在绝缘斜面内加一个怎样的匀强电场?
 答案:⑴要使滑块沿直线到达c点,滑块必须作匀速直线运动,滑块在斜面所在平面内受力如图
答案:⑴要使滑块沿直线到达c点,滑块必须作匀速直线运动,滑块在斜面所在平面内受力如图
滑块重力沿斜面向下的分力为 Gx=mgsinθ=0.05N
Gx在速度方向的分力为 Gx1=mgsinθcos450=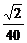 N
N
滑块受到的滑动摩擦力为 f=μmgcosθ=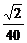 N= Gx1
N= Gx1
由于滑块受力平衡,设所加电场的场强为E,则;电场力 F电=F洛+ Gxsin 450
即 qE=qvB+ Gxsin 450 解得: E=262 N/C 方向:与ab方向成450沿斜面斜向上方
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com