
4.欧拉示性数:
在欧拉公式中令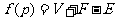 ,
,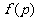 叫欧拉示性数
叫欧拉示性数
说明:(1)简单多面体的欧拉示性数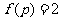 .
.
(2)带一个洞的多面体的欧拉示性数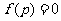 .例如:长方体挖去一个洞连结底面相应顶点得到的多面体
.例如:长方体挖去一个洞连结底面相应顶点得到的多面体 .
.
4.欧拉定理(欧拉公式):简单多面体的顶点数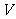 、面数
、面数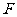 及棱数
及棱数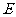 有关系式:
有关系式:
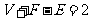 .
.
证明:(方法一)
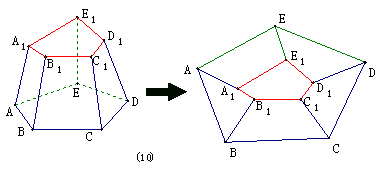
⑴如图⑽:将多面体的底面ABCDE剪掉,抻成平面图形,其顶点、棱数,面数(剪掉面用右图中ABCDE表示)均没有变,故所有面的内角总和不变。
⑵设左图中共有F个面,分别是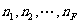 边形,顶点数为V,棱数为E,则
边形,顶点数为V,棱数为E,则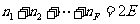 .
.
左图中,所有面的内角总和为
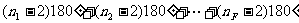
=
=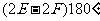
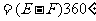
⑶右图中,所有面的内角总和为
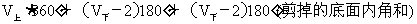
=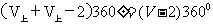
⑷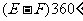 =
=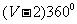
整理得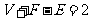 .
.
(方法二)以四面体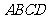 为例来说明:
为例来说明:
将它的一个面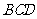 去掉,并使其变为平面图形,四面体的顶点数
去掉,并使其变为平面图形,四面体的顶点数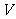 、棱数
、棱数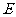 与剩下的面数
与剩下的面数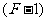 变形后都没有变
变形后都没有变 因此,要研究
因此,要研究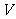 、
、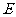 和
和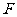 的关系,只要去掉一个面,将它变形为平面图形即可
的关系,只要去掉一个面,将它变形为平面图形即可
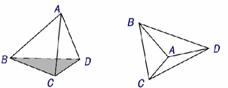
对平面图形,我们来研究:
(1)去掉一条棱,就减少一个面 例如去掉
例如去掉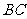 ,就减少一个面
,就减少一个面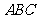 .
.
同理,去掉棱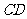 、
、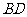 ,也就各减少一个面
,也就各减少一个面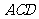 、
、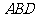 .
.
所以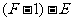 、
、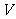 的值都不变,因此
的值都不变,因此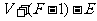 的值也不变
的值也不变
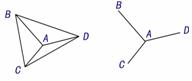
(2)再从剩下的树枝形中,去掉一条棱,就减少一个顶点 例如去掉
例如去掉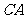 ,就减少一个顶点
,就减少一个顶点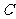 .同理,去掉
.同理,去掉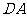 就减少一个顶点
就减少一个顶点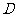 ,最后剩下
,最后剩下
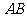 (如图).
(如图).
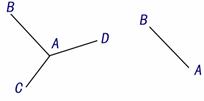
在此过程中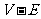 的值不变,但这时面数
的值不变,但这时面数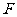 是
是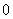 ,
,
所以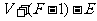 的值也不变
的值也不变
由于最后只剩下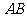 ,所以
,所以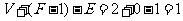 ,
,
最后加上去掉的一个面,就得到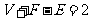 .
.
3. 假如图⑸→图⑻的多面体表面是像皮膜,向内充气则⑸⑹将变成一个球面,图⑺将变成两个紧贴的球面,图⑻将变成一个环面。

可以验证:只有像⑸⑹这样,经过连续变形,表面能变为一个球面的多面体才满足公式V+F-E=2。这个公式称为欧拉公式,这样的多面体称为简单多面体。
2.查出图⑺中的顶点数V、面数F、和棱数E,并验证上面公式是否还成立?

1.请查出图⑹的顶点数V、面数F、和棱数E,并计算V+F-E=6+6-10=2
3.欧拉公式的探究
2.五种正多面体的顶点数、面数及棱数:
|
正多面体 |
顶点数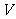 |
面数 |
棱数 |
|
正四面体 |
4 |
4 |
6 |
|
正六面体 |
8 |
6 |
12 |
|
正八面体 |
6 |
8 |
12 |
|
正十二面体 |
20 |
12 |
30 |
|
正二十面体 |
12 |
20 |
30 |
 发现:它们的顶点数
发现:它们的顶点数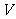 、面数
、面数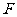 及棱数
及棱数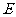 有共同的关系式:
有共同的关系式: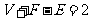 .
.
上述关系式对简单多面体都成立
1.简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面 如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体
如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体
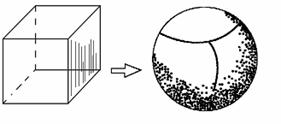
说明:棱柱、棱锥、正多面体等一切凸多面体都是简单多面体
4.凸多面体的分类:多面体至少有四个面,按照它的面数分别叫四面体、五面体、六面体等
1  欧拉生平事迹简说:欧拉(Euler),瑞士数学家及自然科学家
欧拉生平事迹简说:欧拉(Euler),瑞士数学家及自然科学家 1707年4月15日出生于瑞士巴塞尔的一个牧师家庭,自幼受父亲的教育,13岁入读巴塞尔大学15岁大学毕业,16岁获硕士学位,1783年9月18日于俄国彼得堡去逝
1707年4月15日出生于瑞士巴塞尔的一个牧师家庭,自幼受父亲的教育,13岁入读巴塞尔大学15岁大学毕业,16岁获硕士学位,1783年9月18日于俄国彼得堡去逝 (详细资料附后)
(详细资料附后)
2 多面体的概念:由若干个多边形围成的空间图形叫多面体;每个多边形叫多面体的面,两个面的公共边叫多面体的棱,棱和棱的公共点叫多面体的顶点,连结不在同一面上的两个顶点的线段叫多面体的对角线.
多面体的概念:由若干个多边形围成的空间图形叫多面体;每个多边形叫多面体的面,两个面的公共边叫多面体的棱,棱和棱的公共点叫多面体的顶点,连结不在同一面上的两个顶点的线段叫多面体的对角线.
3.凸多面体:把多面体的任一个面展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫凸多面体.如图的多面体则不是凸多面体.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com