27．标准正态曲线:当μ=0、σ=l时，正态总体称为标准正态总体，其相应的函数表示式是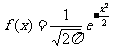，(-∞＜x＜+∞)

其相应的曲线称为标准正态曲线

标准正态总体N(0，1)在正态总体的研究中占有重要的地位 任何正态分布的概率问题均可转化成标准正态分布的概率问题

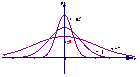
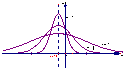
26．正态曲线的性质：

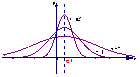
(1)曲线在x轴的上方，与x轴不相交

(2)曲线关于直线x=μ对称

(3)当x=μ时，曲线位于最高点

(4)当x＜μ时，曲线上升(增函数)；当x＞μ时，曲线下降(减函数) 并且当曲线向左、右两边无限延伸时，以x轴为渐近线，向它无限靠近

(5)μ一定时，曲线的形状由σ确定

σ越大，曲线越“矮胖”，总体分布越分散；

σ越小．曲线越“高”．总体分布越集中：

五条性质中前三条学生较易掌握，后两条较难理解，因此在讲授时应运用数形结合的原则，采用对比教学

25．正态分布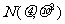)是由均值μ和标准差σ唯一决定的分布

24．正态分布密度函数：

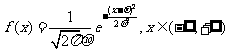，(σ＞0)

其中π是圆周率；e是自然对数的底；x是随机变量的取值；μ为正态分布的均值；σ是正态分布的标准差.正态分布一般记为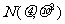

23.总体密度曲线:样本容量越大，所分组数越多，各组的频率就越接近于总体在相应各组取值的概率．设想样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线．

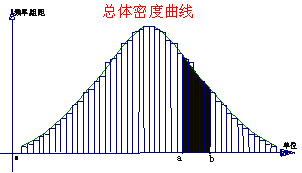
它反映了总体在各个范围内取值的概率．根据这条曲线，可求出总体在区间(a，b)内取值的概率等于总体密度曲线，直线x=a，x=b及x轴所围图形的面积．

22.不放回抽样和放回抽样:在抽样中，如果每次抽出个体后不再将它放回总体，称这样的抽样为不放回抽样；如果每次抽出个体后再将它放回总体，称这样的抽样为放回抽样．

随机抽样、系统抽样、分层抽样都是不放回抽样

21.分层抽样: 当已知总体由差异明显的几部分组成时，为了使样本更充分地反映总体的情况，常将总体分成几部分，然后按照各部分所占的比例进行抽样，这种抽样叫做分层抽样，所分成的部分叫做层

　 常用的抽样方法及它们之间的联系和区别：

20.系统抽样:当总体中的个体数较多时，可将总体分成均衡的几个部分，然后按预先定出的规则，从每一部分抽取一个个体，得到需要的样本，这种抽样叫做系统抽样．系统抽样的步骤：①采用随机的方式将总体中的个体编号为简便起见，有时可直接采用个体所带有的号码，如考生的准考证号、街道上各户的门牌号，等等 ②为将整个的编号分段(即分成几个部分)，要确定分段的间隔k当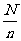(N为总体中的个体的个数，n为样本容量)是整数时，k=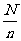;当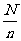不是整数时，通过从总体中剔除一些个体使剩下的总体中个体的个数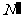能被n整除，这时k=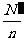.③在第一段用简单随机抽样确定起始的个体编号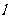 ④按照事先确定的规则抽取样本(通常是将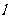加上间隔k，得到第2个编号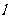+k,第3个编号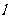+2k，这样继续下去，直到获取整个样本)

①系统抽样适用于总体中的个体数较多的情况，它与简单随机抽样的联系在于：将总体均分后的每一部分进行抽样时，采用的是简单随机抽样；

②与简单随机抽样一样，系统抽样是等概率抽样，它是客观的、公平的．

③总体中的个体数恰好能被样本容量整除时，可用它们的比值作为系统抽样的间隔；当总体中的个体数不能被样本容量整除时，可用简单随机抽样先从总体中剔除少量个体，使剩下的个体数能被样本容量整除在进行系统抽样

19.随机数表法： 随机数表抽样“三步曲”：第一步，将总体中的个体编号；第二步，选定开始的数字；第三步，获取样本号码

18.抽签法：先将总体中的所有个体(共有N个)编号(号码可从1到N)，并把号码写在形状、大小相同的号签上(号签可用小球、卡片、纸条等制作)，然后将这些号签放在同一个箱子里，进行均匀搅拌，抽签时每次从中抽一个号签，连续抽取n次，就得到一个容量为n的样本

适用范围：总体的个体数不多时

优点：抽签法简便易行，当总体的个体数不太多时适宜采用抽签法．