
2.等比数列中的重要性质:
(1)若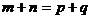 ,则
,则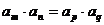 ;
;
(2)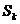 ,
,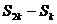 ,
, 成等比数列;
成等比数列;
(3)若{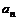 }是等差数列,则{
}是等差数列,则{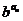 }是等比数列,若{
}是等比数列,若{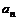 }是等比数列且
}是等比数列且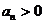 ,则{
,则{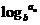 }是等差数列;
}是等差数列;
(4)类比等差数列而得的有关结论
练习:
①若{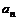 }是等比数列,
}是等比数列,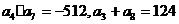 ,公比
,公比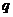 为整数,则
为整数,则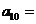
②已知数列{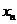 }满足
}满足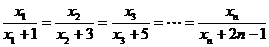 ,并且
,并且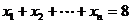 ,那么
,那么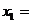
③等差数列{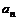 }满足
}满足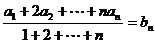 ,则{
,则{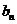 }也是等差数列,类比等比数列{
}也是等差数列,类比等比数列{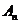 }满足
}满足
1.等差数列中的重要性质:
(1)若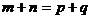 ,则
,则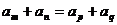 ;
;
(2)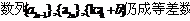 ;
;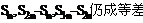 数列;
数列;
 (3)若{
(3)若{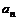 },{
},{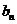 }是等差数列,
}是等差数列,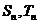 分别为它们的前
分别为它们的前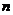 项和,则
项和,则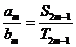 ;
;
(4)在等差数列中,求Sn 的最大(小)值,其中一个思路是找出最后一正项(负项) ,那么
,那么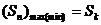
练习:
①在等差数列{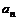 }中,若
}中,若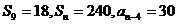 ,则
,则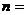
②{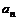 },{
},{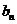 }都是等差数列,前
}都是等差数列,前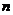 项和分别为
项和分别为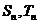 ,且
,且 ,则
,则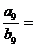
③若{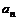 }的首项为14,前
}的首项为14,前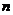 和为
和为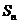 ,点
,点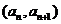 在直线
在直线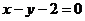 上,那
上,那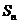 最大时,
最大时,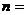
13.在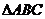 中,判断下列命题的正误
中,判断下列命题的正误
(1)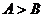 的充要条件是
的充要条件是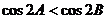
(2) 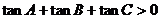 ,则
,则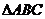 是锐角三角形
是锐角三角形
(3)若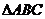 是锐角三角形,则
是锐角三角形,则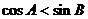
12.有关斜三角形的几个结论:
 在
在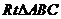 中,
中,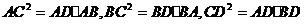
内切圆半径
 (S为
(S为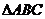 的面积)
的面积)
在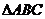 中,
中,
①
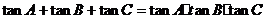
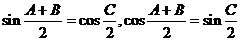
②正弦定理
③余弦定理
④面积公式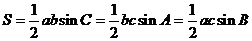
⑤内切圆半径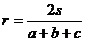
11.三角函数图像变换:
(1)将函数为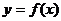 的图像向右平移
的图像向右平移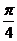 个单位后,再作关于
个单位后,再作关于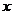 轴的对称变换,得到函数
轴的对称变换,得到函数 的图像,则
的图像,则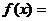
(2)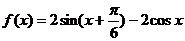 的图像按向量
的图像按向量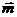 平移得到
平移得到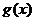 的图像,若
的图像,若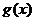 是偶函数,求
是偶函数,求 最小的向量
最小的向量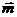
10. 三角函数(正弦、余弦、正切)图象的草图能迅速画出吗?能写出他们的单调区、对称轴,取最值时的x值的集合吗?(别忘了k Z)
Z)
三角函数性质要记牢.函数y=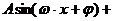 k的图象及性质:
k的图象及性质:
振幅|A|,周期T=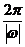 , 若x=x0为此函数的对称轴,则x0是使y取到最值的点,反之亦然,使y取到最值的x的集合为
, 当
, 若x=x0为此函数的对称轴,则x0是使y取到最值的点,反之亦然,使y取到最值的x的集合为
, 当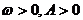 时函数的增区间为
,减区间为
;当
时函数的增区间为
,减区间为
;当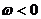 时要利用诱导公式将
时要利用诱导公式将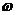 变为大于零后再用上面的结论.
变为大于零后再用上面的结论.
五点作图法:令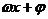 依次为
依次为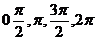 求出x与y,依点
求出x与y,依点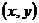 作图
作图
练习:
如图,摩天轮的半径为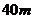 ,点
,点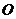 距地面的高度为
距地面的高度为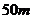 ,摩天轮做匀速转动,每
,摩天轮做匀速转动,每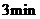 转一圈,摩天轮上的点
转一圈,摩天轮上的点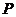 的起始位置在最低点处,(1)试确定在时刻
的起始位置在最低点处,(1)试确定在时刻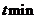 时点
时点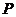 距地面的高度;(2)摩天轮转动的一圈内,有多长时间点
距地面的高度;(2)摩天轮转动的一圈内,有多长时间点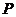 距地面超过
距地面超过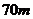 ?
?


9.
辅助角公式: (其中
(其中 角所在的象限由a, b 的符号确定,
角所在的象限由a, b 的符号确定, 角的值由
角的值由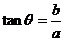 确定)在求最值、化简时起着重要作用.
确定)在求最值、化简时起着重要作用.
8.
你还记得在弧度制下弧长公式和扇形面积公式吗?(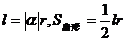 )
)
7. 你还记得某些特殊角的三角函数值吗?会求吗?
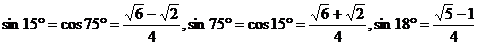
练习:
 (1)
(1)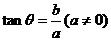 是
是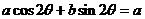 的
条件.
的
条件.
解析:
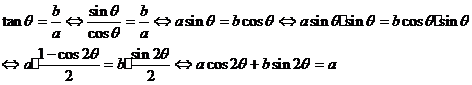
反之,若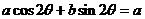 成立,则未必有
成立,则未必有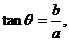 取
取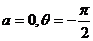 即可,故为充分不必要条件
即可,故为充分不必要条件
易错原因:未考虑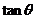 不存在的情况
不存在的情况
(2)已知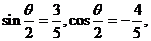 则
则 角的终边在
角的终边在
解析:因为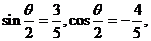 故
故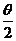 是第二象限角,即
是第二象限角,即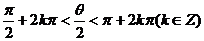 ,故
,故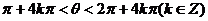 ,在第三或第四象限
,在第三或第四象限
以上的结果是错误的,正确的如下:
由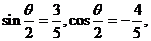 知
知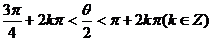
所以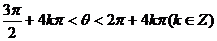 ,故在第四象限
,故在第四象限
易错原因:角度的存在区间范围过大
6. 你还记得三角化简的通性通法吗?(切化弦、降幂公式、用三角公式转化出现特殊角. 异角化同角,异名化同名,高次化低次);你还记得降幂公式吗?cos2x=(1+cos2x)/2;sin2x=(1-cos2x)/2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com