
8.提示: 设切去的正方形边长为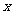 ,无盖方底盒子的容积为
,无盖方底盒子的容积为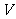 ,则
,则

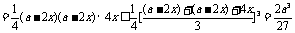
当且仅当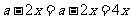 ,即当
,即当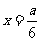 时,不等式取等号,此时
时,不等式取等号,此时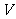 取最大值
取最大值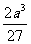 .即当切去的小正方形边长是原来正方形边长的
.即当切去的小正方形边长是原来正方形边长的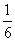 时,盒子容积最大.
时,盒子容积最大.
7.提示:  ;
;
6.提示: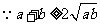 ,
, ,
,
分别将以上三式相乘或相加即可;
5. 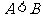 .
.
提示:通过考察它们的差与0的大小关系,得出这两个多项式的大小关系.
因为
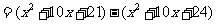

所以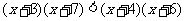 ;
;
4.C. 提示: ;
;
3.D.提示:当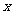 ≤-2时,原不等式可以化为
≤-2时,原不等式可以化为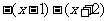 ≥5,
≥5,
解得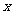 ≤-3,即不等式组
≤-3,即不等式组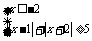 的解集是
的解集是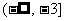 .
.
当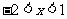 时,原不等式可以化为
时,原不等式可以化为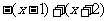 ≥5,
≥5,
即3≥5,矛盾.所以不等式组 ,的解集为
,的解集为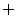 ,
,
当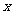 ≥1时,原不等式可以化为
≥1时,原不等式可以化为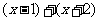 ≥5,解得
≥5,解得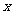 ≥2,
≥2,
即不等式组 的解集是
的解集是 .
.
综上所述,原不等式的解集是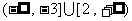 ;
;
2.B.提示:先移项,再通分,再化简;
1.D.提示:注意函数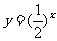 的单调性;
的单调性;
18. 设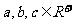 ,求证:
,求证: .
.
不 等 式 选 讲 答 案
17.证明: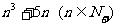 能够被6整除.
能够被6整除.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com