练习册

  • 练习册
  • 试题
     0  47297  47305  47311  47315  47321  47323  47327  47333  47335  47341  47347  47351  47353  47357  47363  47365  47371  47375  47377  47381  47383  47387  47389  47391  47392  47393  47395  47396  47397  47399  47401  47405  47407  47411  47413  47417  47423  47425  47431  47435  47437  47441  47447  47453  47455  47461  47465  47467  47473  47477  47483  47491  447090 

    ∵CE=，AC=1 , ∴CD=

    试题详情

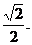
    ∠ACB=900，AC=1，C点到AB1的距离为CE=，D为AB的中点.

    （1）求证：AB­1⊥平面CED；

    （2）求异面直线AB1与CD之间的距离；

    【解】（1）∵D是AB中点，△ABC为等腰直角三角形，∠ABC=900，∴CD⊥AB又AA1⊥平面ABC，∴CD⊥AA1.

    ∴CD⊥平面A1B1BA  ∴CD⊥AB1，又CE⊥AB1， ∴AB1⊥平面CDE；

    （2）由CD⊥平面A1B1BA  ∴CD⊥DE

    ∵AB1⊥平面CDE  ∴DE⊥AB1

    ∴DE是异面直线AB1与CD的公垂线段

    试题详情

    5．【江苏?启东中学模拟】

    试题详情

    而E A1面AD C1内，故A1E∥平面AD C1． …………………………14分

     

    试题详情

    当，即E为B1C1的中点时，A1E∥平面ADC1．…………………8分

    事实上，正三棱柱ABC－A1B1C1中，四边形BC C1 B1是矩形，且D、E分别是BC、B1C1的中点，所以B1B∥DE，B1B= DE． ……………………10分

    又B1B∥AA1，且B1B=AA1，

    ∴DE∥AA1，且DE=AA1．  …………………………………………12分

    所以四边形ADE A1为平行四边形，所以E A1∥AD．

    试题详情

    解: （1）在正三棱柱中，C C1⊥平面ABC，AD平面ABC，

    ∴ AD⊥C C1．………………………2分

    又AD⊥C1D，C C1交C1D于C1，且C C1和C1D都在面BC C1 B1内，

                  ∴ AD⊥面BC C1 B1．   ……………………………………………5分

    （2）由（1），得AD⊥BC．在正三角形ABC中，D是BC的中点．…………7分

    试题详情

    （2）设E是B1C1上的一点，当的值为多少时，

    A1E∥平面ADC1？请给出证明．

     

    试题详情

    （1）求证：AD⊥平面BC C1 B1；

    试题详情

    4．【江苏?南通】15．（本小题14分）

    如图，在正三棱柱ABC－A1B1C1中，点D在边BC上，AD⊥C1D．

    试题详情

    所以直线与平面所成角的正弦值为.………………………………10分

     

    试题详情


    同步练习册答案