【例6】设P是双曲线右支上任一点.

当且仅当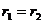时，cosθ=0，∴θ。

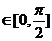（2）设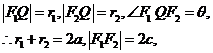

∵是共线向量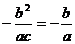，∴，∴b=c,故。

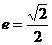解：（1）∵，∴。

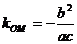【例5】已知椭圆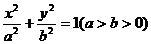的长、短轴端点分别为A、B，从此椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点F₁，向量与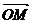是共线向量。

（1）求椭圆的离心率e；

（2）设Q是椭圆上任意一点， F₁、F₂分别是左、右焦点，求∠F₁QF₂的取值范围；

X_B=|BF|=|BN|=6．   

设点P (x，y)是曲线段C上任一点，则由题意知P属于集合

{(x，y)|(x－x_N)²+y²=x²，x_A≤x≤x_B，y＞0}．    

故曲线段C的方程

y²=8(x－2)(3≤x≤6，y＞0)．     

第十七讲  圆锥曲线的定义、性质和方程(二)

=|ME|+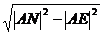=4

x_N=|AE|+|EN|=4．