
科目: 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
我们知道,无限循环小数都可以转化为分数.例如:将0. 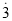 转化为分数时,可设0.
转化为分数时,可设0. 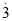 =
= 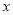 ,则
,则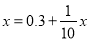 ,解得
,解得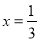 ,即0.
,即0. 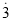 =
=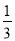 .仿此方法,将0.
.仿此方法,将0. 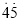 化成分数是_______.
化成分数是_______.
查看答案和解析>>
科目: 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
一个商店把某件商品按进价提高20%作为定价,可是总卖不出去;后来按定价减价20%出售,很快卖掉,结果这次生意亏了4元.那么这件商品的进价是________元.
100 【解析】根据题意可得关于x的方程,求解可得商品的进价. 【解析】 根据题意:设未知进价为x, 可得:x•(1+20%)•(1-20%)=96 解得:x=100;查看答案和解析>>
科目: 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
某市为提倡节约用水,采取分段收费.若每户每月用水量不超过20 m3,每立方米收费2元;若用水量超过20 m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水________.
28 m3 【解析】试题分析:64>40可以判定小明家用水超过20,可以设用水位x,则40+3(x-20)=64,解得x=28,查看答案和解析>>
科目: 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
瑞士中学教师巴尔末成功的从光谱数据:  ,
,  ,
,  ,
, 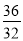 ,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.
,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
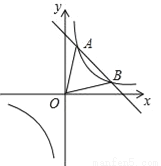
如图,一次函数y=kx+b与反比例函数y= 的图象交于A(1,6),B(3,n)两点.
的图象交于A(1,6),B(3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象写出不等式kx+b﹣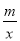 >0的解集;
>0的解集;
(3)若点M在x轴上、点N在y轴上,且以M、N、A、B为顶点的四边形是平行四边形,请直接写出点M、N的坐标.
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
小明想知道湖中两个小亭A、B之间的距离,他在与小亭A、B位于同一水平面且东西走向的湖边小道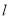 上某一观测点M处,测得亭A在点M的北偏东30°方向, 亭B在点M的北偏东60°方向,当小明由点M沿小道
上某一观测点M处,测得亭A在点M的北偏东30°方向, 亭B在点M的北偏东60°方向,当小明由点M沿小道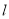 向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.
向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题:
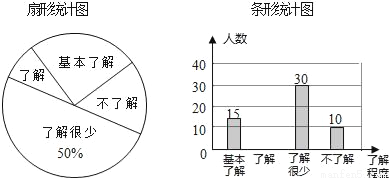
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;
(2)请补全条形统计图;
(3)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
(1)60;90°;(2)补图见解析;(3) 【解析】试题分析:(1)根据了解很少的人数和所占的百分百求出抽查的总人数,再用“基本了解”所占的百分比乘以360°,即可求出“基本了解”部分所对应扇形的圆心角 的度数; (2)用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数,求出了解的人数,从而补全统计图; (3)根据题意先画出树状图,再根据概率公式即可得出答案....查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
设a是方程x2﹣2006x+1=0的一个根,求代数式a2﹣2007a+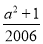 的值.
的值.
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
设a是方程x2﹣2006x+1=0的一个根,求代数式a2﹣2007a+ 的值.
的值.
【答案】-1
【解析】【试题分析】根据方程的根的定义,则x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,得a2﹣2007a+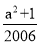 =
= .
.
【试题解析】
把x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,
所以a2-2007a=-a-1,
所以a2-2007a+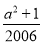 =-a-1+
=-a-1+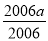 =-1,即a2-2007a+
=-1,即a2-2007a+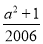 =-1.
=-1.
【方法点睛】本题目是一道考查一元二次方程的根的定义,方程的根满足该方程,代入得到相关代数式的值,进而将所求的额代数式进行转化,化简,求值.题目难度一般.
【题型】解答题
【结束】
5
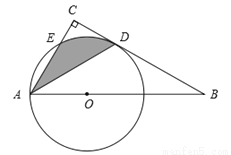
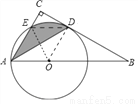
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
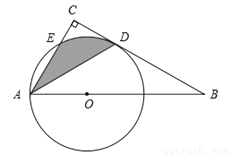
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
【答案】(1)∠CAD的度数为30°;
(2)阴影部分的面积为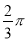 .
.
【解析】试题分析:(1)连接OD.由切线的性质可知OD⊥BC,从而可证明AC∥OD,由平行线的性质和等腰三角形的性质可证明∠CAD=∠OAD;(2)连接OE,ED、OD.先证明ED∥AO,然后依据同底等高的两个三角形的面积相等可知S△AED=S△EDO,于是将阴影部分的面积可转化为扇形EOD的面积求解即可.
试题解析:(1)连接OD,
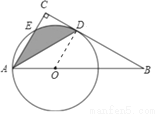
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
又∵AC⊥BC,
∴OD∥AC,
∴∠ADO=∠CAD.
又∵OD=OA,
∴∠ADO=∠OAD,
∴∠CAD=∠OAD=30°.
(2)连接OE,ED.
∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵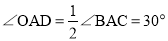 ,
,
∴∠ADE=∠OAD,
∴ED∥AO,
∴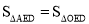
∴阴影部分的面积 = 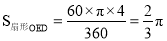 .
.
【题型】解答题
【结束】
6
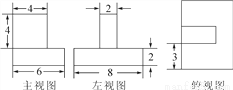
如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com