
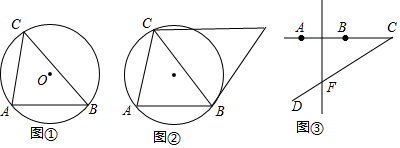
���� ��1�����Ż�AB������ȡһ��D������AD��BD�����ADB=��ACB������ͬ�����Ե�Բ�ܽ���ȼ���֤����
��2����ͼ���У�����C��ֱ��l���O���ڵ�E����CE���ӳ�����ȡһ��P������PA��PB�����APB����ACB����AP����O��F���ɡ�AFB����APB����AFB=��ACB������֤����
��3����ͼ���У���������A��B�Һ�ֱ��CD���е�Բ���е�ΪP����ʱ��APB��������߳��������ɼ��㣮
��� �⣺��1����ͼ���У�
���Ż�AB������ȡһ��D������AD��BD�����ADB=��ACB��
���ɣ���$\widehat{AB}$=$\widehat{AB}$��
���ADB=��ACB��
��2����ͼ���У�����C��ֱ��l���O���ڵ�E����CE���ӳ�����ȡһ��P������PA��PB�����APB����ACB��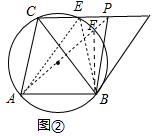
���ɣ���AP����O��F��
�ߡ�AFB����APB����AFB=��ACB��
���APB����ACB��
��3����ͼ���У���������A��B�Һ�ֱ��CD���е�Բ���е�ΪP����ʱ��APB���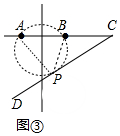
��PC�����ߣ�
��PC2=CB•CA��������֤����CPB�ס�CAP���õ�$\frac{CP}{CA}$=$\frac{CB}{CP}$��
��CB=5$\sqrt{2}$��AC=10$\sqrt{2}$��
��PC2=5$\sqrt{2}$��10$\sqrt{2}$=100��
��PC=10�ף�
�𣺵�P���C�ľ���Ϊ10�ף�
���� ���⿼��Բ�ۺ��⡢ͬ�����Ե�Բ�ܽ���ȡ����߳������������ε���Ǵ����κ�һ�������ڵ��ڽǵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ������п��������ͣ�


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���������߶�AB=2��CD=4����A�������ϱ�ʾ������-10����C�������ϱ�ʾ������16�����߶�AB��6����λ/����ٶ����������˶���ͬʱ�߶�CD��2����λ/����ٶ����������˶���
��ͼ���������߶�AB=2��CD=4����A�������ϱ�ʾ������-10����C�������ϱ�ʾ������16�����߶�AB��6����λ/����ٶ����������˶���ͬʱ�߶�CD��2����λ/����ٶ����������˶����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{��-4������-9��}$=$\sqrt{-4}$��$\sqrt{-9}$=6 | B�� | ��$\sqrt{3}$-1��2=3-1=2 | ||
| C�� | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{81}$��$\sqrt{1}$=9 | D�� | 3$\sqrt{\frac{2}{3}}$=$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | -2 | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 100cm2 | B�� | 200cm2 | C�� | 300cm2 | D�� | 400cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
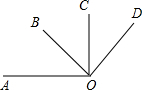 ��ͼ������AOD=120�㣬��BOC=70�㣬�ҡ�AOC����BOD=9��10�����AOB=20�㣮
��ͼ������AOD=120�㣬��BOC=70�㣬�ҡ�AOC����BOD=9��10�����AOB=20�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | sinA=cosB | B�� | sinA=sinB | C�� | cosA=cosB | D�� | sinB=cosB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2.6��105 | B�� | 26��104 | C�� | 2.6��104 | D�� | 0.26��106 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com