
青岛市2009年模拟练习
高中数学(理科) 2009.05
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
注意事项:
1.答卷前,考生务必用2B铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.
3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合 ,则
,则
A. B.
B. C.
C. D.
D.
2.
 为虚数单位
为虚数单位 的二项展开式中第七项为
的二项展开式中第七项为
A. B.
B. C.
C. D.
D.
3. 设 都是非零向量,那么命题“
都是非零向量,那么命题“ 与
与 共线”是命题“
共线”是命题“ ”的
”的
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
 4.如右图为长方体木块堆成的几何体的三视图,
4.如右图为长方体木块堆成的几何体的三视图,
则组成此几何体的长方体木块块数共有
A.3块 B.4块 C.5块 D.6块
5. 已知各项不为 的等差数列
的等差数列 ,满足
,满足
 ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则
A. B.
B. C.
C. D.
D.
6.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程 看作时间
看作时间 的函数,其图象可能是
的函数,其图象可能是
 |
7. 已知双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则双曲线的离心率为
,则双曲线的离心率为
 A.
A. B.
B. C.
C. D.
D.
8.某程序框图如右图所示,现输入如下四个函数,则可以输出的函数是
A.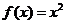 B.
B.
C. D.
D.
9.如右下图,在一个长为 ,宽为2的矩形
,宽为2的矩形 内,曲线
内,曲线 与
与 轴围成如图所示的阴影部分,向矩形
轴围成如图所示的阴影部分,向矩形 内随机投一点(该点落在矩形
内随机投一点(该点落在矩形 内任何一点是等可能的),则所投的点落在阴影部分的概率是
内任何一点是等可能的),则所投的点落在阴影部分的概率是
 A.
A. B.
B.  C.
C.
 D.
D.

10. 已知直线 平面
平面 ,直线
,直线 平面
平面 ,给出下列命题中
,给出下列命题中
① ∥
∥ ;②
;② ∥
∥ ;
;
③ ∥
∥ ;④
;④ ∥
∥
 .其中正确的是
.其中正确的是
A.①②③ B.②③④ C.②④ D.①③ 学
学
 11. 已知
11. 已知 船在灯塔
船在灯塔 北偏东
北偏东 且
且 到
到 的距离为
的距离为 ,
, 船在灯塔
船在灯塔 西偏北
西偏北 且
且 到
到 的距离为
的距离为 ,则
,则 两船的距离为
两船的距离为
A.
 B.
B.  C.
C.  D
D .
.
12.把3盆不同的兰花和4盆不同的玫瑰花摆放在右图图案中的
 所示的位置上,其中三盆兰花不能放在一条直线上,
所示的位置上,其中三盆兰花不能放在一条直线上,
则不同的摆放方法为
A. 种 B.
种 B. 种 C.
种 C. 种 D.
种 D. 种
种
网第Ⅱ卷(非选择题 共90分)
二、填空:本大题共4小题,每小题4分,共16分.
 |
则第 个图案中有白色地面砖的块数是
.
个图案中有白色地面砖的块数是
.
14.已知 ,则
,则 的值等于
.
的值等于
.
15.已知函数
 满足
满足 ,且
,且 时,
时, ,则
,则 与
与 的图象的交点个数为
.
的图象的交点个数为
. 学科网
学科网
16.若不等式 对于一切非零实数
对于一切非零实数 均成立,则实数
均成立,则实数 的取值范围是
的取值范围是
.
三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知向量 (
( 为常数且
为常数且 ),函数
),函数 在
在 上的最大值为
上的最大值为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)把函数 的图象向右平移
的图象向右平移 个单位,可得函数
个单位,可得函数 的图象,若
的图象,若 在
在 上为增函数,求
上为增函数,求 的最大值.
的最大值.
18. (本小题满分12分)
某种食品是经过 、
、 、
、 三道工序加工而成的,
三道工序加工而成的, 、
、 、
、 工序的产品合格率分别为
工序的产品合格率分别为 、
、 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
(Ⅰ)正式生产前先试生产 袋食品,求这2袋食品都为废品的概率;
袋食品,求这2袋食品都为废品的概率;
(Ⅱ)设 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求 的分布列和数学期望.
的分布列和数学期望.
19.(本小题满分12分)
 如图1所示,在边长为
如图1所示,在边长为 的正方形
的正方形 中,
中,
 ,且
,且 ,
, ,
, 分别交
分别交
 于点
于点 ,将该正方形沿
,将该正方形沿 、
、 折叠,使得
折叠,使得 与
与 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱 中
中
(Ⅰ)求证:
 ;
;
(Ⅱ)在底边 上有一点
上有一点 ,
, ,
,
求证: 面
面
(III)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
20.(本小题满分12分)
在数列 中,
中, .
.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)设数列 满足
满足 ,若
,若
 对一切
对一切 且
且 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
21.(本小题满分12分)已知函数 ,直线
,直线 与函数
与函数 图象相切.
图象相切.
(Ⅰ)求直线 的斜率
的斜率 的取值范围;
的取值范围;
(Ⅱ)设函数 ,已知函数
,已知函数 的图象经过点
的图象经过点 ,求函数
,求函数 的极值.
的极值.
22. (本小题满分14分)已知两点 ,点
,点 为坐标平面内的动点,且满足
为坐标平面内的动点,且满足 .
.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线 斜率为
斜率为 ,且与曲线
,且与曲线 相交于点
相交于点 、
、 ,若
,若 、
、 两点只在第二象限内运动,线段
两点只在第二象限内运动,线段 的垂直平分线交
的垂直平分线交 轴于
轴于 点,求
点,求 点横坐标的取值范围.
点横坐标的取值范围.
青岛市2009年模拟练习
数学(理科)答案及评分标准 2009.05
CABBD,AADAD,BB
二、填空:本大题共4小题,每小题4分,共16分.
13. ; 14.
; 14. ;
; 学科网 15.
学科网 15. ; 16.
; 16.
三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)
解:(Ⅰ) ………3分
………3分
因为函数 在
在 上的最大值为
上的最大值为 ,所以
,所以 故
故 …………5分
…………5分
(Ⅱ)由(Ⅰ)知:
把函数 的图象向右平移
的图象向右平移 个单位,
个单位,
可得函数 …………………………………………8分
…………………………………………8分
又
 在
在 上为增函数
上为增函数
 的周期
的周期 即
即
所以 的最大值为
的最大值为 …………………………12分
…………………………12分
18. (本小题满分12分)
解:(Ⅰ)2袋食品都为废品的情况为
①2袋食品的三道工序都不合格
 ……………2分
……………2分
②有一袋食品三道工序都不合格,另一袋有两道工序不合格
 ……………4分
……………4分
③两袋都有两道工序不合格

所以2袋食品都为废品的概率为 ……………6分
……………6分
(Ⅱ)


 ………8分
………8分

 ………10分
………10分










 ………12分
………12分
19.(本小题满分12分)
(Ⅰ)证明:因为 ,
, ,
,
所以 ,从而
,从而 ,即
,即 .………………………2分
.………………………2分
又因为 ,而
,而 ,
,
所以
 平面
平面 ,又
,又 平面
平面
所以
 ;………………4分
;………………4分
(Ⅱ)解:过 作
作 交
交 于
于 ,连接
,连接 ,
,
因为


 ……………6分
……………6分


 四边形
四边形 为平行四边形
为平行四边形
 ,所以
,所以 平面
平面 …………………………8分
…………………………8分
(III)解:由图1知, ,分别以
,分别以 为
为 轴,
轴,
则


 ………10分
………10分
设平面 的法向量为
的法向量为 ,
,
所以 得
得 ,
,
令 ,则
,则 ,
,
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 …………………………12分
…………………………12分
20.(本小题满分12分)
解:(Ⅰ) 由 变形得:
变形得:
即
所以 …………………4分
…………………4分
故数列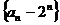 是以
是以 为首项,
为首项, 为公差的等差数列………………………5分
为公差的等差数列………………………5分
(Ⅱ)由(Ⅰ)得 …………………………6分
…………………………6分
所以 …………………………7分
…………………………7分
设 ………………8分
………………8分
则
两式相除得: ……10分
……10分
所以 是关于
是关于 的单调递增函数,则
的单调递增函数,则
故实数 的取值范围是
的取值范围是 …………………………12分
…………………………12分
21.(本小题满分12分)
解:(Ⅰ)设切点坐标为 ,
,  ………………………2分
………………………2分
则 …………………………4分
…………………………4分
根据题意知: ,即
,即 ,所以
,所以
又 ,则
,则 ,即
,即
所以 …………………………6分
…………………………6分
(Ⅱ)显然 的定义域为
的定义域为 ………7分
………7分
则 ………………………8分
………………………8分
又因为函数 的图象经过点
的图象经过点 ,代入
,代入
求得: ,则
,则 ……………10分
……………10分
由此可知:当 时,有
时,有 ,此时
,此时 为单调增函数;
为单调增函数;
当 时,有
时,有 ,此时
,此时 为单调减函数;
为单调减函数;
所以 在区间
在区间 上只有极大值即
上只有极大值即 …12分
…12分
22. (本小题满分14分)
解:(Ⅰ)设点 ,根据题意则有:
,根据题意则有:

代入 得:
得: …………3分
…………3分
整理得点 的轨迹
的轨迹 的方程
的方程 …………………………5分
…………………………5分
(Ⅱ)设
由题意得: 的方程为
的方程为 (显然
(显然 )
)
与 联立消元得:
联立消元得: …………………………7分
…………………………7分
则有:
因为直线交轨迹 于两点,则
于两点,则 ,
,
再由 ,则
,则 ,故
,故 ………………………8分
………………………8分
可求得线段 中点
中点 的坐标为
的坐标为
所以线段 的垂直平分线方程为
的垂直平分线方程为 …………………………10分
…………………………10分
令 得点
得点 横坐标为
横坐标为 …………………………………12分
…………………………………12分


所以 点横坐标的取值范围为
点横坐标的取值范围为 …………14分
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com