
金堂中学高2009级数学定时训练题(二)
姓名 成绩 (考试时间80分钟)
一、选择题(每题5分,共50分)
1、设集合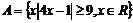 ,
, 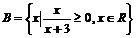 , 则A∩B= ( )
, 则A∩B= ( )
A.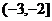 B.
B.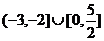 C.
C.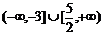 D.
D.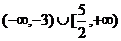
2、集合A={x|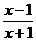 <0=,B={x || x -b|<a
<0=,B={x || x -b|<a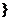 ,若“a=1”是“A∩B≠
,若“a=1”是“A∩B≠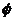 ”的充分条件, 则b的取值范围是 ( )
”的充分条件, 则b的取值范围是 ( )
A.-2≤b<0 B.0<b≤2 C.-3<b<-1 D.-1≤b<2
3、(理科)复数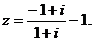 在复平面内,z所对应的点在 (
)
在复平面内,z所对应的点在 (
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(文科)函数y=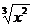 -1(X≤0)的反函数是 ( )
-1(X≤0)的反函数是 ( )
(A)y=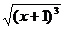 (x≥-1) (B)y= -
(x≥-1) (B)y= -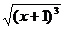 (x≥-1)
(x≥-1)
(C) Y=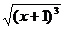 (x≥0)
(d)Y= -
(x≥0)
(d)Y= -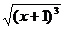 (x≥0)
(x≥0)
4、若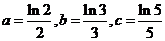 ,则
( )
,则
( )
(A)a<b<c (B)c<b<a (C)c<a<b (D)b<a<c
5、若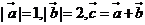 ,且
,且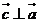 ,则向量
,则向量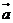 与
与 的夹角为
( )
的夹角为
( )
(A)30° (B)60° (C)120° (D)150°
6、(理科)函数f(x)=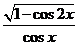 ( )
( )
(A)在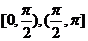 上递增,在
上递增,在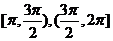 上递减
上递减
(B)在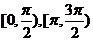 上递增,在
上递增,在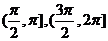 上递减
上递减
(C)在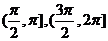 上递增,在
上递增,在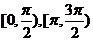 上递减
上递减
(D)在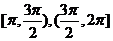 上递增,在
上递增,在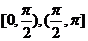 上递减
上递减
(文科)点O是三角形ABC所在平面内的一点,满足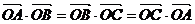 ,则点O是△ABC的
(
)
,则点O是△ABC的
(
)
A.三个内角的角平分线的交点 B.三条边的垂直平分线的交点
C.三条中线的交点 D.三条高的交点
7、已知正四棱锥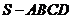 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 是
是 的中点,则
的中点,则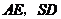 所成的角的余弦值为
( )
所成的角的余弦值为
( )
A.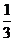 B.
B.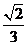 C.
C.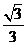 D.
D.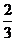
8、从20名男同学,10名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为 ( )
A.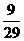 B.
B.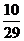 C.
C.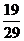 D.
D.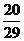
9、(理科)设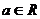 ,若函数
,若函数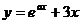 ,
,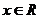 有大于零的极值点,则 ( )
有大于零的极值点,则 ( )
A.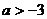 B.
B. 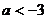 C.
C. 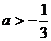 D.
D. 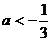
(文科)设P为曲线C: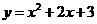 上的点,且曲线C在点P处切线
上的点,且曲线C在点P处切线
倾斜角的取值范围为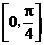 ,则点P横坐标的取值范围为
( )
,则点P横坐标的取值范围为
( )
A.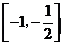 B.
B.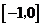 C.
C.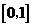 D.
D.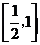
10、若直线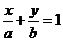 通过点
通过点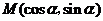 ,则
( )
,则
( )
A.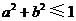 B.
B.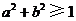 C.
C.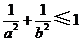 D.
D.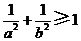
二、填空题(每题4分,共16分)
11、设向量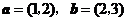 ,若向量
,若向量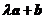 与向量
与向量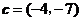 共线,则
共线,则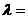
12、(理科)在数列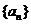 在中,
在中,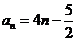 ,
,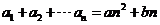 ,
,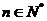 ,其中
,其中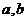 为常数,则
为常数,则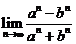 的值是
的值是
(文科)在数列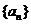 在中,
在中,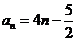 ,
,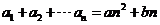 ,
,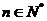 ,其中
,其中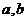 为常数,则
为常数,则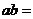
13、某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有 种.(用数字作答).
14、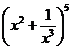 的展开式中常数项为 ;各项系数之和为
.(用数字作答)
的展开式中常数项为 ;各项系数之和为
.(用数字作答)
二、解答题:(共34分)
15、(10分)在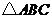 中,
中,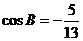 ,
,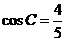 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设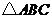 的面积
的面积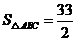 ,求
,求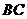 的长.
的长.
17、(12分)(理科)设函数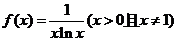
(Ⅰ)求函数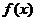 的单调区间;
的单调区间;
(Ⅱ)已知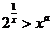 对任意
对任意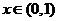 成立,求实数
成立,求实数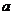 的取值范围。
的取值范围。
(文科)设函数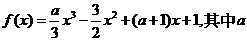 为实数。
为实数。
(Ⅰ)已知函数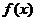 在
在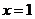 处取得极值,求
处取得极值,求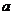 的值;
的值;
(Ⅱ)已知不等式 对任意
对任意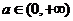 都成立,求实数
都成立,求实数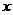 的取值范围。
的取值范围。
18、(12分)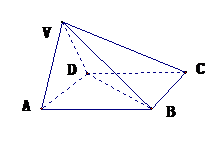 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)证明AB⊥平面VAD.
(Ⅱ)求面VAD与面VDB所成的二面角的大小.
1、D 2、D 3、(理)B(文)4、C 5、C 6、(理)A(文)D 7、C 8、D 9、(理)B(文)A
10、D
二、填空题
11、2 12、(理)1(文)―1 13、96 14、10、32
三、解答题
15、解:(Ⅰ)由 ,得
,得 ,
,
由 ,得
,得 .
.
所以 .??????????????????????????????????????????? 5分
.??????????????????????????????????????????? 5分
(Ⅱ)由 得
得 ,
,
由(Ⅰ)知 ,
,
故 ,??????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
,??????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
又 ,
,
故 ,
, .
.
所以 .????????????????????????????????????????????????????????????????????????????????????? 10分
.????????????????????????????????????????????????????????????????????????????????????? 10分
17、(理)解: (1)  若
若  则
则  列表如下
列表如下






+
0
-
-

单调增
极大值
单调减
单调减
(2) 在  两边取对数, 得
两边取对数, 得  ,由于
,由于 所以
所以
 (1)
(1)
由(1)的结果可知,当 时,
时,  ,
,
为使(1)式对所有 成立,当且仅当
成立,当且仅当 ,即
,即
(文)解:(1)  ,由于函数
,由于函数 在
在 时取得极值,所以
时取得极值,所以 
即 
(2) 方法一:由题设知: 对任意
对任意 都成立
都成立
即 对任意
对任意 都成立
都成立
设  , 则对任意
, 则对任意 ,
, 为单调递增函数
为单调递增函数
所以对任意 ,
, 恒成立的充分必要条件是
恒成立的充分必要条件是
即  ,
,
于是 的取值范围是
的取值范围是
18、解:证明:(Ⅰ)作AD的中点O,则VO⊥底面ABCD.…………………………1分
建立空间直角坐标系,并设正方形边长为1,…………………………2分
则A( ,0,0),B(
,0,0),B( ,1,0),C(-
,1,0),C(- ,1,0),
,1,0),
D(- ,0,0),V(0,0,
,0,0),V(0,0, ),
),
∴ ………………………………3分
………………………………3分
由 ……………………………………4分
……………………………………4分
 ……………………………………5分
……………………………………5分
又AB∩AV=A
∴AB⊥平面VAD…………………………………………………………………………6分
(Ⅱ)由(Ⅰ)得 是面VAD的法向量………………………………7分
是面VAD的法向量………………………………7分
设 是面VDB的法向量,则
是面VDB的法向量,则
 ……9分
……9分
∴ ,……………………………………11分
,……………………………………11分
又由题意知,面VAD与面VDB所成的二面角,所以其大小为 …………12分
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com