
山东省都进中学2009届高三年级第三次模拟考试
数学理科卷 2009.03
注意事项:
1.本试题分为第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间为120分钟.
2.答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上.考试结束,试题
和答题卡一并收回.
3.第Ⅰ卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)
涂黑,如需改动,必须先用橡皮擦干净,再改涂其它答案.
第Ⅰ卷 (共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有
1.设复数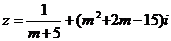 为实数时,则实数
为实数时,则实数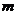 的值是 ( )
的值是 ( )
A.3
B.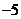 D.
D.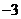 或5
或5
2.函数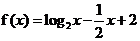 的零点个数为 ( )
的零点个数为 ( )
A.0 B.
3.若集合 ,
,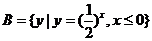 ,则
,则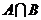 等于 ( )
等于 ( )
A.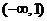 B.
B.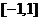 C.
C.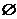 D.{1}
D.{1}
4.设m<0,两直线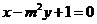 与
与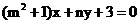 垂直,则
垂直,则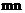 的最大值为( )
的最大值为( )
A.-2 B.
5.运载“神州七号”宇宙飞船的火箭在点火第一分钟通过的路程为
程增加
时间是 ( )
A.10分钟 B.12分钟 C.15分钟 D.18分钟
6.在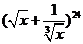 的展开式中,
的展开式中,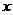 的幂的指数是整数的项共有 ( )
的幂的指数是整数的项共有 ( )
A.3项 B.4项 C.5项 D.6项
7.已知函数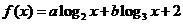 ,若
,若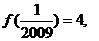 则
则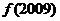 的值是 ( )
的值是 ( )
A.-4 B.
8.若函数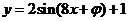 的图象关于直线
的图象关于直线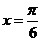 对称,则
对称,则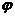 的值是 ( )
的值是 ( )
A.0 B.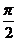 C.
C.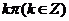 D.
D.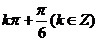
9.把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数
为b,设向量 则向量
则向量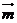 与向量
与向量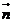 垂直的概率为 ( )
垂直的概率为 ( )
A.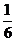 B.
B.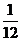 C.
C.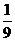 D.
D.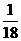
10.已知变量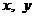 满足
满足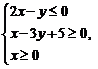 则
则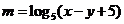 的最大值为 ( )
的最大值为 ( )
A.4
B.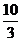
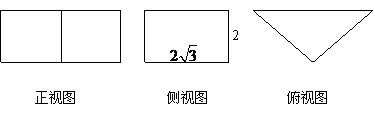
11.若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为 ( )
 C.
C.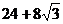 D.
D.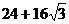
12.右图是计算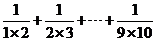 的值算法框图,
的值算法框图,
其中在判断框中应填入的条件是 ( )
A.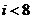 B.
B.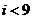
C.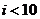 D.
D.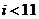
第Ⅱ卷
把答案填在横线上.
二、填空题:本大题共5小题,每小题4分,共20分.
13.已知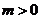 ,若
,若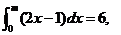 则
则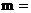 .
.
14.在直角坐标系中,点A在圆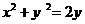 上,点B在直线
上,点B在直线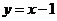 上,则
上,则 的最小
的最小
值为 .
15.已知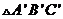 是水平放置的边长为a的正三角形ABC的斜二测平面直观图,那么
是水平放置的边长为a的正三角形ABC的斜二测平面直观图,那么
16.右图是2008年“华东”杯第13届CCTV青年歌手电视大奖赛上某位
选手得分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据
的方差为 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)已知函数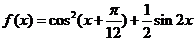 .
.
(1)求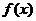 的最值;
的最值;
(2)求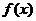 的单调增区间.
的单调增区间.
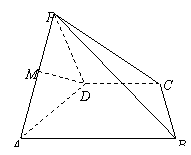
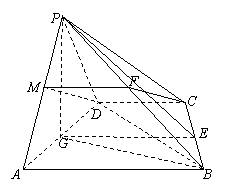
18.(本小题满分12分)如图,四棱锥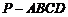 中,底面
中,底面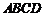 是直角梯形,
是直角梯形,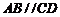 ,
,
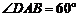 ,
,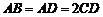 ,侧面
,侧面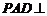 底面
底面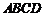 ,且
,且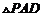 为等腰直角三角
为等腰直角三角
 形,
形,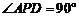 ,
,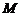 为
为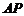 的中点.
的中点.
(1)求证: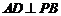 ;
;
(2)求证: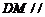 平面
平面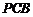 ;⑶求二面角
;⑶求二面角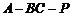 的正切值.
的正切值.
19、(本小题满分12分)在一次考试中共有8道选择题,每道选择题都有4个选项,其中有
且只有一个选项是正确的.评分标准规定:“每题只选一个选项,选对得5分,不选或
选错得0分”.某考生已确定有4道题答案是正确的,其余题中:有两道只能分别判断2
个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,
求:
(1)该考生得40分的概率;
(2)该考生得多少分的可能性最大?⑶该考生所得分数的数学期望.
20.(本小题满分12分)已知数列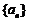 中,
中,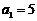 ,
,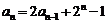 (
(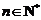 且
且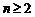 ).
).
(1)若数列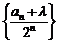 为等差数列,求实数
为等差数列,求实数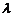 的值;
的值;
(2)求数列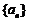 的前
的前 项和
项和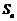 .
.
21.(本小题满分12分)设函数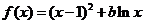 ,其中
,其中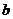 为常数.
为常数.
(1)当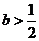 时,判断函数
时,判断函数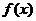 在定义域上的单调性;
在定义域上的单调性;
(2)若函数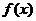 的有极值点,求
的有极值点,求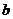 的取值范围及
的取值范围及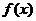 的极值点.
的极值点.
22.(本小题满分14分)已知椭圆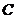 的方程为
的方程为
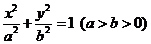 ,过其左焦点
,过其左焦点
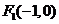 ,斜率为1的直线交椭圆于
,斜率为1的直线交椭圆于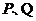 两点.
两点.
(1)若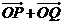 与
与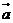 =(-3,1)共线,求椭圆C的方程;
=(-3,1)共线,求椭圆C的方程;
(2)已知直线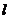 :
: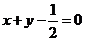 ,在
,在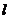 上求一点
上求一点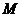 ,使以椭圆的焦点为焦点且过
,使以椭圆的焦点为焦点且过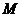 点
点
的双曲线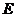 的实轴最长,求点
的实轴最长,求点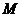 的坐标和此双曲线
的坐标和此双曲线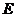 的方程。
的方程。
参 考 答 案
一、选择题
1.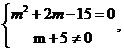 解得
解得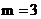 .
.
2.函数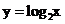 与
与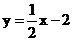 的图象有两个交点,故
的图象有两个交点,故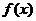 有两个零点.
有两个零点.
3.集合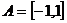 ,集合
,集合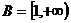 ,
,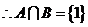 .
.
4.由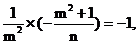 得
得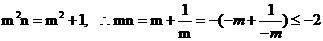 .
.
5.设这一过程大约需要t分钟,火箭发射后每分钟通过的路程分别为
一等差数列,根据等差数列求和公式得: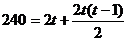 ,即
,即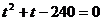 ,解
,解
得: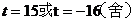 .
.
6.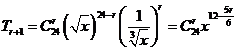 ,故当
,故当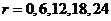 时,幂指数为整数,共5项.
时,幂指数为整数,共5项.
7.由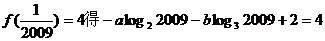 ,
,
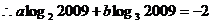 .
.
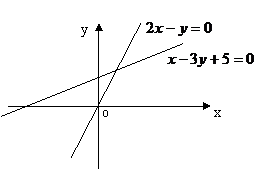
 .
.
8.由题知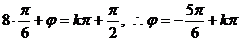 ,即选项D.
,即选项D.
9.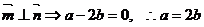 ,满足条件的
,满足条件的
有序实数对由(2,1),(4,2),(6,3),则垂
直的概率为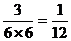 .
.
10.求目标函数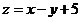 的最大值,如图所示,可知
的最大值,如图所示,可知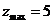 ,所以
,所以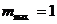 .
.
11.有三视图可知该正三棱柱底面正三角形的高为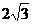 ,棱柱高为2,可得底面边长为4,从而
,棱柱高为2,可得底面边长为4,从而
可求得棱柱的表面积.
12.此结构为直到型循环结构,当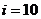 时停止循环。
时停止循环。
二、填空题
13.3 解析: 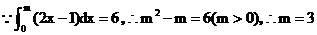 .
.
14.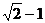 解析:圆心坐标为(0,1)到直线
解析:圆心坐标为(0,1)到直线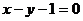 的距离为
的距离为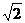 ,圆的半径为1,
,圆的半径为1,
故所求最小距离为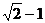 .
.
15.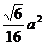 解析:
解析: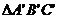 的高为
的高为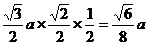 ,所以面积为
,所以面积为
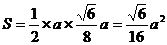 .
.
16.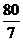 解析:根据方差计算公式可得.
解析:根据方差计算公式可得.
三、解答题
17.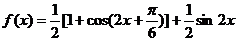 ------------- 2分
------------- 2分
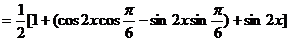
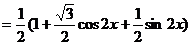 --------------------4分
--------------------4分
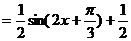 ------------------------6分
------------------------6分
(1)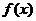 的最大值为
的最大值为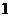 、最小值为
、最小值为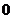 ;---------------------- 8分
;---------------------- 8分
(2)由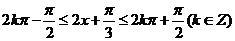 , ----------- 10分
, ----------- 10分
得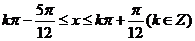 ,
,
从而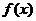 的单调增区间为
的单调增区间为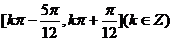 ----------12分
----------12分
18.解法一:(1)取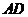 的中点
的中点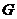 ,连结
,连结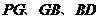
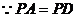 ,
,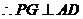 --------------2分
--------------2分
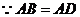 ,且
,且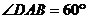 ,
,
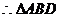 是正三角形,
是正三角形,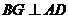 . ------ 3分
. ------ 3分
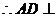 平面
平面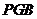
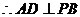 . ---------------- 4分
. ---------------- 4分
(2)取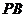 的中点
的中点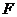 ,联结
,联结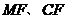 ,
,
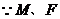 分别为
分别为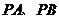 的中点,
的中点,
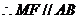 ,且
,且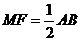 ----------- 6分
----------- 6分
∵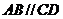 且
且 ,
,
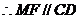 且
且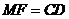 .
.
∴四边形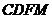 是平行四边形
是平行四边形
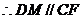 .
------------- 7分
.
------------- 7分
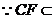 平面
平面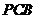 ,
,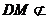 平面PCB,
平面PCB,
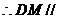 平面
平面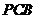 ---------------- 8分
---------------- 8分
(3)取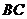 的中点
的中点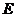 ,联结
,联结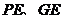
∵四边形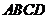 是直角梯形且
是直角梯形且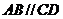 ,
,
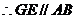 ,
,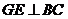 ,
,
又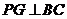 ,
,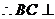 平面
平面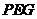 ,
,
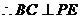 ,
,
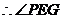 是二面角
是二面角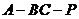 的平面角. -------------10分
的平面角. -------------10分
设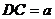 ,则
,则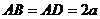 ;
;
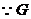 、
、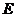 分别为
分别为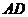 、
、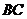 中点,
中点,
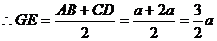
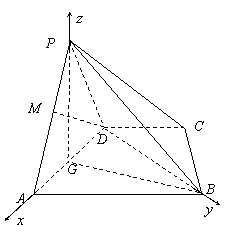
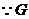 是等腰直角三角形
是等腰直角三角形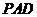 斜边的中点,
斜边的中点,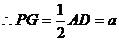 -----------11分
-----------11分
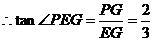 ,
,
∴二面角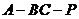 的正切值为
的正切值为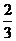 ---------------12分
---------------12分
解法二:(1)同解法1;
(2)∵侧面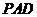
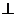 底面
底面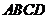 ,
,
又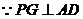 ,
,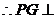 底面
底面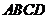
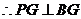
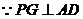
∴直线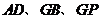 两两互相垂直,故可以分别以直线
两两互相垂直,故可以分别以直线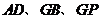 为
为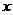 轴、
轴、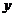 轴
轴
和 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系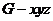 . -------5分
. -------5分
设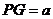 ,则可求得
,则可求得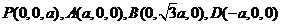 ,则
,则
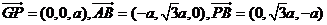 .
.
设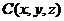 ,则
,则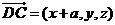 ,
,
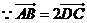 ,
,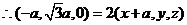 ,
,
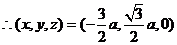 ,即
,即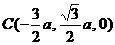
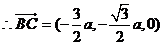 ----------6分
----------6分
设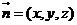 是平面
是平面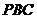 的法向量,则
的法向量,则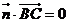 且
且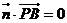 ,
,
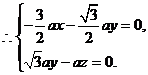
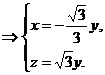
取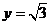 ,得
,得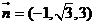 -----------------7分
-----------------7分
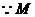 是
是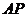 的中点,
的中点,
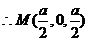
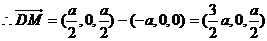
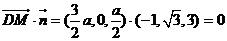 ,
,
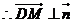 ------------8分
------------8分
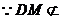 平面
平面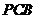
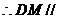 平面
平面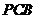 ---------------9分
---------------9分
(3)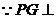 平面
平面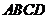 ,
, 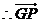 是平面
是平面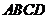 的法向量,
----------10分
的法向量,
----------10分
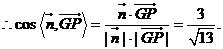 ------------11分
------------11分
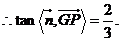 ∴二面角
∴二面角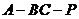 的正切值为
的正切值为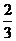 ------------12分
------------12分
19.解:(1)设选对一道“可判断2个选项是错误的”题目为事件A,“可判断1个选项是错误
的”该题选对为事件B,“不能理解题意的”该题选对为事件C.则
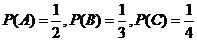 ------------2分
------------2分
所以得40分的概率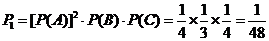 ---------3分
---------3分
(2)该考生得20分的概率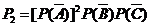 =
=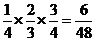 --------4分
--------4分
该考生得25分的概率
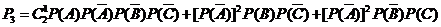
=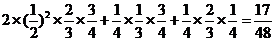 -----------6分
-----------6分
该考生得30分的概率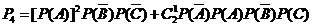
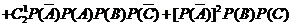
=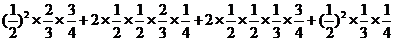 =
=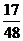 -----------8分
-----------8分
该考生得35分的概率
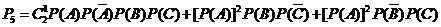
=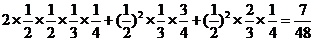
∵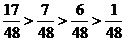 ∴该考生得25分或30分的可能性最大------10分
∴该考生得25分或30分的可能性最大------10分
(3)该考生所得分数的数学期望
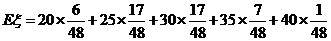 =
=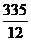 ---------12分
---------12分
20.(1)因为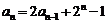 (
(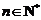 且
且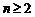 ),
),
所以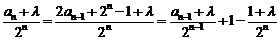 ----------2分
----------2分
显然,当且仅当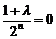 ,即
,即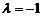 时,数列
时,数列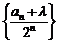 为等差数列;---5分
为等差数列;---5分
(2)由(1)的结论知:数列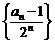 是首项为
是首项为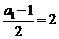 ,公差为1的等差数列,
,公差为1的等差数列,
故有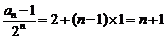 ,-------6分
,-------6分
即 (
(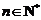 )--------7分
)--------7分
因此,有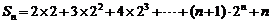 ,
,
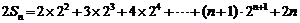 ,------9分
,------9分
两式相减,得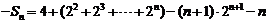 ,-----10分
,-----10分
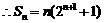 (
(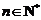 )-----------------12分
)-----------------12分
21.(1)由题意知,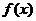 的定义域为
的定义域为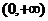 ,
,
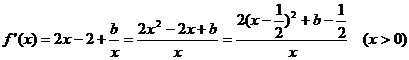 --------- 2分
--------- 2分
 当
当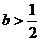 时,
时,
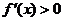 ,函数
,函数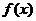 在定义域
在定义域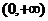 上单调递增 ------ 4分
上单调递增 ------ 4分
(2)①当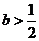 时,由(1)知函数
时,由(1)知函数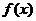 在
在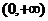 上单调,无极值点; -------5分
上单调,无极值点; -------5分
②当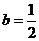 时,
时,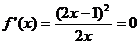 有两个相同的解
有两个相同的解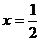 ,
,
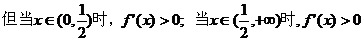 时,
时,
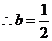 时,函数
时,函数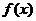 在
在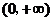 上无极值点 -----------
6分
上无极值点 -----------
6分
③当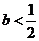 时,
时,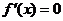 有两个不同解:
有两个不同解:
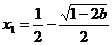
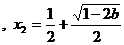 ---7分
---7分
若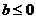 ,则
,则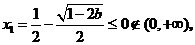
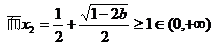 ,此时
,此时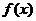 随
随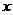 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
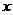
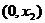
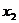
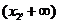
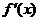

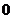
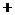
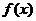
减
极小值
增
由表可知: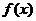 有惟一极小值点
有惟一极小值点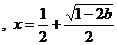 , -----9分
, -----9分
若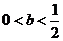 ,则0<
,则0<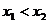 <1,此时,
<1,此时,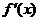 ,
,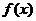 随
随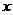 的变化情况如下表:
的变化情况如下表:
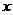
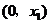
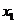
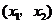
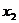
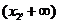
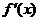
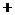
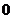

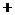
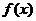
增
极大值
减
极小值
增
由表可知: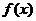 有一个极大值点
有一个极大值点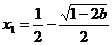 和一个极小值点
和一个极小值点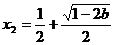 ;
-------11分
;
-------11分
综上所述:b的范围是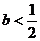 .
.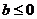 时,
时,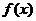 有惟一最小值点
有惟一最小值点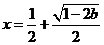 ;
;
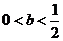 时,
时,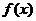 有一个极大值点
有一个极大值点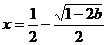 和一个极小值点
和一个极小值点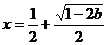 ------ 12分
------ 12分
22.(1)将直线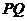 的方程为:
的方程为: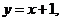 代入
代入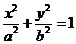 ,可得:
,可得:
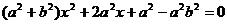 ;
;
令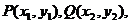 则
则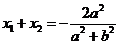 ---------2分
---------2分
由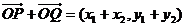 ,
,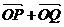 与
与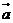 =(-3,1)共线,得
=(-3,1)共线,得
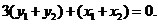 ∴
∴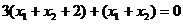 ,
,
∴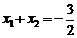 ,即
,即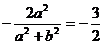 ,∴
,∴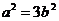 ; --------- 4分
; --------- 4分
又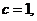
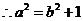 ,∴
,∴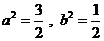 ,所以椭圆C的方程为
,所以椭圆C的方程为 ;---6分
;---6分
(2)椭圆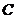 的右焦点为
的右焦点为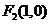 ,
,
直线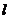 的方程为:
的方程为: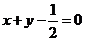 ,因为
,因为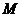 在双曲线
在双曲线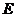 上,要双曲线
上,要双曲线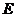 的实轴最长,只
的实轴最长,只
须 最大,
----------------- 8分
最大,
----------------- 8分
设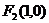 关于直线
关于直线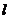 的对称点为
的对称点为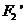 ,则可求
,则可求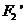 (
(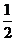 ,-
,-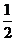 ),
),
则直线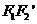 与直线
与直线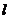 的交点为所求
的交点为所求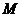 ,---------------------------------10分
,---------------------------------10分
易得直线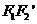 :
: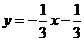 ,由
,由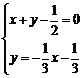 ,得M(
,得M(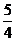 ,-
,-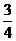 );------ 12分
);------ 12分
故双曲线的长轴最长为: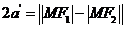
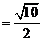 ,
,
∴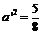 ,又
,又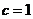 ,
,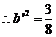 ,
,
故所求双曲线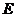 方程为:
方程为:
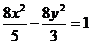 .
----------- 14分
.
----------- 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com