联合命题 由 石门一中;澧县一中;郴州一中;益阳市一中;桃源县一中;株洲市二中
试题详情
二、选择题:(本大题共8小题,每小题5分,共40分。下列各小题所给出的四个答案中只有一个是正确的) 1、 复数 复数 表示纯虚数的条件为
( C ) 表示纯虚数的条件为
( C ) 试题详情
试题详情
2、一小孩在三角形ABC的三个顶点之间玩跳棋游戏,若此棋子从A点起跳,移动4次后仍回到A点,则此棋子不同的跳法的种数是 A.4
B.5
C.6
D.7
( C ) 试题详情
试题详情
试题详情
4、我们知道,平面几何中有些正确的结论在空间中不一定成立.下面给出的平面几何中的四个真命题: ①平行于同一条直线的两条直线必平行; ②垂直于同一条直线的两条直线必平行; ③一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补; ④一个角的两边分别垂直于另一个角的两边,那么这两个角相等或互补. 在空间中仍然成立的有
( D ) A. ②③
B. ①④
C. ②④ D.①③ 试题详情
5、已知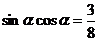 ,且 ,且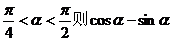 的值是 ( B ) 的值是 ( B ) 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
 二、填空题:(本大题7小题,每小题5分,共35分) 二、填空题:(本大题7小题,每小题5分,共35分)
试题详情
试题详情
试题详情
 11、函数 11、函数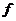 由下表定义 由下表定义
试题详情

1 2 3 4 5 试题详情

4 1 3 5 2 试题详情
若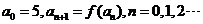 ,则 ,则 的值为
.
2 的值为
.
2 试题详情
 12、从 12、从 中,可得到一般规律为 中,可得到一般规律为
试题详情
  (用数学表达式表示) (用数学表达式表示)
试题详情
试题详情
试题详情
试题详情
  。
16
。
16
试题详情
试题详情
试题详情
 乙说:“不等式两边同除以 乙说:“不等式两边同除以 2,再作分析”. 2,再作分析”.
试题详情
 丙说:“把字母 丙说:“把字母 单独放在一边,再作分析”. 单独放在一边,再作分析”.
试题详情
试题详情
试题详情
试题详情
 三、解答题:(本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算过程.) 三、解答题:(本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算过程.)
 16、(本小题满分12分) 16、(本小题满分12分)
试题详情
试题详情
 (1)
求角B的取值范围; (1)
求角B的取值范围;
试题详情
试题详情
试题详情
试题详情
 (2 ) (2 ) 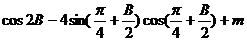
试题详情
 = =
试题详情
 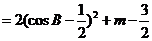 ……………………………………………………8分 ……………………………………………………8分
试题详情
试题详情
试题详情
试题详情
试题详情
 17、(本题满分12分) 17、(本题满分12分)
试题详情
 某高等学校自愿献血的50位学生的血型分布的情况如下表: 某高等学校自愿献血的50位学生的血型分布的情况如下表:
试题详情

血型 A B AB O 人数 20 10 5 15 (Ⅰ)从这50位学生中随机选出2人,求这2人血型都为A型的概率; 试题详情
 (Ⅱ)从这50位学生中随机选出2人,求这2人血型相同的概率; (Ⅱ)从这50位学生中随机选出2人,求这2人血型相同的概率;
试题详情
试题详情
 解:(Ⅰ)记“这2人血型都为A型”为事件A,那么
解:(Ⅰ)记“这2人血型都为A型”为事件A,那么 , ,
试题详情
 即这2人血型都为A型的概率是 即这2人血型都为A型的概率是 .
┅┅┅┅4分 .
┅┅┅┅4分
试题详情
 (Ⅱ)记“这2人血型相同”为事件B,那么 (Ⅱ)记“这2人血型相同”为事件B,那么 , ,
试题详情
 所以这2人血型相同的概率是 所以这2人血型相同的概率是 .
┅┅┅┅8分 .
┅┅┅┅8分
试题详情
试题详情
试题详情
 所以 所以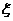 的分布列是 的分布列是
试题详情
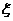
0 1 2 试题详情
试题详情
试题详情
试题详情
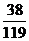
………..10分 试题详情
试题详情
试题详情
试题详情
 18、(本题满分12分) 18、(本题满分12分)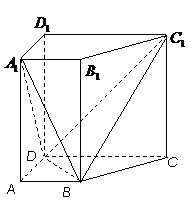
试题详情
试题详情
试题详情
试题详情
 (II)求二面角 (II)求二面角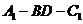 的余弦值. 的余弦值.
试题详情
 18.(本题满分12分) 18.(本题满分12分)
试题详情
 解法一: 解法一:
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
 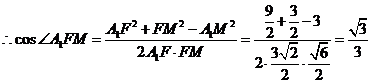 . .
试题详情
试题详情
 解法二: 解法二:
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
  ,
………..12分 ,
………..12分
试题详情
试题详情
 19、(本题满分13分) 19、(本题满分13分)
试题详情
试题详情
 (1)求椭圆 (1)求椭圆 的方程; 的方程;
试题详情
试题详情
 19.解:(1)依题意知, 19.解:(1)依题意知, …… 2分
…… 2分
试题详情
试题详情
试题详情
试题详情
 ∴ ∴  …… 8分 …… 8分
试题详情
解得: , ,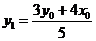 .
…… 9分 .
…… 9分 试题详情
∴ .
…… 11分 .
…… 11分 试题详情
试题详情
∴ 的取值范围为 的取值范围为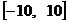 .
……13分 .
……13分 试题详情
试题详情
(2)求数列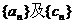 的通项公式; 的通项公式; 试题详情
(3)若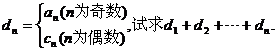 试题详情
20、解:(1)由 而 而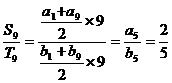 试题详情
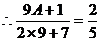 解得A=1
……………………………………3分 解得A=1
……………………………………3分
试题详情
试题详情
当n=1时,a1=S1=2,当n≥2时,an=Sn-Sn-1=n2+n 综合之:an=2n
…………………………………………6分 试题详情
由题意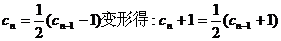 试题详情
∴数列{cn+1}是 为公比,以 为公比,以 为首项的等比数列。 为首项的等比数列。 试题详情
 ………………………9分
………………………9分
试题详情
(3)当 试题详情
试题详情
 ………………………11分
………………………11分
试题详情
当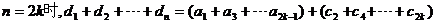 试题详情
试题详情
综合之: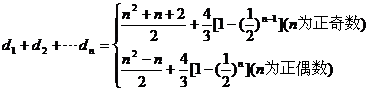 …………………13分 试题详情
试题详情
已知函数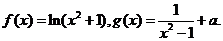 试题详情
试题详情
试题详情
(6) 求方程 的根的个数. 的根的个数. 试题详情
试题详情
试题详情
(2)由 得 得 , , 试题详情
故 仅有一个极小值点 仅有一个极小值点 ,根据题意得: ,根据题意得: 试题详情
试题详情
(3)令 试题详情
试题详情
当 时, 时, 试题详情
当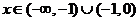 时, 时, 试题详情
试题详情
在 时, 时, 单调递增. ……………………………10分 单调递增. ……………………………10分 试题详情
试题详情
试题详情
试题详情
故 的根的情况为: 的根的情况为: 试题详情
当 时,即 时,即 时,原方程有2个根; 时,原方程有2个根; 试题详情
当 时,即 时,即 时,原方程有3个根; 时,原方程有3个根; 试题详情
当 时,即 时,即 时,原方程有4个根.
……………………………13分 时,原方程有4个根.
……………………………13分 试题详情
| 