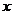|
试题详情
A.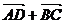 B. B. 试题详情
C.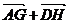 D. D. 试题详情
2.下列说法正确的是 ( B ) A.方向相同或相反的向量是平行向量 B.零向量的长度为0 C.长度相等的向量叫相等向量 D.共线向量是在同一条直线上的向量 试题详情
3.在△ABC中,D、E、F分别BC、CA、AB的中点,点M是△ABC的重心,则 试题详情
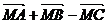 等于 ( C
) 等于 ( C
) 试题详情
试题详情
试题详情
5.非零向量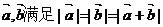 ,则 ,则 的夹角为 120° . 的夹角为 120° . 试题详情
6.在四边形ABCD中,若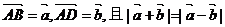 ,则四边形ABCD的形状是 ,则四边形ABCD的形状是 菱形
. 试题详情
试题详情
〖复习要求〗1、掌握平面向量的数量积及其几何意义,了解平面向量数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的充要条件。2、培养学生的化归思想、数形结合思想和分析问题、解决问题的能力。 〖双基回顾〗 (1).向量的夹角: 试题详情
试题详情
试题详情
其中?b?cos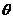 称为向量b在 称为向量b在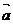 方向上的投影. 方向上的投影. (3).向量的数量积的性质: 试题详情
试题详情
试题详情
试题详情
试题详情
一、知识点训练:
试题详情
试题详情
试题详情
试题详情
试题详情
(4)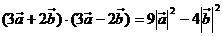 中,是真命题的有____ 中,是真命题的有____ A (1)(2) B
(2)(3) C (3)4) D
(2)4) 试题详情
试题详情
试题详情
试题详情
二、典型例题分析: 1、判断下列各命题正确与否;(1)若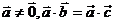 ,则 ,则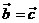 ;(2)若 ;(2)若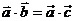 ,则 ,则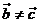 当且仅当 当且仅当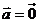 时成立;(3) 时成立;(3)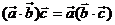 对任意向量 对任意向量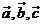 都成立;(4)对任一向量 都成立;(4)对任一向量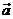 ,有 ,有 试题详情
2、三角形ABC中,A(-5,1),B(-1,7),C(1,2),求:(1)BC边上的中线AM的长。(2)∠CAB的平分线AD的长。(3)cos∠ABC的值。 试题详情
3、已知点A(1,2)和B(4,-1),问能否在 轴上找到一点C,使∠ACB=90°,若不能,说明理由,若能,求出C点坐标。 轴上找到一点C,使∠ACB=90°,若不能,说明理由,若能,求出C点坐标。 试题详情
试题详情
5、a、b为非零向量,当a + tb(tÎR)的模取最小值时,(1) 求t的值; (2)求证:b与a + tb垂直 试题详情
三、课堂练习: 1.设k∈R,下列向量中,与向量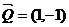 一定不平行的向量是 ( ) 一定不平行的向量是 ( ) 试题详情
试题详情
试题详情
坐标与 的坐标及 的坐标及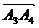 的坐标这和等于 ( ) 的坐标这和等于 ( ) A.(x4-x1,y4-y1) B.(x1-x4,y1-y4) C.(x3-x2,y3-y2) D.(x2-x4,y2-y3) 试题详情
3.已知平行四边形三个顶点的坐标分别为(-1,0),(3,0),(1,-5),则第四个点的坐 标为 ( ) A.(1,5)或(5,-5) B.(1,5)或(-3,-5) C.(5,-5)或(-3,-5) D.(1,5)或(-3,-5)或(5,-5) 试题详情
4.三点A(x1,y1),B(x2,y2),C(x3,y3)共线的主要条件是 ( ) A.x1y2-x2y1=0 B.(x2-x1)(y3-y1)=(x3-x1)(y2-y1) C.x1y3-x3y1=0
D.(x2-x1)(x3-x1)=(y2-y1)(y3-y1) 试题详情
试题详情
6.已知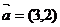 , ,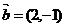 ,若 ,若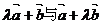 平行,则λ= ±1 . 平行,则λ= ±1 . (附1~5答案:C A D B A) 试题详情
§5.3 两点间的距离公式、线段的定比分点与图形的平移 试题详情
〖复习要求〗1、掌握两点间的距离公式及线段的定比分点和中点坐标公式,并能熟练应用。2、掌握平移公式。3、培养学生用化归思想解决问题的能力。 〖双基回顾〗 试题详情
1、P分有向线段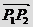 所成的比 所成的比 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
一、知识点训练: 1、已知A(-1,1),B(3,5),点P分有向线段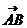 所成的比为 所成的比为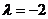 ,则点P的坐标为____ ,则点P的坐标为____ A (7,-9) B (-7,9) C (7,9) D (-7,-9) 试题详情
2、把函数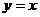 的图象F按 的图象F按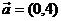 ,平移到F/,则F/的函数式为____ ,平移到F/,则F/的函数式为____ 试题详情
试题详情
3、设A、B、C三点共线,且它们的纵坐标分别为2,5,10,则A点分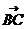 所得的比为_____ 所得的比为_____ 试题详情
试题详情
试题详情
试题详情
二、典型例题分析: 1、已知点A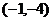 ,B(5,2),线段AB上的三等分点依次为 ,B(5,2),线段AB上的三等分点依次为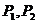 ,求 ,求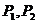 点的坐标以及A、B分 点的坐标以及A、B分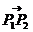 所成的比。 所成的比。 试题详情
2、求证:三角形三条中线交于一点,且交点与各顶点的距离等于所在中线长的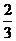 。 。 试题详情
3、函数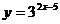 的图象按向量 的图象按向量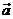 平移后,图象的解析式为 平移后,图象的解析式为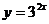 ,求向量 ,求向量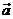 。 。 试题详情
4、设函数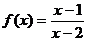 。 。 试题详情
(1) 试根据函数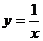 的图象作出 的图象作出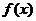 的图象,并写出交换过程; 的图象,并写出交换过程; 试题详情
(2) 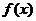 的图象是中心对称图形吗? 的图象是中心对称图形吗? 试题详情
(3) 指出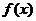 的单调区间。 的单调区间。 试题详情
试题详情
试题详情
则 试题详情
∵ 试题详情
∴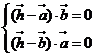 得 得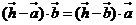 , , 试题详情
即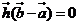 , ∴ , ∴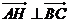 , , 试题详情
又∵点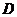 在 在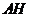 的延长线上, 的延长线上, 试题详情
∴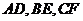 相交于一点。 相交于一点。 试题详情
三、课堂练习:
试题详情
试题详情
3、把一个函数的图象左移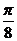 个单位,再向下平移2个单位得到的解析式为: 个单位,再向下平移2个单位得到的解析式为: 试题详情
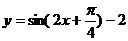 ,则原函数的解析式为_______ ,则原函数的解析式为_______
试题详情
试题详情
试题详情
试题详情
§5.4 向量的应用 〖复习要求〗理解向量的几何、代数、三角及物理方面的应用,能将当前问题转化为可用向量解决的问题,培养学生的创新精神和应用能力。 〖双基回顾〗 试题详情
试题详情
试题详情
试题详情
4.设A(x1,x2)、B(x2,y2),则SㄓAOB= ; ; 试题详情
试题详情
(1)若a=(x1,y1),b=(x2,y2),则a b=x1x2+y1y2; b=x1x2+y1y2;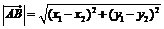 ; ; 试题详情
(2)若a=(x,y),则a2=a a=x2+y2, a=x2+y2,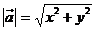 ; ; 试题详情
一、知识点训练: 1、若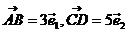 ,且 ,且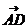 与 与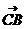 模相等,则四边形ABCD是_____ 模相等,则四边形ABCD是_____ A 平行四边形 B 梯形 C 等腰梯形 D 菱形 试题详情
试题详情
A 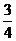 B B 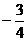 C 3
D -3 C 3
D -3 试题详情
3、1┧的重物在两根细绳的支持下处于平衡状态,如图:已知两根细绳与水平分别成30°,60°角,则两根细绳受到的拉力为______ 试题详情
4、某人以时速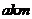 向东行走,此时正刮着时速 向东行走,此时正刮着时速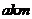 的南风,那么此人感到的风向为_____风速为___ 的南风,那么此人感到的风向为_____风速为___ 试题详情
二、典型例题分析: 1、空中有一气球,在它的正西方A点,测得它的仰角为45°,同时在它的南偏东45°的B点,测得它的仰角为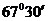 ,A、B两点间的距离为266米,这两点均离地1米,问当测量时,此气球离地多少米? ,A、B两点间的距离为266米,这两点均离地1米,问当测量时,此气球离地多少米? 试题详情
2、如图,用两根绳子把重10┧的物体W吊在水平杆子AB上,∠ACW=150°, ∠BCW=120°,求A和B处所受力的大小(忽略绳子重量) 试题详情
试题详情
试题详情
(2)要使船到达对岸所用的时间最少,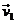 与 与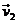 的夹角应为多少? 的夹角应为多少? 试题详情
试题详情
试题详情
三、课堂练习: 1、已知:A(2,3),B(1,4)且 ,则 ,则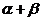 =______ =______ 试题详情
试题详情
3、已知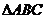 的BC边长的中点M,则 的BC边长的中点M,则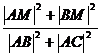 =_____ =_____ 试题详情
4、运用物理中矢量运算及向量坐标表示与运算,我们知道:(1)若两点等分单位圆时有相应关系式为: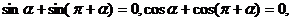 (2)四点等分单位圆时有相应关系式为: (2)四点等分单位圆时有相应关系式为: 试题详情
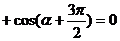 ,由此可以推知三等分单位圆时的相应关系式为_______ ,由此可以推知三等分单位圆时的相应关系式为_______
试题详情
试题详情
6、在一很大的湖岸边(可视湖岸为直线)停放着一只小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成15°角,速度为2.5km/h,同时岸边有一人,从同一地点开始追赶小船,已知他在岸上跑的速度为4km/h,在水中游的速度为2km/h. 问此人能否追上小船.若小船速度改变,则小船能被人追上的最大速度是多少? 平面向量单元测试题 试题详情
一、选择题: 1、 在四边形ABCD中,设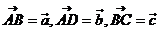 ,则 ,则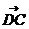 =_____ =_____ 试题详情
试题详情
2、 与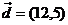 平行的单位向量为______ 平行的单位向量为______ 试题详情
试题详情
试题详情
试题详情
4、 非零向量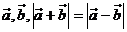 是 是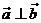 的_____ 的_____ A 充分而不必要条件 B
必要不充分条件 C
充要条件 D
既不充分也不必要条件 试题详情
试题详情
试题详情
试题详情
 ,则四边形ABCD的面积是____ ,则四边形ABCD的面积是____
试题详情
A 20 B
30 C 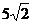 D 45 D 45 试题详情
7、设A(1,2),B(3,-1),C(3,4),则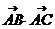 =____ =____ A 11 B 5 C -2 D 1 试题详情
试题详情
试题详情
9、在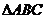 中,角A、B、C的对边为 中,角A、B、C的对边为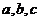 ,若 ,若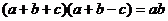 ,则角C等于_ ,则角C等于_ A 30° B
45° C 60° D 120° 试题详情
10、已知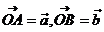 , , ,且恰有 ,且恰有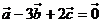 ,则A、B、C三点_____ ,则A、B、C三点_____ A 构成直角三角形 B
构成等腰三角形 C
共线 D
无法确定 试题详情
试题详情
12、已知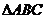 中,若 中,若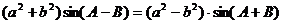 ,则 ,则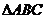 是_____ 是_____ A 等腰三角形 B
直角三角形 C
等腰直角三角形 D
等腰或直角三角形 试题详情
二、填空题: 13、已知:A(2,3),B(1,4)且 ,则 ,则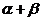 =______ =______ 试题详情
试题详情
15、已知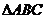 的BC边长的中点M,则 的BC边长的中点M,则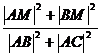 =_____ =_____ 试题详情
16、运用物理中矢量运算及向量坐标表示与运算,我们知道:(1)若两点等分单位圆时有相应关系式为: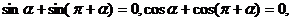 (2)四点等分单位圆时有相应关系式为: (2)四点等分单位圆时有相应关系式为: 试题详情
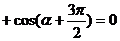 ,由此可以推知三等分单位圆时的相应关系式为_______ ,由此可以推知三等分单位圆时的相应关系式为_______
试题详情
三、解答题: 17、已知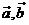 是两个不共线非零向量,若 是两个不共线非零向量,若 试题详情
(1)
求证:A、B、D三点共线;(2)确定实数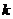 的值,使 的值,使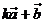 与 与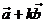 共线。 共线。 试题详情
18、设A、B为单位圆上两点,O为坐标原点,(A、O、B不共线)(1)求证: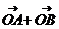 与 与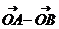 垂直;(2)当 垂直;(2)当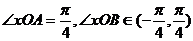 且 且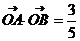 时,求 时,求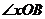 的正弦值。 的正弦值。 试题详情
19、海中有岛A,已知A岛四周8海里内有暗礁,今有一货轮由西向东航行,在B处望见A岛在北偏东75°,行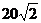 海里至C后见此岛在北偏东30°,如货轮不改变航向继续航行,问有无触礁危险? 海里至C后见此岛在北偏东30°,如货轮不改变航向继续航行,问有无触礁危险? 试题详情
试题详情
21、在一很大的湖岸边(可视湖岸为直线)停放着一只小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成15°角,速度为2.5km/h,同时岸边有一人,从同一地点开始追赶小船,已知他在岸上跑的速度为4km/h,在水中游的速度为2km/h. 问此人能否追上小船.若小船速度改变,则小船能被人追上的最大速度是多少? 试题详情
试题详情
| 
 .
. ),b=(
),b=( )则a
)则a b=(
b=( ).
). =
= 、
、 =
= 为邻边作平行四边形ABCD,则两条对角线的向量
为邻边作平行四边形ABCD,则两条对角线的向量 =
= +
+ ,
, =
= -
- ,
, =
= -
- 且有?
且有? ?-?
?-? ?≤?
?≤?

 ?≤?
?≤? ?+?
?+? ?.
?. +
+ =
= +
+ (交换律);
(交换律);  +(
+( +c)=(
+c)=( +
+  )+c
(结合律);
)+c
(结合律); +0=
+0=
 +(-
+(- )=0.
)=0. 与向量
与向量 的积是一个向量。
的积是一个向量。
 ?=?
?=? ???
??? ?;
?; >0时,
>0时,
 与
与 的方向相同;当
的方向相同;当 <0时,
<0时,
 与
与 的方向相反;当
的方向相反;当 =0时,
=0时,
 =0.
=0.  =(
=( ),则
),则 ?
? =(
=( ).
). 共线的充要条件是有且仅有一个实数
共线的充要条件是有且仅有一个实数 ,使得b=
,使得b=
 .
. =(
=( ),b=(
),b=( )则
)则 ∥b
∥b .
. ,有且只有一对实数
,有且只有一对实数 ,
, ,使得
,使得 =
= e1+
e1+  e2.
e2.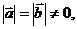 且
且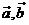 不共线时,
不共线时,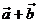 与
与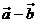 的关系是______
的关系是______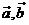 ,使得
,使得 ,那么
,那么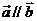 ;(2)若两非零向量
;(2)若两非零向量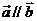 ,则
,则 ;(3)若
;(3)若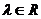 ,则
,则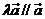 ;(4)若
;(4)若 ,则
,则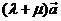 与
与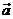 共线。其中正确命题的个数是_____
共线。其中正确命题的个数是_____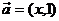 与
与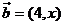 共线且方向相同,则
共线且方向相同,则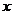 =_______
=_______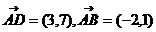 ,则
,则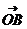 =________
=________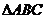 的重心,求证:
的重心,求证: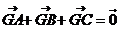
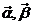 满足
满足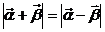 ,求
,求 与
与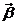 所成角的大小。
所成角的大小。 ,且
,且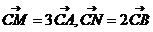 ,求M,N的坐标和
,求M,N的坐标和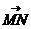
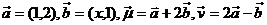 且
且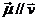 ,求
,求