
题目列表(包括答案和解析)
16.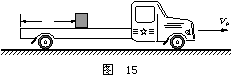 (16分)如图 15 所示,一平板车以某一速度 vo = 5
m/s 匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为
l =
(16分)如图 15 所示,一平板车以某一速度 vo = 5
m/s 匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为
l =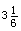 m ,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做
a1 = 3
m/s2 的匀减速直线运动。已知货箱与平板车之间的摩擦因数为 μ = 0.2 ,
m ,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做
a1 = 3
m/s2 的匀减速直线运动。已知货箱与平板车之间的摩擦因数为 μ = 0.2 ,
g = 10 m/s2 。求:
(1) 通过计算,判断货箱能否从车后端掉下来
(2) 如果货箱不能掉下,则最终停止时离车后端的距离 d 是多少
(3) 如果货箱不能掉下,最后都停止运动,平板车再从静止开始以 a2 = 4 m/s2 的加速度匀加速直线运动,经过 3 秒货箱距离车后端多远?已知平板车后端离地面高 1.25 m,货箱落地后不动
分析与解答: (1) 货箱放到车上后,先做匀加速运动,设经过时间 t 和车达到相同速度,此时货箱和车的位移分别为 x1 、x2
对货箱: μmg = ma1 a1t = vo – at x1 = vot - 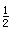 a1t 2
a1t 2
对平板车: x2 = vo t - 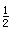 at 2
at 2
此时,货箱相对车向后移动了 △x = x2 – x1 = 2.5 m < l =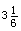 m ,
m ,
故货箱不会从车后端掉下来。
(2) 由于货箱的最大加速度 a1 = μg = 2 m/s2 < a ,所以二者达到相同速度后,分别以不同的加速度匀减速运动到停止,此时相同速度为 v = a1t = 2 m/s
对货箱: s1 = v2/2 a1 = 1 m 对平板车: s2 = v2/2a = 2/3 m
故货箱到车尾的距离 d1 = l - △x + s1 - s2 = 1 m
(3) 设经过时间
t1 货箱和车分离,由位移关系得:
d1 = 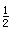 a2t12 -
a2t12 - 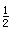 a1t12 解得 t1 = 1 s
a1t12 解得 t1 = 1 s
分离时货箱速度 v1 = a1t1 = 2 m/s ,货箱做平抛运动,经过时间 t2 落地,
∴ h = 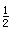 gt22 ,得
t2 = 0.5 s
gt22 ,得
t2 = 0.5 s
则在平板车启动的 t3 = 3 s 内,货箱的水平位移 x1’ = 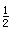 a1t12 + v1 t2 = 2 m
a1t12 + v1 t2 = 2 m
平板车的位移为: x2’ = 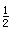 a2t32 = 18 m
a2t32 = 18 m
故货箱离平板车后端的距离: d2 = x2’ - x1’ - d1 = 15 m
15.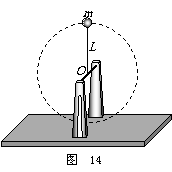 (9分)如图 14 所示,质量为 M 的支座上有一水平细轴。轴上套有
(9分)如图 14 所示,质量为 M 的支座上有一水平细轴。轴上套有
一长为 L 的细绳,绳的另一端栓一质量为 m 的小球,让球在竖直面内做均速圆
周运动,当小球运动到最高点时,支座恰好离开地面,则此时小球的线速度是多少?
分析与解答:对支座M,由牛顿运动定律,有: T - Mg = 0 ------ ①
对小球m,由牛顿第二定律,有: T + mg = m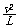 ---
②
---
②
联立 ①② 式可解得:v
= 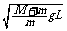
14. (8分)如图 12 所示,光滑斜面体的质量为M ,斜角为θ 。放置在光滑水平
(8分)如图 12 所示,光滑斜面体的质量为M ,斜角为θ 。放置在光滑水平
面上,要使质量为m 的物体能静止在光滑斜面体上,应对光滑斜面体施以多大的水平外
力F ?此时m 与 M 之间的相互作用力 N 为多大?
分析与解答:根据题意,则m与M所组成的系统在光滑水平面上有相同
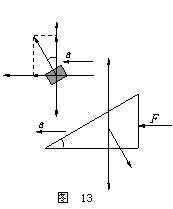 的加速度a,由受力分析图和牛顿第二定律,有: F = (M + m)a
的加速度a,由受力分析图和牛顿第二定律,有: F = (M + m)a
要求 m 与 M 之间的相互作用力 N ,先将 m 从系统中隔离出来,并对m
进行正确的受力分析如图 13 所示,建立如图所示的直角坐标,将 m 与 M 之间
的相互作用力进行正交分解,m在y方向为平衡态,在x方向为加速态。即其 x
方向的动力学方程和 y 方向的平衡方程分别为:
x: Ny - mg = 0 即 Ncosθ - mg = 0 ∴ N = mg/cosθ
y: Nx = ma 即 N sinθ = ma ∴ a = gtanθ
联立上述方程,解得 F = (M + m)gtanθ
13.(9分) 有一辆质量为 800 kg的小汽车驶上圆弧半径为 50 m的拱桥(地球半径R = 6400 km, g = 10 m/s2) 。求:
(1) 汽车到达桥顶时速度为 5 m/s,汽车对桥的压力是多大
(2) 汽车以多大速度经过桥顶时恰好对桥没有压力而腾空
(3) 如果拱桥的半径增大到与地球半径 R 一样,汽车要在桥面上腾空,速度要多大
分析与解答:(1) 当车在桥顶时, mg - FN = m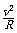 可解得 FN = 7600 N
可解得 FN = 7600 N
(2) 当车对桥顶的压力 FN = 0 时, 可解得 v = 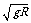 =
= 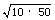 = 22.4 m/s
= 22.4 m/s
(3) 当桥的半径变为地球的半径时,可解得v’ =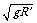 =
=
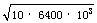 = 8000 m/s = 8 km/s
= 8000 m/s = 8 km/s
12. (12分)利用实验探究“当合外力大小一定时,物体
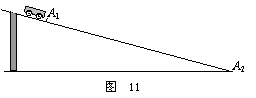 运动的加速度大小与其质量成反比”。给定的器材有:倾角可以
运动的加速度大小与其质量成反比”。给定的器材有:倾角可以
调节的长斜面(如图 11 所示).小车 、计时器 、米尺 、天平
(含砝码) 、钩码等 。在实验过程中不考虑摩擦,重力加速度
为 g ,请结合下列实验步骤回答相关问题。
(1) 用天平测出小车的质量为 mo
(2) 让小车自斜面上一固定点 A1 从静止开始下滑到斜面底端 A2 ,用计时器记下所用的时间为 to
(3) 用米尺测出 A1 与 A2 之间的距离 s ;则小车的加速度大小为 a = 2s/to2
(4) 用米尺测出 A1 相对于 A2 的竖直高度差 ho ,则小车所受的合外力大小为 F = mogho/s
(5) 在小车中加钩码,用天平测出此时小车与钩码的总质量 m ,同时通过改变斜面的倾角来改变固定点 A1 相对于 A2的竖直高度差 h ,测出小车从 A1 由静止开始下滑到斜面底端 A2 所需的时间 t ;问:质量不相等的前后两次应怎样操作才能使小车所受合外力大小一定?答: (mh = 定值) 。
(6) 多次改变小车与钩码的总质量进行实验,测出各次对应的 m 、h 、t 的值,以 1/t 2 为纵坐标, 1/m 为横坐标建立坐标系,根据各组数据在坐标系中描点,如果这些点在一条过原点的直线上,则可间接说明 当合外力大小一定时,物体运动的加速度大小与其质量成反比_ 。
11.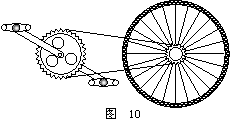 (6分) 如图 10 所示是自行车传动装置的示意图,若脚蹬匀速
(6分) 如图 10 所示是自行车传动装置的示意图,若脚蹬匀速
转一圈需要时间 T ,已数出大齿轮齿数为 48 ,小齿轮齿数为 16 ,要
知道在此情况下自行车前进的速度,还需要测量的物理量是 后轮半径 R
(填写该物理量的名称及符号) 。用这些量表示自行车前进速度的表达式
为 v = 6πR/T 。
10.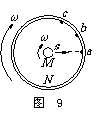 如图 9 所示,M 、N 是两个共轴圆筒的横截面,外筒半径为R,内筒半径比 R 小
如图 9 所示,M 、N 是两个共轴圆筒的横截面,外筒半径为R,内筒半径比 R 小
得多,可忽略不计。筒的两端是封闭的,两筒之间抽成真空。两筒以相同的角速度 ω 绕其
中心轴(垂直纸面)做匀速转动。设从 M 筒内部可以射出两种不同速度率 v1 和 v2 的微粒,
从 s 处射出时初速度的方向都是沿筒半径方向。微粒到达 N 筒后就附着在 N 筒上。如果 R 、
v1 、v2 都不变,取 ω 合适的值,则: (ABC)
A. 有可能使微粒落在 N 筒上的位置都在 a 处一条与 s 缝平行的窄条上
B. 有可能使微粒落在 N 筒上的位置都在某一处,如 b 处一条与 s 缝平行的窄条
C. 有可能使微粒落在 N 筒上的位置分别在某两处,如 b 处和 c 处与 s 缝平行的窄条上
D. 只要时间足够长, N 筒上将到处都落有微粒
9.设想人类开发月球,不断把月球上的矿藏搬运到地球上,假定经过长时间开采后,地球仍可看作是均匀的球体,月球仍沿开采前的圆周轨道运动,则与开采前相比(BD)
A.地球与月球间万有引力将变大 B.地球与月球间万有引力将变小
C.月球绕地球运动的周期将变长 D.月球绕地球运动周期将变短
分析与解答:地球与月球间的万有引力 F = G m月M地/R月地2 ,由数学知识可知,当m月 与 M地 相接近时,它们之间的万有引力较大,当它们的质量之差逐渐增大时(m月 与 M地 的乘积将减小),它们之间的万有引力值将减小,∴ A 选项错误,B 选项正确。假定经过长时间开采后,地球仍可看作是均匀的球体,月球仍沿开采前的圆周轨道运动(R不变 ),由开普勒第三行星定律 T 2/R 3 = k = 4π2/GM 可知,随着地球质量的逐步增加,将使月球绕地球运动周期将变短。∴ C 选项错误,D 选项正确。
8.一个物体从某一确定的高度以v0 的初速度水平抛出,已知
它落地时的速度为v1,那么它的运动时间是(D)
A.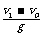 B.
B.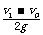 C.
C.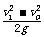 D.
D.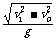
分析与解答:由于平抛运动是水平方向上的匀速直线运动与竖直方向上的自由落体运动的合运动,故任意时刻的速度是这两个分运动速度的合速度,当一个物体从某一确定的高度以v0 的初速度水平抛出,已知它落地时的速度为v1,故v1 是物体运动的末速度,由速度的分解法则可知,vy2 = v12 - vo2,∴ vy = 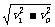 ,∴ 物体的运动时间
,∴ 物体的运动时间
t = vy /g =  /g 。 ∴ D 选项正确 。
/g 。 ∴ D 选项正确 。
7.一汽船过河,船速为v1,水流速度是 v2 ,v1 > v2 ,以下说法正确的是(BD)
A.船头指向上游与河岸成一定角度θ,cosθ = v2 /v1 时,航行的距离最短,所用的时间最短
B.船头指向上游与河岸成一定角度θ,cosθ = v2 /v1 时,航行的距离最短,所用的时间不是最短
C.船头指向垂直于河岸航行时,航行的距离最短,所用的时间最短
D.船头指向垂直于河岸航行时,航行的距离不是最短,所用时间最短
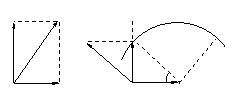 分析与解答:由图 8 所示可知,航行距离的最短值为河宽,
分析与解答:由图 8 所示可知,航行距离的最短值为河宽,
当合速度与河岸垂直时航行的距离最短,航行的距离最短时所用的
时间却不是最短的,只有以船速 v1 的值向垂直于河岸航行时所用时
间最短,综上所述,BD 选项正确。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com