2．为什么只有最大摆角很小的条件下，单摆才可看作简谐运动？

如图7－3－1所示，一般情况下，回复力F与单摆的位移x并不成正比，单摆的振动不是简谐运动，仅当摆角α很小时，因弧长AB与弦长AB(即位移x)差别很小，则sinα≈α此时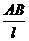≈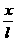所以F=mgsinα≈ mgα=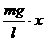也就是很小时，回复力才与位移成正比，单摆的振动可看成简谐运动．

例1．如图 7－3－2所示的光滑圆弧AB，它的圆心 O在槽的正上方，圆弧半径为R已知R>>AB·现同时在O处和A处自由释放两个很小的小球，前者自由下落，后者沿弧滚动，

则后者到达槽最低点　 图7－3－2

的时间是前者所用时间的多少倍？　　　 　　　　　　　　　　　　　　　

解析：对自由下落的小球：R=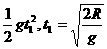,对沿槽滚下的小球t₂=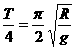,所以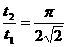,t₂=1.11t₁.

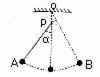
变式训练1：一个单摆的长为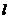，在其悬点O的正下方0.19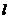处有一钉子P如图 7－3－3，现将摆球向左拉开到A，使摆线偏角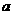<10°，放手使其摆动，求此单摆的振动周期　　 图7－3－3

解析：摆球作简谐运动的摆长有所变化，它的周期为两个不同单摆的半周期之和，即T=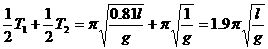　　 例2．如图 7－3－4所示，固定在天花板上等长的两根细线AO、BO长0.8m，与水平平面夹角都为53°，下端拴着质量m=0.2kg的小球(小球大小可忽略)，那么使小球在垂直纸面的竖直平面内摆动起来。求：

①如果摆角θ﹤10°，则小球的摆动周期。

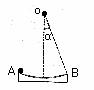②如果小球在摆动中到达最低点速度v=0.5m/s，则此时两细线受到的拉力各为解析：①此题首先设置了一个障碍，悬点未知，摆球的摆长是多少？此时双线摆的悬点为C点，所以等效摆长应为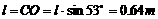，所以单摆周期为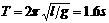； 图7－3－4

②通过受力分析可知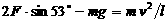 , 所以F≈1.3N 。

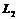
变式训练2:如在图 7－3－7中，三根等长的绳 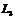共系住一密度均匀的小球m，球直径为d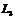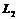，　 　与天花板的夹角θ﹤30°。　 　　　　图7－3－7

若摆球在纸面内作小角度的左右摆动，周期是多少？若摆球做垂直纸面的小角度摆动，则摆动圆弧的圆心在O处，故等效摆长为多少？周期是多少？

解析： 由题意可得若摆球在纸面内作小角度的左右摆动，周期为

，

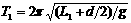若摆球做垂直纸面的小角度摆动，则摆长和周期分别为

，

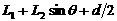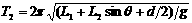
第四课时　 机械波

1．认为单摆振动的回复力就是单摆所受重力和线的拉力的合力，是否正确？为什么？

　　 (解答)不正确．单摆的振动是沿弧线经过某个中心位置的往复运动，既然是往复运动，必须有回复力的作用；又因为是曲线运动，还必须受到与速度有一角度的力．作用在单摆上的重力和拉力的共同作用将同时产生这两个效果．所以，将重力和拉力的合力理解为回复力是不正确的．

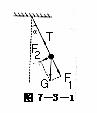　　 如图 7－3－1所示，将单摆的重力 G正交分解为F₁和 F₂，其中 T和F₁的共同作用提供摆球作圆弧运动的向心力，余下的F₁是回复力，所以，单摆的回复力F=Gsinα．

5、摆钟问题。单摆的一个重要应用就是利用单摆振动的等时性制成摆钟。在计算摆钟类的问题时，利用以下方法比较简单：在一定时间内，摆钟走过的格子数n与频率f成正比(n可以是分钟数，也可以是秒数、小时数……)，再由频率公式可以得到：

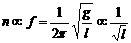
4、小球在光滑圆弧上的往复滚动，和单摆完全等同。只要摆角足够小，这个振动就是简谐运动。这时周期公式中的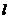应该是圆弧半径R和小球半径r的差。

3、当单摆的摆角很小时(小于10°)时，单摆的周期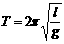，与摆球质量m、振幅A都无关。其中g为当地重力加速度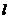，为摆长，表示从悬点到摆球质心的距离，要区分摆长和摆线长。

2、单摆振动的回复力是重力的切向分力，不能说成是重力和拉力的合力。在平衡位置振子所受回复力是零，但合力是向心力，指向悬点，不为零。

1、构造：用细线悬挂一小球，上端固定，如果悬挂小球的细线的伸缩和质量可以忽略，线长又比球的直径大得多，这样的装置叫单摆。

10.如图图7-2-2所示为同一地点的两单摆甲、乙的振动图象，下列说法中正确的是(　　 )

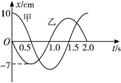图7-2-2

A.甲、乙两单摆的摆长相等　　　　　　　　

B.甲摆的振幅比乙摆大

C.甲摆的机械能比乙摆大　　　　　　　　　 D.在t=0.5 s时有正向最大加速度的是乙摆

答案：ABD

解析：振幅可从图上看出甲摆大，故B对.且两摆周期相等，则摆长相等.因质量关系不明确，无法比较机械能.t=0.5 s时乙摆球在负的最大位移处，故有正向最大加速度.所以正确选项选A、B、D.

第三课时　 单摆

3．图象形状的确定

　 　 选取的计时零点不同，图象的形状就不同，计时起点一旦确定，图象形状不变，仅随时间的增加逐渐延伸

判定某时刻质点的运动方向是看下一时刻质点的位置在哪里，其运动方向指向下一时刻的位置，即“前看后”。任一时刻的加速度方向都指向平衡位置．

例1 一个质点做简谐运动的图象如图7-2-1所示，下述正确的是(　　 )

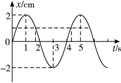图7-2-1

A.质点振动频率为4 Hz

B.在10 s内质点经过的路程是20 cm

C.在5 s末，质点速度为零，加速度最大

D.在t=1.5 s和t=4.5 s两时刻质点位移大小相等

答案：BCD

解析：由振动图象，可直接得到周期T=4 s，振动频率f=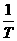=0.25 Hz，故A项错.

一个周期内，简谐运动的质点经过的路程是4A=8 cm，10 s为2.5个周期，质点经过的路程是20 cm，B项正确.

在5 s末，质点位移最大为2 cm，此时加速度最大，速度为零，C项是正确的.

在1.5 s和4.5 s两时刻，质点位移相等，故D项也正确.答案为B、C、D.

2．简谐运动图象不是质点的运动轨迹。

　 　做简谐运动的质点的轨迹是质点往复运动的那一段线段(弹簧振子)或那一段圆弧(单摆)，这种往复运动的位移与时刻的对应关系，用振动图象表示出来，并不是质点的运动轨迹。