波的干涉和衍射现象

1．波的叠加：两列波在空间相遇与分离时都保持其原来的特性(如f、A、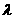、振动方向)沿原来方向传播，而不相干扰，在两列波重叠的区域里，任何一个质点同时参与两个振动，其振动位移等于这两列波分别引起的位移的矢量和，当两列波的振动方向在同一直线上时，这种位移的矢量和简化为代数和．

波动图象的周期性表现在时间的周期性和空间的周期性上。机械波在一个周期内不同时刻波形图象是不同的，但相隔时间为周期整数倍的图象的形状是安全相同的。这种周期性“必然导致波传播距离，时间和速度等有多个值与之对应，即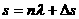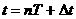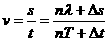，， (n=0,1,2…)抓住这几个关系就能正确求解，常表现为以下几个方面。(1)周期确定，传播距离不确定形成多解；(2)距离确定，周期不确定形成多解；(3)时间、距离都不确定形成多解，(4)传播方向不确定形成多解。

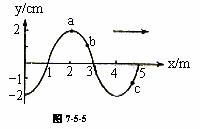例1. 已知某简谐横波波形图如图7-5-5所示，图中箭头表示波的传播方向，判断此时刻a、b、c三质点的振动方向。

解析：由波的传播方向和波形，可画出临近时刻的波形图如图2中虚线所示。b’、c’分别是b、c的临近时刻的位置，由此可得出：b质点向上运动，c质点向下运动，a质点处于波峰，运动速度为零，故无振动方向，所以选项AB对

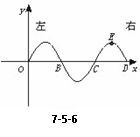
变式训练2.图7-5-6所示的是某横波的图象，由图可知

A、若波向右传播，则质点B正向右运动

B、若波向右传播，则质点C正向左运动

C、若波向左传播，则质点D正向下运动

D、若波向左传播，则质点B正向上运动

解析：同侧法：在波的图象的某一点，沿竖直方向画出一箭头表示质点振动方向，并设想在同一点沿水平方向画一箭头表示波的传播方向，那么这两箭头总是指向曲线的同侧，可称为“同侧法”。据此法过B点向左画一箭头表示波的传播方向，由“同侧”性规律，便知代表B点振动方向的箭头必然向下，故B点振动方向向下，同理D点振动方向向下，故选项C正确。)

例2．已知在t₁时刻简谐横波的波形如图7-5-7中实线所示；在时刻t₂该波的波形如图中虚线所示。t₂-t₁ = 0.02s求：⑴该波可能的传播速度。⑵若已知T< t₂-t₁<2T，且图中P质点在t₁时刻的瞬时速度方向向上，求可能的波速。⑶若0.01s<T<0.02s，且从t₁时刻起，图中Q质点比R质点先回到平衡位置，求可能的波速。

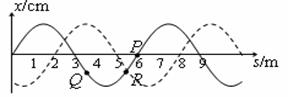
解析：⑴如果这列简谐横波是向右传播的，在t₂-t₁内波形向右匀速传播了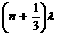，所以波速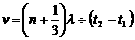=100(3n+1)m/s (n=0,1,2,…)；同理可得若该波是向左传播的，可能的波速v=100(3n+2)m/s　 (n=0,1,2,…)

　　 ⑵P质点速度向上，说明波向左传播，T< t2-t1 <2T，说明这段时间内波只可能是向左传播了5/3个波长，所以速度是唯一的：v=500m/s

⑶“Q比R先回到平衡位置”，说明波只能是向右传播的，而0.01s<T<0.02s，也就是T<0.02s<2T，所以这段时间内波只可能向右传播了4/3个波长，解也是唯一的：v=400m/s

变式训练2. 如图7-5-8所示，一列简谐波的波速为0.5m/s，实线为某时刻的波形图。经过Δt(Δt<T)后波形变为图中虚线所示，那么这段时间可能是(　　 )

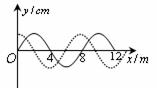图7-5-8

A、4s 　 B、8s 　　C、12s　 　 D、16s

解析：由题意可得选项AC正确

图7-5-7

第六课时　 波的特性

4.同侧法

在波的图形的某质点M上，沿波的传播方向画一箭头，再沿竖直方向向曲线的同侧画另一箭头，则该箭头即为质点振动方向，如图7-5-4所示.

3.上下坡法

沿波的传播方向看去，“上坡”处的质点向下振动。“下坡”处的质点向上振动。如图7-5-3所示，简称“上坡下，下坡上”

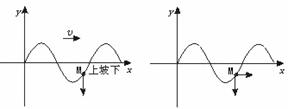图7-5-3　　　　　　 图7-5-4

2.微平移法：

所谓微移波形，即将波形沿波的传播方向平衡微小的一段距离得到经过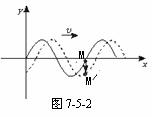微小一段时间后的波形图，据质点在新波形图中的对应位置，便可判断该质点的运动方向。如图 7－5－2所示，原波形图(实线)沿传播方向经微移后得到微小一段时间的波形图(虚线)，M点的对应位置在M′处，便知原时刻M向下运动。

1.质点带动法(特殊点法)：

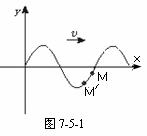
由波的形成传播原理可知，后振动的质点总是重复先振动质点的运动，若已知波的传播方向而判断质点振动方向时，可在波源一侧找与该点距离较近(小于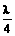)的前一质点，如果前一质点在该质点下方，则该质点将向下运动(力求重复前面质点的运动)，否则该质点向上运动。例如向右传的某列波，某时刻波的图象如图 7－5－1所示，试判断质点M的振动方向，可在波源一侧找出离M较近的前一质点′，M′在M下方，则该时刻M向下运动。

(1)平移法：利用运动公式Δx=v·Δt-v·nT= v·Δt-nλ，求出传播距离Δx，将波形图沿波传播方向平移Δx即得．

(2)特殊点法：先找出某些特殊点，确定其运动方向及经Δt这些点应到达的位置，最后再画正弦(或余弦)曲线即得．

注意：若求得是Δt前的波形，可将波形图逆波传播方向平移即可．若Δt＞T或Δx＞λ时，则可据波的重复性，先画出不足一周期的波形图，然后再补画完全．

3．波动图像的重复性(周期性)：相隔时间为周期整数倍的两个时刻的波形相同．

波动图像的双向性：不指定波的传播方向时，图像表示的波可能有两个相反的方向．

由于波的图像的重复性与双向性，使得有关波形问题常出现多解的情况，要引起足够的重视．

2．根据波的图像，知道波的传播方向，由波的传播原理可以判断某时刻各质点的运动方向．在某些情况下也能判断介质中任一质点开始振动时的振动方向(与介质中刚要开始振动的质点振动方向相同)。

1.振动图象和波的图象：振动图象和波的图象从图形上看好象没有什么区别，但实际上它们有本质的区别。

⑴物理意义不同：振动图象表示同一质点在不同时刻的位移；波的图象表示介质中的各个质点在同一时刻的位移。　　　　　　　　　　　　　　　

⑵图象的横坐标的单位不同：振动图象的横坐标表示时间；波的图象的横坐标表示距离。

⑶从振动图象上可以读出振幅和周期；从波的图象上可以读出振幅和波长。