
题目列表(包括答案和解析)
2、40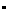 的余角为 ,补角为 。
的余角为 ,补角为 。
1、-2的相反数是 ,4的倒数为 ,16的平方根是 。
28、数学课上,老师出示图6和下面框中条件,
如图6,在直角坐标平面内,O为坐标为(1,0),点B在x轴上且在点A右侧,AB=OA,过点A和B作x轴的垂线,分别交二次函数y=x2的图像于点C和D,直线OC交BD于点M,直线CD交y轴于点H.记点C、D的横坐标分别为xCxD点H的纵坐标为yH.
同学发现两个结论: ①S△CMD:S梯形ABMC=2:3
②数值相等关系:xC·xD=-yH.
(1)请你验证结论①和结论②成立;
(2)请你研究:如果将上述框中的条件“A点坐标为(1,0)”改为“A点坐标为(t,0),(t>0)”,其他条件不变,结论①是否仍成立?(请说明理由)
(3)进一步研究:如果将上述框中的条件“A点坐标为(1,0)”改为“A点坐标为(t,0),(t>0) ”,又将条件“y=x2”改为“y=ax2(a>0)”,其他条件不变,那么xC、xD和yH有怎样的数值关系?(写出结果并说明理由)
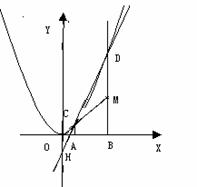
27、如图1,在矩形AB CD中,AB=20㎝,BC=4㎝,点P从A开始沿折线A-B-C-D以4㎝/s的速度移动,点Q从C开始沿CD边以1㎝/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动。设运动时间为t(s).
(1)t为何值时,四边形APQD为矩形?
(2)如图2,如果⊙P和⊙Q的半径都是2㎝,那么t为何值时,⊙P和⊙Q外切?

26、(本题满分9分)某工厂生产某种产品,每件产品的出厂价为1万元,其原材料成本价(含设备损耗等)为0.55万元,同时在生产过程中平均每年生产一件产品有1吨的废渣产生。为达到国家环保要求,需要对废渣进行脱硫、脱氮等处理,现有两种方案可供选择:
方案一 由工厂对废渣直接进行处理,每处理1吨废渣所用的原料费为0.05万元,并且每月设备维护及损耗费为20万元。
方案二 工厂将废渣集中到废渣处理厂统一处理,每处理1吨废渣需付0.1万元的处理费。
问:(1)设工厂每月生产x件产品,每月利润为y万元,分别求出方案一和方案二处理废渣时,y与x之间的函数关系式。(利润=总收入-总支出)
(2)若你作为工厂负责人,如何根据月生产量选择处理方案,既可达到环保要求又最合算。
25、如图2所示,△AOB为正三角形,点B坐标为(2,0),过点C(-2,0)作直线l交AO于点D,交AB于点E,且使△ADE和△DCO的面积相等,求直线l的函数解折式。

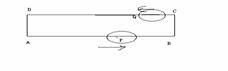
24、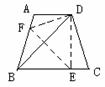 如图, 等腰梯形ABCD中,AD∥BC,∠DBC=45°。翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8,
如图, 等腰梯形ABCD中,AD∥BC,∠DBC=45°。翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8,
求:(1)BE的长;
(2)∠CDE的正切值。
23、某地举办乒乓球比赛的费用y元,包括两部分:一部分是租用比赛场地等固定不变的费用b(元),另一部分与参加比赛的人数x(人)成正比例。当x=20时,y=1600,当x=30时,y=2000。
(1)求y与x之间的函数关系式;
(2)如果有50名运动员参加比赛,且全部费用由运动员分摊,那么第每名运动员需要支付多少元?
22.先化简,在计算: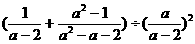 ,其中a=3
,其中a=3
20、观察下列各等式:
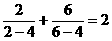
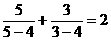
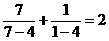
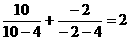
依照以上各式成立的规律,在括号中填人适当的数,使等式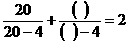
三:解答题(共82分)21.计算: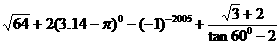
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com