
题目列表(包括答案和解析)
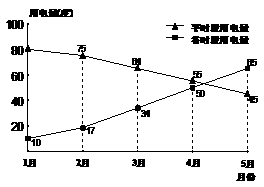
10、小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日6:00)分别计费,平时段每度电价与谷时段每度电价是不同的。小明将家里2006年1月至5月的平时段和谷时段的用电量分别用折线图表示(如下图),同时将前4个月的用电量和相应电费制成表格(如下表)
根据上述信息,解答下列问题:
(1) 平时段每度电 元,谷时段每度电 元
(2)计算5月份的用电量和相应电费,将所得结果填入表中;
(3)小明家这5个月的月平均用电量为 度;
(4)已知小明家7月份用电量为500度,相应电费为243元,请计算出7月份小明家平时段用电量和谷时段用电量.
|
|
月用电量(度) |
电费(元) |
|
1月 |
90 |
51.80 |
|
2月 |
92 |
50.85 |
|
3月 |
98 |
49.24 |
|
4月 |
105 |
48.55 |
|
5月 |
110 |
46.95 |
解:(1)平时段每度电0.61元,谷时段每度电0.3元
(2)如右表 (3)99
(4)设7月份小明家平时段用电x度,则谷时段用电(500-x)度,由题意,得:
 解得:x = 300 ∴500 – x= 500-300= 200
解得:x = 300 ∴500 – x= 500-300= 200
答:7月份小明家平时段用电300度,谷时段用电200度。
9、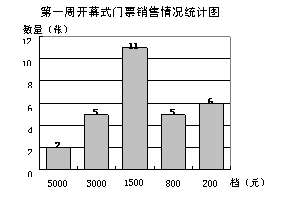 北京奥组委将分三个阶段向境内公众销售门票.2007年4月至9月为第一阶段,其核心销售政策是“公开认购、抽签确认”.4月15日至6月30日为申购期, 公众可以通过登录北京奥运会官方票务网站或提交纸质订单预订门票. 7至8月票务系统将对全部有效门票预订单进行统计并对申购数量大于售票数量的场次采用电脑抽签系统进行门票分配,在抽签系统中特别设计了一个程序,假设某人订购某档的门票没有被抽中,计算机系统会自动把他的订单降至下一个价格档再次参与抽签,直至最低档.开幕式门票分为A、B、C、D、E五个档次,票价分别为人民币5000元、3000元、1500元、800元和200元.已知境内可售开幕式门票有A档2000张、B档4000张、C档8000张、D档10000张、E档16000张. 假设所有境内可售开幕式门票均由100个门票代售网点代售.某网点第一周内开幕式门票的销售情况如图.
北京奥组委将分三个阶段向境内公众销售门票.2007年4月至9月为第一阶段,其核心销售政策是“公开认购、抽签确认”.4月15日至6月30日为申购期, 公众可以通过登录北京奥运会官方票务网站或提交纸质订单预订门票. 7至8月票务系统将对全部有效门票预订单进行统计并对申购数量大于售票数量的场次采用电脑抽签系统进行门票分配,在抽签系统中特别设计了一个程序,假设某人订购某档的门票没有被抽中,计算机系统会自动把他的订单降至下一个价格档再次参与抽签,直至最低档.开幕式门票分为A、B、C、D、E五个档次,票价分别为人民币5000元、3000元、1500元、800元和200元.已知境内可售开幕式门票有A档2000张、B档4000张、C档8000张、D档10000张、E档16000张. 假设所有境内可售开幕式门票均由100个门票代售网点代售.某网点第一周内开幕式门票的销售情况如图.
(1)第一周售出的门票票价的众数和中位数各是多少元?
由此能反映什么问题?
(2)假设每周所有网点售票情况大致相同.张老师申购
了1张A档门票,试问张老师是否需通过电脑抽签
才能分配到A档门票?若需要,他分配到A档门票的
概率大约是多少?(精确到1%)
(3)在⑵的假设下,王老师打算下周申购1张B档门票,
他分配到B档门票的可能性有多大?
(4)你认为⑵、⑶的估计是否合理?为什么?
解:(1)众数是1500元, (无单位不扣分)中位数是1500元. (无单位不扣分)
由此能反映公众对中等票价 (1500元) C档的门票较为青睐;
(2)张老师需通过电脑抽签才能分配到A档门票, P(张老师分配到A档门票)=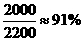 ;
;
(3)P(王老师分配到B档门票)=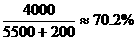 ;
;
[注]若按P(王老师分配到B档门票)=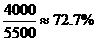 计算扣2分.
计算扣2分.
(4)⑵、⑶的估计不太合理.选取某一个网点第一周内开幕式门票的销售情况,无论从抽查对象的数量还是从抽查的时间来看,这一样本缺乏代表性,所以不能用这个样本的数据来估计100个网点11周的售票情况.
8、某公司经营甲、乙两种商品,甲种商品每件进价为12万元,售价为14.5万元;乙种商品每件进价为8万元,售价为10万元,且它们的进价和售价始终不变。现准备购进甲、乙两种商品共20件,所用进价成本 高于180万元,但不高于190万元。
高于180万元,但不高于190万元。
(1)若设购进甲商品为 件,请补全下表(填在横线上):
件,请补全下表(填在横线上):
|
商品 |
件数 |
进价成本(万元) |
利润(万元) |
|
甲 |
 |
 |
______ |
|
乙 |
___ |
______ |
______ |
|
合计 |
20 |
 |
 |
(2)请根据题意,列出 关于
关于 的关系式:___________;
的关系式:___________;
(3)根据(2),试确定该公司有哪几种进货方案?设两种商品全部销出后获得的利润为 万元,问哪种方案可获得最大的利润?并求出
万元,问哪种方案可获得最大的利润?并求出 的最大值。
的最大值。
解:(1)乙的件数: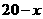 ,进价:
,进价: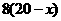 ;利润:甲为
;利润:甲为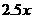 ;乙为
;乙为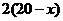 ;
;
(2)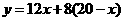
(3)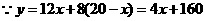 ,由题意:
,由题意: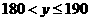
所以: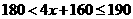 解得:
解得: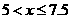
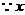 为整数,
为整数,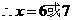 此时
此时 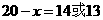
又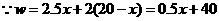 ,
, 随
随 的增大而增大 所以,当
的增大而增大 所以,当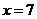 时,
时,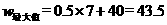 (万元)
(万元)
答:该公司有两种进货方案:方案一:甲商品6件,乙商品14件;方案二:甲商品7件,乙商品13件;
方案二可使得两种商品全部售出后能获得最大的利润为43.5万元。
7、姚明是我国著名的篮球运动员,他在2005-2006赛季NBA常规赛中表现非常优异.下面是他在这个赛季中,分期与“超音速队”和“快船队”各四场比赛中的技术统计.
(1)请分别计算姚明在对阵“超音速”和“快船”两队的各四场比赛中,平均每场得多少分?
(2)请你从得分的角度分析,姚明在与“超音速”和“快船”的比赛中,对阵哪一个队的发挥更稳定?
(3)如果规定“综合得分”为:平均每场得分×l+平均每场篮板×1.5十平均每场失误×(-1.5),且综合得分越高表现越好,那么请你利用这种评价方法,来比较姚明在分别与“超音速”和“快船”的各四场比赛中,对阵哪一个队表现更好?
解:⑴(22+29+24+26)÷4=25.25分 (25+29+17+22)÷4=23.25分
答: 姚明在对阵“超音速”的四场比赛中平均每场得25.25分,姚明在对阵“快船”的四场比赛中平均每场得23.25分
⑵超音速S2=(222+292+242+262)÷4-25.252=6.7
快船S2=(252+292+172+222)÷4-23.252=19.2
答:姚明在对阵“超音速”时发挥更稳定
⑶、超音速时综合得分25.25×1+11×1.5+2.75×(-1.5)=37.625
快船时综合得分23.25×1+12.75×1.5+2×(-1.5)= 39.375
答:姚明在对阵“快船”时表现更好
6、今年4月2日前,要求高收入的个人申报缴纳个人所得税.个人所得税实行累进税率,计算办法是用全月应纳税所得额分为几个级别,分别乘以累进税率,几个级别税额的总和就是该月应纳个人所得税额。全月应纳税所得额是用全月收入总额减去免税额(税法规定为800元)个人所得税的税率分为9个级数,下表列举了前5个级数:
|
级别 |
1级(500元之内的部分) |
2级(500元到2000元之间的部分) |
3级(2000元到5000元之间的部分) |
4级 |
5级(20000元到40000元之间的部分) |
|
税额 |
500×5%=25 |
1500×10%=150 |
3000×15%=450 |
15000×20%=3000 |
|
(1)请将表中的4级表示的部分以及5级的税额补充完整;
(2) 张华月收入2700元,那么他应缴纳的个人所得税为: 500×5%+(2700-800-500)×10%=165元;
若王明的月收入为2400元,那么他应缴纳的个人所得税是多少元?
(3) 若一个人缴纳的月个人所得税为3500元,那么这个人的月收入是多少元?
解:(1) ①4级(5000元到20000元之间的部分);
②20000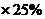 =50000
=50000
(2)500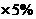 +(2400-800-500)
+(2400-800-500)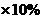 =25+110=135元
=25+110=135元
(3)设这个人的月收入为x元 得25+150+450+20%(x-5000-800)=3500 x=20175
答: 这个人的月收入为20175元 (若写出的答案为19375元的给2分)。
5、本商店积压了100件某种商品,为使这批货物尽快出售,该商店采取了如下销售方案,先将价格提高到原来的2.5倍,再作三次降价处理;第一次降价30%标出了“亏本价”,第二次降价30%,标出“破产价”,第三次又降价30%,标出“跳楼价”,三次降价处理销售情况如右表。
问:(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪一种方案更盈利,请通过计算加以说明
解:设原价为1
|
降价次数 |
一 |
二 |
三 |
|
销售件数 |
10 |
40 |
一抢而光 |
(1)亏本价=1×2.5(1-30%)=1.75
破产价=1.75(1-30%)=1.225
跳楼价=1.225(1-30%)=0.8575
跳楼价占原价的百分比为85.75%
(2)原价销售额:100×1=100
实际销售额:10×1.75+40×1.225+50×0.8575=109.375
∴按新销售方案销售更盈利。
4、某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,根据下图提供的信息,求一盒“福娃”玩具和一枚徽章的价格各是多少元?
 |
|||
|
解:设一盒“福娃”玩具和一枚徽章的价格分别为x元和y元.
依题意,得 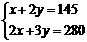 解这个方程组,得
解这个方程组,得 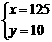
答:一盒“福娃”玩具和一枚徽章的价格分别为125元和10元.
3、随着温州经济的快速发展,温州已越来越吸引外来人员(新温州人)前来淘金创业,下列是市统计局公布的2004年,2006年新温州人相关的数据:
2004年,2006年温州新温州人人数统计图 2006年新温州人的温从业情况统计图


2006年新温州人在温的居住情况统计表
|
居住场所 |
租赁房屋暂住 |
单位内部宿舍 |
暂住当地居民家中 |
工地现场 |
旅店及其他场所 |
|
所占比例 |
56.57% |
32.53% |
3.55% |
2.14% |
5.21% |
请利用上述统计图表提供的信息回答下列问题:
(1)从2004年到2006年温州的“新温州人”增加了多少万人?
(2)2006年的“新温州人”中,经商的约为多少万人?
(3)请结合2006年“新温州人”在温州的居住情况统计表,谈谈你的看法或建议.
解:(1)276-235=41万 ∴2004年到2006年新温州人增加41万人
(2)3%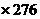 =8.28 ∴经商的约为8.28万人 若答案写成8万也不扣分。
=8.28 ∴经商的约为8.28万人 若答案写成8万也不扣分。
(3).答案不唯一.只要写出合理的答案就给分
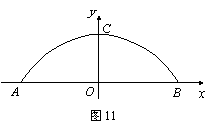
3、一座拱桥的轮廓是抛物线型(如图10所示),拱高6 m,跨度20 m,相邻两支柱间的距离均为5 m.
(1) 将抛物线放在所给的直角坐标系中(如图11所示),其表达式是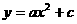 的形式.请根据所给的数据求出
的形式.请根据所给的数据求出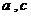 的值.
的值.
(2) 求支柱MN的长度.
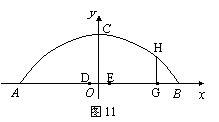
(3) 拱桥下地平面是双向行车道(正中间是一条宽2 m的隔离带),其中的一条行车道能否并排行驶宽2 m、高3 m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
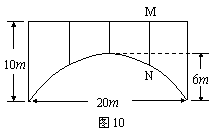
 解:(1)根据题目条件,A、B、C的坐标分别是(-10,0)、(0,6)、(10,0).
解:(1)根据题目条件,A、B、C的坐标分别是(-10,0)、(0,6)、(10,0).
将B、C的坐标代入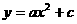 ,得
,得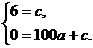 解得
解得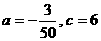 .
.
所以抛物线的表达式是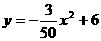 .
.
(2) 可设N(5,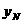 ),于是
),于是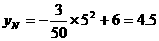 . 从而支柱MN的长度是
. 从而支柱MN的长度是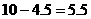 米.
米.
(3) 设DE是隔离带的宽,EG是三辆车的宽度和,则G点坐标是(7,0)(7=2÷2+2×3).
过G点作GH垂直AB交抛物线于H,则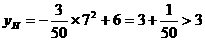 .
.
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.
2、为了迎接2008年北京奥运会的到来,某足球协会举办了一次足球联赛,其记分规则及奖励方案如下表:
|
|
胜一场 |
平一场 |
负一场 |
|
积 分 |
3 |
1 |
0 |
|
奖金(元/人) |
2000 |
1000 |
0 |
当比赛进行到14轮结束(每队均需比赛14场)时,甲队积分28分,设甲队胜x场,平y场.
⑴用x的代数式表示y;
⑵判断甲队胜、平、负各几场?并说明理由;
⑶若每赛一场,每名参赛队员均得出场费600元。设甲队中一名参赛队员所得的奖金与出场费的和为W(元),试求出W的最大值和最小值。
解:(1)∵3x+y=28, ∴y=-3x+28
(2) ∵ y=28-3x≥0 ∴x≤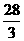
∵ X+y=28-2x≤14 ∴x≥7 ∴整数x =7或8或9
∴甲队胜,平,负的场数分别是:胜9场,平1场,负4场
或胜8场,平4场,负2场
或胜7场,平7场,负0场。
(3)W=2600x+1600(28-3x)+600(2x-14)=-1000x+36400
当x =7时W最大为29400元。当x =9时W最小为27400元。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com