
题目列表(包括答案和解析)
6、已知实数a, b满足等式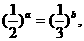 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有 ( )
A.1个 B.2个 C.3个 D.4个
 7 、
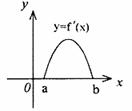
7 、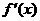 是
是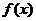 的导函数,
的导函数,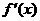 的图象如图所示,
的图象如图所示,
则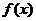 的图象只可能是(
)
的图象只可能是(
)

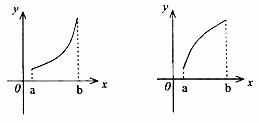
A B C D
5、设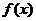 是可导函数,且
是可导函数,且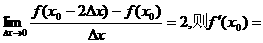 ( )
( )
A.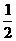 B.-1 C.0 D.-2
B.-1 C.0 D.-2
4. 函数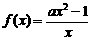 的单调递增区间为
的单调递增区间为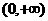 ,那么实数a的取值范围是 ( )
,那么实数a的取值范围是 ( )
A.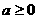 B.
B.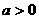 C.
C.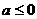 D.
D.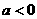
3.命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件;命题q:函数y=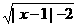 的定义域是(-∞,-1
的定义域是(-∞,-1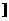 ∪[3,+∞
∪[3,+∞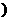 ,则( )
,则( )
(A)“p或q”为假 (B)“p且q”为真 (C) p真q假 (D) p假q真
2.奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则函数f(x-1)的图象为( )

1.设集合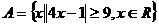 ,
, 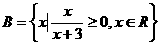 , 则A∩B=
, 则A∩B=
(A)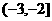 (B)
(B)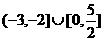 (C)
(C)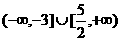 (D)
(D)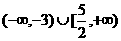
(15)(本小题12分)已知 |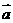 |=1,|
|=1,|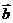 |=
|=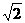 ,
,
(I)若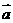 //
//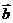 ,求
,求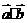 ; (II)若
; (II)若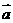 ,
,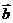 的夹角为135°,求 |
的夹角为135°,求 |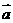 +
+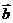 | .
| .
(16)(本小题12分) 袋中装有3个白球和4个黑球,现从袋中任取3个球,设ξ为所取出的3个球中白球的个数.
(I)求ξ的概率分布; (II)求Eξ.
(17)(本小题14分)
如图,已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为AA1、BB1的中点,求:
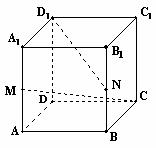 (I)CM与D1N所成角的余弦值;
(I)CM与D1N所成角的余弦值;
(II)异面直线CM与D1N的距离.
(18) (本小题14分)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM 上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米,
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
 (II)
若AN的长度不少于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最 小?并求出最小面积.
(II)
若AN的长度不少于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最 小?并求出最小面积.
(19)(本小题14分) 如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且 ,|BC|=2|AC|.
,|BC|=2|AC|.
(I)建立适当的坐标系,求椭圆方程;
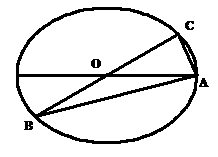 (II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,
(II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,
证明:存在实数λ,使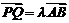 .
.
(20)(本小题14分) 已知数列{an}是首项为3,公比为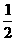 的等比数列,Sn是其前n项和.
的等比数列,Sn是其前n项和.
(Ⅰ)试用Sn表示Sn+1;
(Ⅱ)是否存在自然数c、k,使得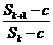 >3成立?证明你的论断.
>3成立?证明你的论断.
(11)由数字0、1、2、3、4组成无重复数字的5位数,其中奇数有 个.
(12)一个正四棱锥的底面边长为2,侧棱长为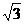 ,五个顶点都在同一个球面上,则此球的表面积为
.
,五个顶点都在同一个球面上,则此球的表面积为
.
(13)曲线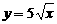 上与直线2x-y-4=0平行的切线的纵截距是 .
上与直线2x-y-4=0平行的切线的纵截距是 .
(14)设函数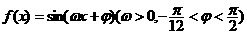 ,给出以下四个论断:
,给出以下四个论断:
①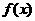 的周期为π; ②
的周期为π; ②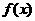 在区间(-
在区间(-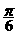 ,0)上是增函数;
,0)上是增函数;
③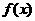 的图象关于点(
的图象关于点(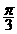 ,0)对称; ④
,0)对称; ④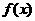 的图象关于直线
的图象关于直线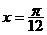 对称.
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
 (只需将命题的序号填在横线上).
(只需将命题的序号填在横线上).
(1)
不等式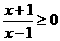 的解集是
的解集是
(A )
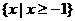 (B)
(B) 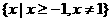
(C) 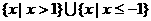 (D)
(D)
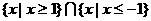
(2) 若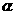 是第二象限的角,且
是第二象限的角,且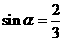 ,则
,则
(A)
 (B)
(B)
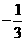 (C)
(C)
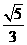 (D)
(D)
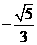
(3) 圆的一条直径的端点是A(2,0),B(2,-2),则圆的方程是
(A)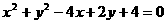 (B)
(B)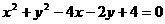
(C)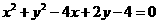 (D)
(D)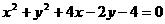
(4) 三棱锥D-ABC的三个侧面分别与底面全等,且AB=AC=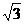 ,BC=2,则以BC为棱,以面BCD与BCA为面的二面角的大小为
,BC=2,则以BC为棱,以面BCD与BCA为面的二面角的大小为
(A) 300 (B) 450 (C)600 (D)900
(5) 下列各式中,对任何实数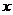 都成立的一个是
都成立的一个是
(A) 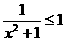 (B)
(B)
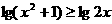 (C)
(C)
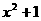
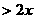 (D)
(D)
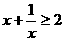
(6)
等差数列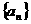 中,
中,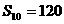 ,那么
,那么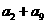 的值是
的值是
(A) 12 (B) 24 (C) 16 (D) 48
(7) 下列命题中,正确的是
(A)平行于同一平面的两条直线平行
(B)与同一平面成等角的两条直线平行
(C)与同一半平面成相等二面角的两个半平面平行
(D)若平行平面与同一平面相交,则交线平行
(8) 二项式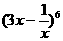 的展开式的常数项是
的展开式的常数项是
(A)20 (B)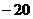 (C)540 (D)
(C)540 (D)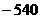
(9) 电灯泡使用时数在1000小时以上的概率为0.8,则3个灯泡在使用1000小时内恰好坏了一个的概率为
(A) 0.384
(B)  (C) 0.128
(D) 0.104
(C) 0.128
(D) 0.104
(10)
已知目标函数z=2x+y,且变量x、y满足下列条件: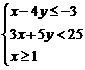 ,则
,则
(A) z最大值=12,z无最小值 (B) z最小值=3,z无最大值
(C)
z最大值=12,z最小值=3 (D) z最小值=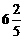 ,z无最大值
,z无最大值
22.(本小题满分13分)已知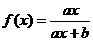 且不等式
且不等式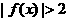 的解集为
的解集为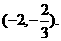
(1)求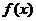 的解析式;
的解析式;
(2)设数列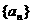 满足:
满足: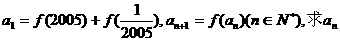 ;
;
(3)设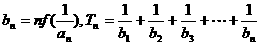 ,数列
,数列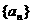 的前n项和为
的前n项和为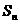 ,求证:
,求证:
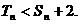
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com