
题目列表(包括答案和解析)
7、(2006吉林长春)某厂生产一种零件,每个成本为40元,销售单价为60元。该厂为了鼓励客户购买,决定当一次购买零件超过100个时,多购买一个,全部零件的销售单价均降低0.02元,但不能低于51元。
(1)当一次购买多少个零件时,销售单价恰为51元?
(2)设一次购买零件x个时,销售单价为y元,求y与x的函数关系式。
(3)当客户一次购买500个零件时,该厂获得的利润是多少?当客户一次购买1000个零碎件时,利润又是多少?(利润 = 售价-成本)
[解析]
(1)设当一次购买x个零件时,销售单价为51元,则
(x-100)×0.02 = 60-51,
解得 x = 550。
答:当一次购买550个零件时,销售单价为51元。
(2)当0<x≤100时, y = 60;
当100<x≤550时, y = 62-0.02x;
当x>550时, y = 51。
(3)当x = 500时,利润为
(62-0.02×500)×500-40×500 = 6000(元)。
当x = 1000时,利润为1000×(51-40)= 11000(元)。
答:当一次购买500个零件时,该厂获得利润为6000元;当一次购买1000个零件时,该厂获得利润11000元。
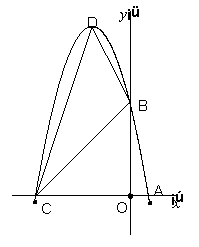
6、(2006山东烟台)如图,已知抛物线L1: y=x2-4的图像与x有交于A、C两点
(1)若抛物线l2与l1关于x轴对称,求l2的解析式;
(2)若点B是抛物线l1上的一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在l2上;
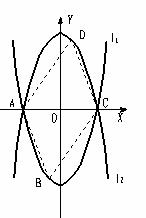 (3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
(3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
[解析] (1)设l2的解析式为y=a(x-h)2+k
∵l2与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),l1与l2关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4)
∴y=ax2+4
∴0=4a+4 得 a=-1
∴l2的解析式为y=-x2+4
(2)设B(x1 ,y1)
∵点B在l1上
∴B(x1 ,x12-4)
∵四边形ABCD是平行四边形,A、C关于O对称
∴B、D关于O对称
∴D(-x1 ,-x12+4).
将D(-x1 ,-x12+4)的坐标代入l2:y=-x2+4
∴左边=右边
∴点D在l2上.
(3)设平行四边形ABCD的面积为S,则
S=2*S△ABC =AC*|y1|=4|y1|
a.当点B在x轴上方时,y1>0
∴S=4y1 ,它是关于y1的正比例函数且S随y1的增大而增大,
∴S既无最大值也无最小值
b.当点B在x轴下方时,-4≤y1<0
∴S=-4y1 ,它是关于y1的正比例函数且S随y1的增大而减小,
∴当y1 =-4时,S由最大值16,但他没有最小值
此时B(0,-4)在y轴上,它的对称点D也在y轴上.
∴AC⊥BD
∴平行四边形ABCD是菱形
此时S最大=16.
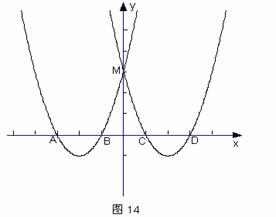
5、如图14,抛物线E: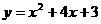 交x轴于A、B两点,
交x轴于A、B两点,
交y轴于M点。抛物线E关于y轴对称的抛物线F交x轴于
C、D两点。
⑴求F的解析式;
⑵在x轴上方的抛物线F或E上是否存在一点N,使以A、C
N、M为顶点的四边形是平行四边形。若存在,求点N坐标;
若不存在,请说明理由;
⑶若将抛物线E的解析式改为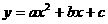 ,试探索问题⑵。
,试探索问题⑵。
[解析] 当y=0时,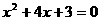 ,解得x1=-3,x2=-1,
,解得x1=-3,x2=-1,
∴A、B点坐标分别为(-3,0)、(-1,0)
当x=0时,y=3,∴M点坐标为(0,3),A、B、M三点关于y轴得对称点分别是D、C、M,∴D、C坐标为(3,0)、(1,0)
设F的解析式为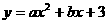
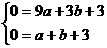
∴a=1,b=-4
∴F的解析式为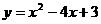
(2)存在。假设MN∥AC,∴N点的纵坐标为3。
若在抛物线F上,当y=3时,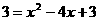 ,则x1=0,x2=4
,则x1=0,x2=4
∴N点坐标为(4,3),∴MN=4,
由(1)可求AC=4,∴MN=AC,∴四边形ACNM为平行四边形。
根据抛物线F和E关于y轴对称,故N点坐标为(4,3)或(-4,3)
(3) 存在。假设MN∥AC,∴N点的纵坐标为c。设y=0,∴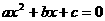
∴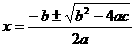 ,
,
∴A点坐标为(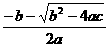 ,0),B点坐标为(
,0),B点坐标为(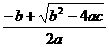 ,0)
,0)
∴C点坐标为(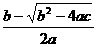 ,0),∴AC=
,0),∴AC=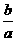
在抛物线E上,当y=c时,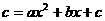 ,x1=0,x2=
,x1=0,x2=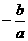
∴N点坐标为(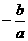 ,0)
,0)
NM=0-(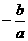 )=
)=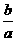 ,∴NM=AC,∴四边形ACMN为平行四边形。
,∴NM=AC,∴四边形ACMN为平行四边形。
根据抛物线F和E关于y轴对称,故N点坐标为(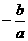 ,c)或(
,c)或(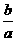 ,c)。
,c)。
4、(2006浙江嘉兴)某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为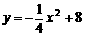 ,BC所在抛物线的解析式为
,BC所在抛物线的解析式为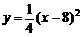 ,且已知
,且已知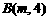 .
.
(1)设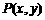 是山坡线AB上任意一点,用y表示x,并求点B的坐标;
是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一直铺到山脚,为什么?
 (3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,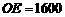 (米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为
(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为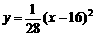 .试求索道的最大悬空高度.
.试求索道的最大悬空高度.
[解析] (1)∵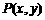 是山坡线AB上任意一点,
是山坡线AB上任意一点,
∴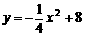 ,
,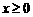 ,
,
∴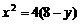 ,
,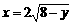
∵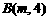 ,∴
,∴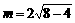 =4,∴
=4,∴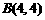
(2)在山坡线AB上,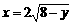 ,
,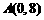
①令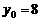 ,得
,得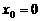 ;令
;令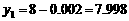 ,得
,得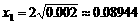
∴第一级台阶的长度为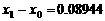 (百米)
(百米)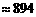 (厘米)
(厘米)
同理,令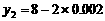 、
、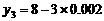 ,可得
,可得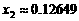 、
、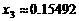
∴第二级台阶的长度为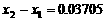 (百米)
(百米)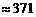 (厘米)
(厘米)
第三级台阶的长度为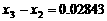 (百米)
(百米)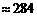 (厘米)
(厘米)
②取点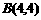 ,又取
,又取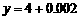 ,则
,则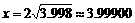
∵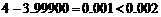
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性)
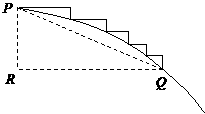 ②另解:连接任意一段台阶的两端点P、Q,如图
②另解:连接任意一段台阶的两端点P、Q,如图
∵这种台阶的长度不小于它的高度
∴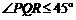
当其中有一级台阶的长大于它的高时,
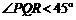
在题设图中,作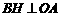 于H
于H
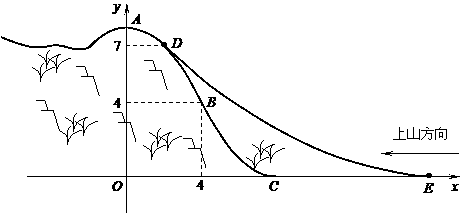 则
则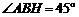 ,又第一级台阶的长大于它的高
,又第一级台阶的长大于它的高
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
(3)
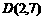 、
、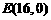 、
、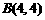 、
、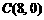
由图可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值
索道在BC上方时,悬空高度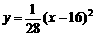
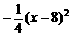
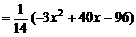
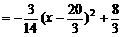
当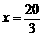 时,
时,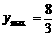
∴索道的最大悬空高度为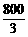 米.
米.
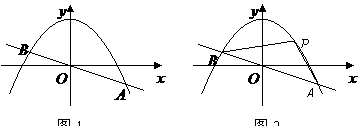
3、(2006北京海淀)已知抛物线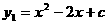 的部分图象如图1所示。
的部分图象如图1所示。
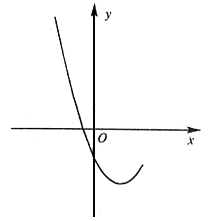
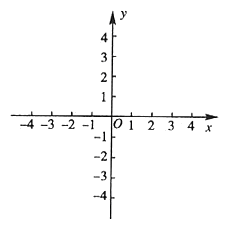
图1 图2
(1)求c的取值范围;
(2)若抛物线经过点(0,-1),试确定抛物线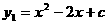 的解析式;
的解析式;
(3)若反比例函数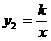 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较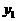 与
与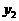 的大小。
的大小。
[解析] (1)根据图象可知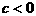
且抛物线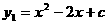 与x轴有两个交点
与x轴有两个交点
所以一元二次方程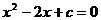 有两个不等的实数根。
有两个不等的实数根。
所以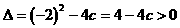 ,且
,且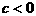
所以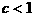
(2)因为抛物线经过点(0,-1)
把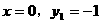 代入
代入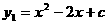
得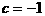
故所求抛物线的解析式为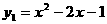
(3)因为反比例函数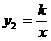 的图象经过抛物线
的图象经过抛物线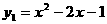 上的点(1,a)
上的点(1,a)
把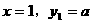 代入
代入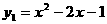 ,得
,得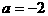
把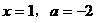 代入
代入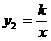 ,得
,得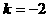
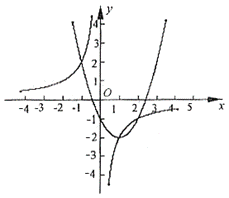 所以
所以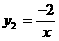
画出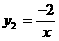 的图象如图所示。
的图象如图所示。
观察图象,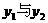 除交点(1,-2)外,还有两个交点大致为
除交点(1,-2)外,还有两个交点大致为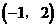 和
和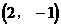
把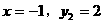 和
和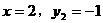 分别代入
分别代入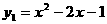 和
和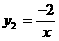 可知,
可知,
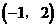 和
和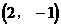 是
是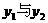 的两个交点
的两个交点
根据图象可知:当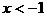 或
或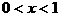 或
或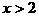 时,
时,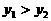
当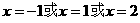 时,
时,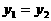
当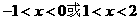 时,
时,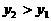
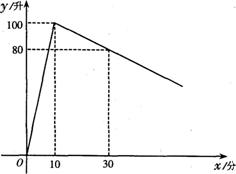
2、(2006黑龙江鸡西)某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程:加工过程中,当油箱中油量为10升时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复.已知机器需运行185分钟才能将这批工件加工完.下图是油箱中油量y(升)与机器运行时间x(分)之间的函数图象.根据图象回答下列问题:
 (1)求在第一个加工过程中,油箱中油量y(升)与机器运行时间x(分)之间的函数关系式(不必写出自变量x的取值范围);
(1)求在第一个加工过程中,油箱中油量y(升)与机器运行时间x(分)之间的函数关系式(不必写出自变量x的取值范围);
(2)机器运行多少分钟时,第一个加工过程停止?
(3)加工完这批工件,机器耗油多少升?
[解析] (1)设所求函数关系式为y=kx+b.
由图象可知过(10,100),(30,80)两点,
得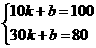
解得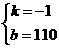
∴ y=-x+llO
(2)当y=10时,-x+110=10,x=100
机器运行100分钟时,第一个加工过程停止
(3)第一个加工过程停止后再加满油只需9分钟
加工完这批工件,机器耗油166升
1、(2006重庆)已知: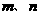 是方程
是方程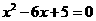 的两个实数根,且
的两个实数根,且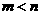 ,抛物线
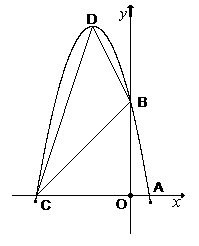
,抛物线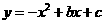 的图像经过点A(
的图像经过点A(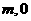 )、B(
)、B(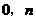 ).
).
(1) 求这个抛物线的解析式;
(2)  设(1)中抛物线与
设(1)中抛物线与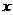 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线
轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线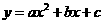
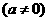 的顶点坐标为
的顶点坐标为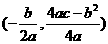 )
)
(3) P是线段OC上的一点,过点P作PH⊥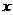 轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
[解析] (1)解方程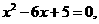 得
得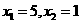
由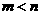 ,有
,有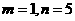
所以点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入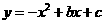 .
.
得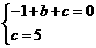 解这个方程组,得
解这个方程组,得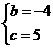
所以,抛物线的解析式为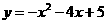
(2)由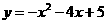 ,令
,令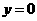 ,得
,得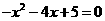
解这个方程,得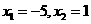
所以C点的坐标为(-5,0).由顶点坐标公式计算,得点D(-2,9).
过D作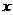 轴的垂线交
轴的垂线交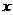 轴于M.
轴于M.
则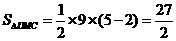
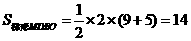 ,
,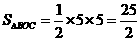
所以,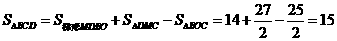 .
.
(3)设P点的坐标为(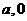 )
)
因为线段BC过B、C两点,所以BC所在的值线方程为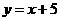 .
.
那么,PH与直线BC的交点坐标为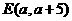 ,
,
PH与抛物线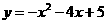 的交点坐标为
的交点坐标为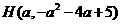 .
.
由题意,得①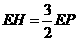 ,即
,即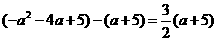
解这个方程,得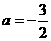 或
或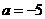 (舍去)
(舍去)
②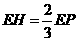 ,即
,即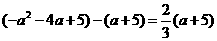
解这个方程,得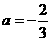 或
或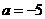 (舍去)
(舍去)
P点的坐标为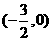 或
或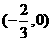 .
.
33.已知二次函数图象的顶点在原点 ,对称轴为
,对称轴为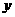 轴.一次函数
轴.一次函数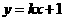 的图象与二次函数的图象交于
的图象与二次函数的图象交于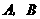 两点(
两点( 在
在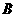 的左侧),且
的左侧),且 点坐标为
点坐标为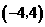 .平行于
.平行于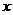 轴的直线
轴的直线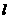 过
过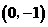 点.
点.
(1)求一次函数与二次函数的解析式;
(2)判断以线段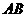 为直径的圆与直线
为直径的圆与直线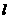 的位置关系,并给出证明;
的位置关系,并给出证明;
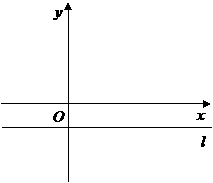 (3)把二次函数的图象向右平移
(3)把二次函数的图象向右平移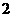 个单位,再向下平移
个单位,再向下平移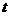 个单位
个单位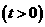 ,二次函数的图象与
,二次函数的图象与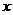 轴交于
轴交于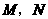 两点,一次函数图象交
两点,一次函数图象交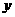 轴于
轴于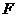 点.当
点.当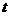 为何值时,过
为何值时,过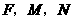 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?
解:(1)把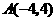 代入
代入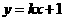 得
得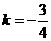 ,
,
 一次函数的解析式为
一次函数的解析式为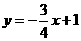 ;
;
 二次函数图象的顶点在原点,对称轴为
二次函数图象的顶点在原点,对称轴为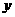 轴,
轴,
 设二次函数解析式为
设二次函数解析式为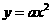 ,
,
把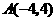 代入
代入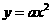 得
得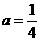 ,
,
 二次函数解析式为
二次函数解析式为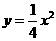 .
.
 (2)由
(2)由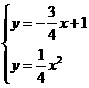
解得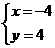 或
或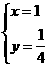 ,
,
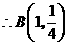 ,
,
过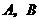 点分别作直线
点分别作直线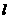 的垂线,垂足为
的垂线,垂足为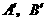 ,
,
则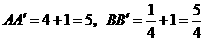 ,
,
 直角梯形
直角梯形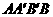 的中位线长为
的中位线长为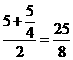 ,
,
过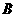 作
作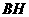 垂直于直线
垂直于直线 于点
于点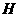 ,则
,则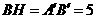 ,
,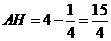 ,
,
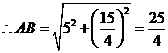 ,
,

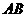 的长等于
的长等于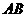 中点到直线
中点到直线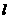 的距离的2倍,
的距离的2倍,
 以
以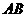 为直径的圆与直线
为直径的圆与直线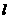 相切.
相切.
(3)平移后二次函数解析式为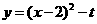 ,
,
令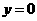 ,得
,得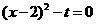 ,
,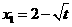 ,
,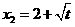 ,
,
 过
过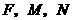 三点的圆的圆心一定在直线
三点的圆的圆心一定在直线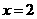 上,点
上,点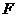 为定点,
为定点,
 要使圆面积最小,圆半径应等于点
要使圆面积最小,圆半径应等于点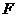 到直线
到直线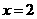 的距离,
的距离,
此时,半径为2,面积为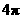 ,
,
设圆心为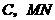 中点为
中点为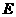 ,连
,连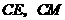 ,则
,则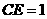 ,
,
在三角形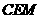 中,
中,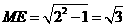 ,
,
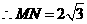 ,而
,而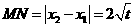 ,
,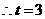 ,
,
 当
当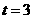 时,过
时,过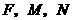 三点的圆面积最小,最小面积为
三点的圆面积最小,最小面积为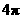 .
.
32.已知: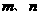 是方程
是方程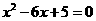 的两个实数根,且
的两个实数根,且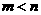 ,抛物线
,抛物线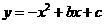 的图像经过点A(
的图像经过点A(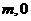 )、B(
)、B(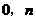 ).
).
(1) 求这个抛物线的解析式;
(2)
设(1)中抛物线与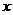 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线
轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线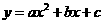
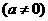 的顶点坐标为(
的顶点坐标为(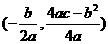 )
)
(3)  P是线段OC上的一点,过点P作PH⊥
P是线段OC上的一点,过点P作PH⊥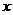 轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
解:(1)解方程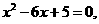 得
得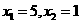
由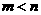 ,有
,有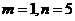
所以点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入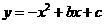 .
.
得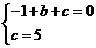 解这个方程组,得
解这个方程组,得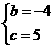
所以,抛物线的解析式为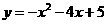
(2)由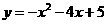 ,令
,令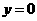 ,得
,得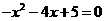
解这个方程,得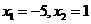
所以C点的坐标为(-5,0).由顶点坐标公式计算,得点D(-2,9).
过D作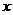 轴的垂线交
轴的垂线交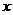 轴于M.
轴于M.
则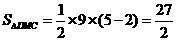
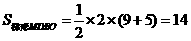 ,
,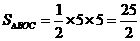
所以,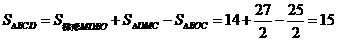 .
.
(3)设P点的坐标为(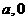 )
)
因为线段BC过B、C两点,所以BC所在的值线方程为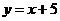 .
.
那么,PH与直线BC的交点坐标为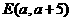 ,
,
PH与抛物线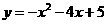 的交点坐标为
的交点坐标为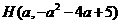 .
.
由题意,得①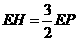 ,即
,即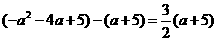
解这个方程,得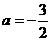 或
或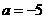 (舍去)
(舍去)
②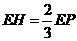 ,即
,即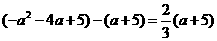
解这个方程,得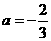 或
或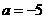 (舍去)
(舍去)
P点的坐标为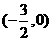 或
或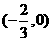 .
.
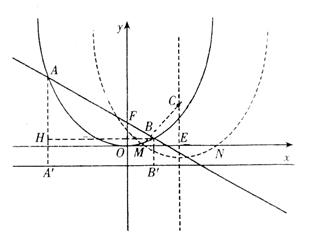
31.如图1,已知直线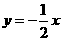 与抛物线
与抛物线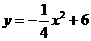 交于
交于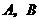 两点.
两点.
(1)求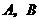 两点的坐标;
两点的坐标;
(2)求线段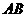 的垂直平分线的解析式;
的垂直平分线的解析式;
(3)如图2,取与线段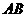 等长的一根橡皮筋,端点分别固定在
等长的一根橡皮筋,端点分别固定在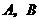 两处.用铅笔拉着这根橡皮筋使笔尖
两处.用铅笔拉着这根橡皮筋使笔尖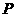 在直线
在直线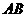 上方的抛物线上移动,动点
上方的抛物线上移动,动点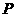 将与
将与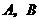 构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时
构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时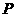 点的坐标;如果不存在,请简要说明理由.
点的坐标;如果不存在,请简要说明理由.
解:(1)解:依题意得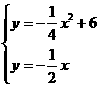 解之得
解之得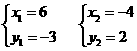
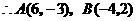
 (2)作
(2)作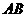 的垂直平分线交
的垂直平分线交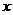 轴,
轴,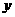 轴于
轴于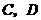 两点,交
两点,交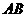 于
于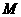 (如图1)
(如图1)
由(1)可知: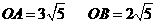
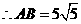
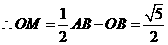
过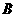 作
作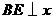 轴,
轴,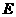 为垂足
为垂足
由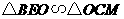 ,得:
,得: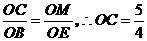 ,
,
同理: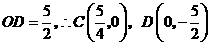
设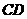 的解析式为
的解析式为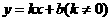
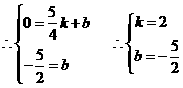
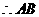 的垂直平分线的解析式为:
的垂直平分线的解析式为: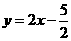 .
.
(3)若存在点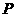 使
使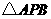 的面积最大,则点
的面积最大,则点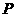 在与直线
在与直线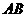 平行且和抛物线只有一个交点的直线
平行且和抛物线只有一个交点的直线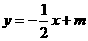 上,并设该直线与
上,并设该直线与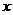 轴,
轴,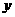 轴交于
轴交于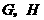 两点(如图2).
两点(如图2).
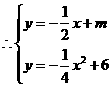
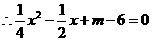
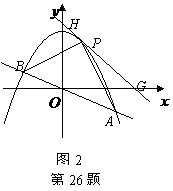
 抛物线与直线只有一个交点,
抛物线与直线只有一个交点,
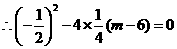 ,
,
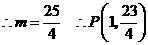
在直线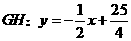 中,
中,
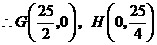
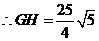
设 到
到 的距离为
的距离为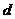 ,
,
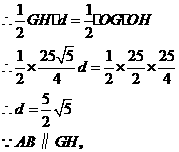
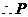 到
到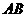 的距离等于
的距离等于 到
到 的距离
的距离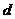 .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com