
题目列表(包括答案和解析)
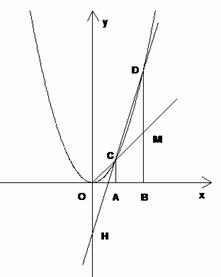
3、(2005年内江)教师提出:如图A(1,0),AB=OA,过点A、B作x轴的垂线交二次函数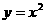 的图象于C、D两点,直线OC交BD于点M,直线CD交y轴于点H,记点C、D的横坐标分别为
的图象于C、D两点,直线OC交BD于点M,直线CD交y轴于点H,记点C、D的横坐标分别为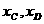 ,点H的纵坐标为
,点H的纵坐标为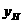 。
。
同学讨论发现:①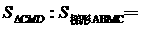 2 :3 ②
2 :3 ②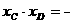
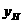
⑴请你验证①②结论成立;
⑵请你研究:如将上述条件“A(1,0)”改为“A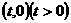 ”,其他条件不娈,结论①是否仍成立?
”,其他条件不娈,结论①是否仍成立?
⑶进一步研究:在⑵的条件下,又将条件“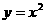 ”改为“
”改为“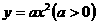 ,其他条件不娈,那么
,其他条件不娈,那么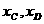 和
和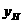 有怎样的数值关系?(写出结果并说明理由)
有怎样的数值关系?(写出结果并说明理由)
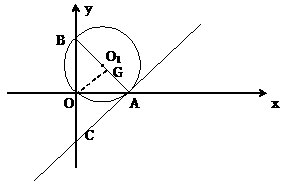
2、(北京丰台)在直角坐标系中,⊙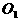 经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B。
经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B。
(1)如图,过点A作⊙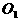 的切线与y轴交于点C,点O到直线AB的距离为
的切线与y轴交于点C,点O到直线AB的距离为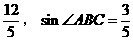 ,求直线AC的解析式;
,求直线AC的解析式;
(2)若⊙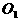 经过点M(2,2),设
经过点M(2,2),设 的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。
的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。
1、(包头)已知一次函数y1=x,二次函数y2=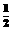 x2+
x2+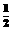 。
。
(1)根据表中给出的x的值,填写表中空白处的值;(2分)
|
x |
―3 |
―2 |
―1 |
0 |
1 |
2 |
3 |
|
y1=x |
―3 |
―2 |
―1 |
0 |
1 |
2 |
3 |
y2=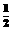 x2+ x2+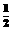 |
|
|
1 |
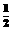 |
1 |
|
|
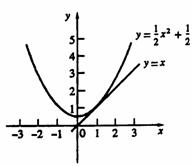 (2)观察上述表格中的数据,对于x的同一个值,判断yl和y2的大小关系。并证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1和y2的大小关系仍然成立;
(2)观察上述表格中的数据,对于x的同一个值,判断yl和y2的大小关系。并证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1和y2的大小关系仍然成立;
(3)若把y1=x换成与它平行的直线y=x+k(k为任意非零实数),请进一步探究:当k满足什么条件时,(2)中的结论仍然成立;当k满足什么条件时,(2)中的结论不能对任意的实数x都成立,并确定使(2)中的结论不成立的x的范围。
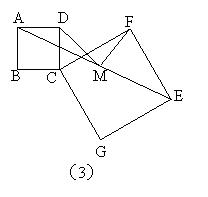
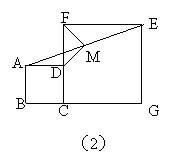
5、如图1,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M。
探究:线段MD、MF的关系,并加以证明。
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程之后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明。
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分。
① DM的延长线交CE于点N,且AD=NE;
② 将正方形CGEF绕点C逆时针旋转45°(如图2),
其他条件不变;③在②的条件下且CF=2AD。
附加题:将正方形CGEF绕点C旋转任意角度后(如图3),其他条件不变。探究:线段MD、MF的关系,并加以证明。
例2(连云港)如图,将一块直角三角形纸板的直角顶点放在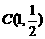 处,两直角边分别与
处,两直角边分别与 轴平行,纸板的另两个顶点
轴平行,纸板的另两个顶点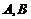 恰好是直线
恰好是直线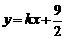 与双曲线
与双曲线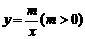 的交点.
的交点.
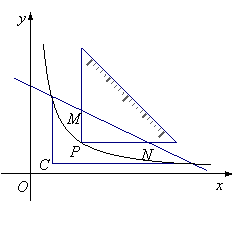 (1)求
(1)求 和
和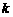 的值;
的值;
(2)设双曲线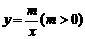 在
在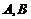 之间的部分为
之间的部分为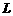 ,让一把三角尺的直角顶点
,让一把三角尺的直角顶点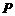 在
在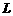 上
上
滑动,两直角边始终与坐标轴平行,且与线段 交于
交于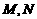 两点,请探究是否存在点
两点,请探究是否存在点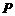 使得
使得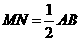 ,写出你的探究过程和结论.
,写出你的探究过程和结论.
知识点:
解:(1)∵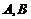 在双曲线
在双曲线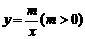 上,
上, ∥
∥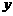 轴,
轴,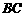 ∥
∥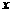 轴,
轴,
∴A,B的坐标分别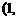
 ,
,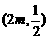 .
.
又点A,B在直线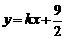 上,∴
上,∴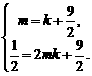
解得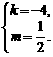 或
或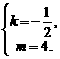
当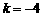 且
且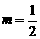 时,点A,B的坐标都是
时,点A,B的坐标都是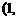
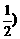 ,不合题意,应舍去;
,不合题意,应舍去;
当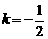 且
且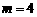 时,点A,B的坐标分别为
时,点A,B的坐标分别为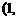
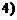 ,
,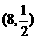 ,符合题意.
,符合题意.
∴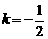 且
且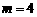 .
.
(2)假设存在点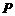 使得
使得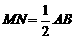 .
.
∵
 ∥
∥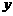 轴,
轴,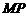 ∥
∥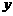 轴,∴
轴,∴ ∥
∥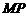 ,
,
∴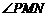
 ,∴Rt
,∴Rt ∽Rt
∽Rt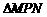 ,∴
,∴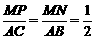 ,
,
设点P坐标为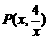 (1<x<8=,则M点坐标为
(1<x<8=,则M点坐标为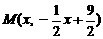 ,
,
∴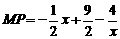 .又
.又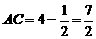 ,
,
∴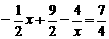 ,即
,即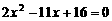 (※)
(※)
∵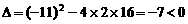 .∴方程(※)无实数根.
.∴方程(※)无实数根.
所以不存在点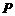 使得
使得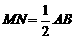 .
.
练习二
⑴方案①:把它折成横截面为直角三角形的水槽(如图1).
若∠ACB=90°,设AC=x厘米,该水槽的横截面面积为y厘米2,请你写出y关于x的函数关系式(不必写出x的取值范围),并求出当x取何值时,y的值最大,最大值又是多少?
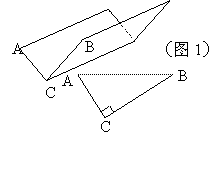
方案②:把它折成横截面为等腰梯形的水槽(如图2).
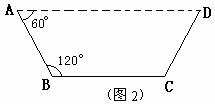 若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小.
若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小.
⑵假如你是该兴趣小组中的成员,请你再提供两种方案,使你所设计的水槽的横截面面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).
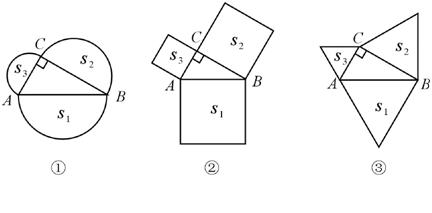
3(绵阳)如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3 .
(1) 如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(不必证明)
(2) 如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明;
(3) 若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1、S2、S3表示,为使S1、S2、S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件?证明你的结论;
(4) 类比(1)、(2)、(3)的结论,请你总结出一个更具一般意义的结论 .
4.(江苏)取一张矩形的纸片进行折叠,具体操作过程如下:
第一步:先把矩形ABCD对折,折痕为MN,如图(1);
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为 ,得Rt△A
,得Rt△A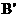 E,如图(2);
E,如图(2);
第三步:沿EB`线折叠得折痕EF,如图(3)。
利用展开图(4)探究:
(1)△AEF是什么三角形?
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由。
3、存 在 性 探 究 题
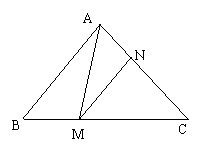 例1、如图,在△ABC中,BC=6,AC=
例1、如图,在△ABC中,BC=6,AC=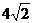 ,∠ACB=45°,在BC边上有一动点M,过M作MN∥AB,与AC交于点N,连结AM,设BM
,∠ACB=45°,在BC边上有一动点M,过M作MN∥AB,与AC交于点N,连结AM,设BM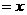
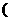 0<
0<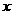 <6
<6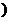 ,△AMN的面积为
,△AMN的面积为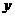 。(1)求
。(1)求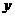 与
与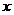 的函数关系式;
的函数关系式;
(2)是否存在这样的点M,使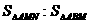 =2:3?
=2:3?
若存在则求之,否则说明理由。
例2、已知:如图,在平面直角坐标系中,点C在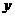 轴上,以C为圆心,4cm为半径的圆与
轴上,以C为圆心,4cm为半径的圆与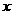 轴相交于点A、B,与
轴相交于点A、B,与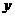 轴相交于D、E,且
轴相交于D、E,且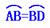 。点P是⊙C上一动点(P点与A、B点不重合)。连结BP、AP。
。点P是⊙C上一动点(P点与A、B点不重合)。连结BP、AP。
(1)求∠BPA的度数;
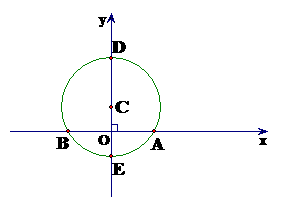 (2)若过点P的⊙C的切线交
(2)若过点P的⊙C的切线交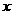 轴于点G,是否存在点P,使△APB与以A、G、P为顶点的三角形相似?
轴于点G,是否存在点P,使△APB与以A、G、P为顶点的三角形相似?
若存在,求出点P的坐标;若不存在,说明理由。
例3、(本小题满分8分)
探索下列问题:
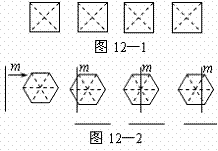
(1)在图12-1给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
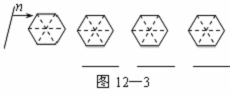
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2.
①请你在图12-2中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接);
②请你在图12-3中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).
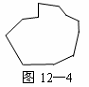
 (3)是否存在一条直线,将一个任意的平面图形(如图12-4)分割成面积相等的两部分,请简略说出理由.
(3)是否存在一条直线,将一个任意的平面图形(如图12-4)分割成面积相等的两部分,请简略说出理由.

2、条 件 探 究 题
条件探究题,一般是由给定的结论反过来探究命题成立应具备的条件。
 例1、已知:已知Rt△ABC中,∠C=90°,∠B的正切值是
例1、已知:已知Rt△ABC中,∠C=90°,∠B的正切值是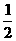 ,AC=3,点P为直线AC上的一点,当CP为何值时,
,AC=3,点P为直线AC上的一点,当CP为何值时,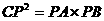 ?
?
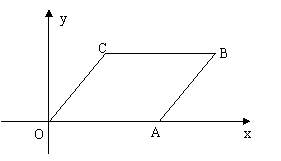 例2、已知:四边形ABCD是平行四边形,点A的坐标为(12,0),点C的坐标为(6,8),直线
例2、已知:四边形ABCD是平行四边形,点A的坐标为(12,0),点C的坐标为(6,8),直线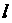 :
: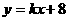 与
与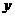 轴相交于点D。(1)当
轴相交于点D。(1)当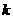 为何值时,直线
为何值时,直线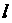 恰好平分平行四边形ABCD的面积?(2)若直线
恰好平分平行四边形ABCD的面积?(2)若直线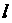 与线段CO、AO分别相交于点P、Q,
与线段CO、AO分别相交于点P、Q,
则当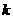 为何值时,△OPQ是等腰三角形?
为何值时,△OPQ是等腰三角形?
1、结 论 探 究 题
结论探究题,一般是由给定的已知条件探求相应的结论,解题时往往要求充分利用条件进行大胆而合理的猜想,发现规律,得出结论。
例1、有若干个数,第1个数记为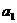 ,第2个数记为
,第2个数记为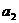 ,第3个数记为
,第3个数记为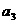 ,……,第
,……,第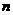 个数记为
个数记为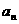 ,若
,若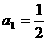 ,从第2个数起,每个数都等于“1与它前面的那个数的差的倒数”。
,从第2个数起,每个数都等于“1与它前面的那个数的差的倒数”。
(1)试计算: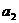 = ,
= ,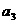 = ,
= ,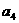 = ;
= ;
(2)根据以上计算结果,请你写出:
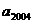 = ,
= ,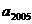 = 。
= 。
例2、水葫芦是一种水生飘浮植物,有着惊人的繁殖能力。据报现已造成某些流域河道堵塞,水质污染等严重后果。据研究表明:适量的水葫芦生长对水质的净化是有利的,关键是科学管理和转化利用。若在适宜条件下,1株水葫芦每5天就能新繁殖1株(不考虑植株死亡、被打捞等其它因素)。
(1)假设江面上现有一株水葫芦,填写下表:
|
第几天 |
5 |
10 |
15 |
… |
50 |
… |
5n |
|
总株数 |
2 |
4 |
|
|
|
|
|
(2)假设某流域内水葫芦维持在约33万株以内对净化水质有益。若现有10株水葫芦,请你尝试利用计算器进行估算探究,照上述生长速度,多少天时水葫芦约有33万株?此后就必须开始定期打捞处理水葫芦。(要求写出必要的尝试、估算过程!)
例3、如图,“取正方形各边的中点,并把相对的两个中点相连,这样把一个大正方形分成了四个小正方形”,我们称之为第1次操作。(1)请继续在图中按以上操作对右上角的正方形进行分割,我们称之为第2次操作。(2)继续按第1次操作的方法进行第3次、第4次分割,并把分割后图中小正方形的个数填入下表:(以后每次操作都对右上角正方形进行分割)
操作次数(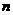 ) ) |
1 |
2 |
3 |
4 |
5 |
…… |
小正方形个数(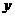 ) ) |
4 |
|
|
|
|
…… |
(3)进行第100次操作后,图中小正方形的个数是 。
 (4)能否当进行到某次操作后,使图中的小正方形
(4)能否当进行到某次操作后,使图中的小正方形
的个数为2004?若能,请求出操作的次数;
若不能,请说明理由。
 例4.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形。设格点多边形的面积为S,它各边上格点的个数和为
例4.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形。设格点多边形的面积为S,它各边上格点的个数和为 。
。
(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与 之间的关系式。
之间的关系式。
答:S= 。
|
多边形的序号 |
① |
② |
③ |
④ |
… |
|
多边形的面积S |
2 |
2.5 |
3 |
4 |
… |
各边上格点的个数和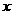 |
4 |
5 |
6 |
8 |
… |
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2格点。此时所画的各个多边形的面积S与它各边上格点的个数和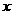 之间的关系式是:S=
。
之间的关系式是:S=
。
(3)请你继续探索,当格点多边形内部有且只有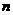 个格点时,猜想S与
个格点时,猜想S与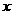 有怎样的关系?答:S=
。
有怎样的关系?答:S=
。
15. 已知抛物线y=x2+(2n-1)x+n2-1(n为常数)
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上的一个动点,它位于x轴下方,且在对称轴左侧,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C;
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由。
14. 下列各图是由小三角形拼凑而成的图形。
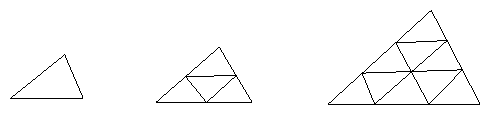
(1) (2) (3)
(1)请观察每一个图形中小三角形的个数,并完成下表:
|
层数n |
1 |
2 |
3 |
4 |
5 |
… |
|
小三角形的总数m |
|
|
|
|
|
… |
(2)根据上表中的数据,把n作为横坐标,把小三角形的总数m作为纵坐标,在平面直角坐标系中描出相应的各点(n,m)其中1≤n≤5;
(3)请你猜一猜,上述各点会在某一函数图象上吗?如果在某一函数的图象上,请写出该函数的表达式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com