
题目列表(包括答案和解析)
4. 如图2,已知∠1=∠2,若再增加一个条件就能使结论“AB·DE=AD·BC”成立,则这个条件可以是 。
3. 在△ABC和△ADC中,下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC将其中的两个论断作为条件,另一个论断作为结论写出一个真命题是 。
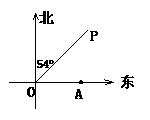
2. 如图1,某校为扩大高中招生,正在施工增盖教学楼,一推土机沿北偏东54°方向的OP工地线来回推土,它的噪声对位于O点正东方向200米处的一教室A已造成影响,当推土机的距O点 米处时,推土机的噪声对教室A影响最大。

(1) (2) (3)
1. 在四边形ABCD中,已知AB//CD,请补充条件 (写一个即可),使得四边形ABCD为平行四边形;若ABCD是平行四边形,请补充条件 (写一个即可),使四边形ABCD为菱形。
5、(2005年泰州)图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
(1)操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于F(图2);
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论.(4分)
(2)操作:将图2中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图3);
探究:设△PQR移动的时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
(3)操作:图1中△C′D′E′固定,将△ABC移动,使顶点C落在C′E′的中点,边BC交D′E′于点M,边AC交D′C′于点N,设∠AC C′=α(30°<α<90°=(图4);
 探究:在图4中,线段C′N·E′M的值是否随α的变化而变化?如果没有变化,请你求出C′N·E′M的值,如果有变化,请你说明理由.
探究:在图4中,线段C′N·E′M的值是否随α的变化而变化?如果没有变化,请你求出C′N·E′M的值,如果有变化,请你说明理由.
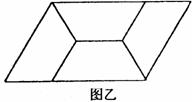
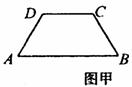
4、(2005年枣庄)如图甲,四边形ABCD是等腰梯形,AB∥DC.由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
(1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
(3)现有图甲中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图.
3、(2005年潜江、仙桃、江汉油田)我们做一个拼图游戏:用等腰直角三角形拼正方形。请按下面规则与程序操作:
第一次:将两个全等的等腰直角三角形拼成一个正方形;

 第二次:在前一个正方形的四条边上再拼上四个全等的等腰直角三角形(等腰直角三角形的斜边与正方形的边长相等),形成一个新的正方形;
第二次:在前一个正方形的四条边上再拼上四个全等的等腰直角三角形(等腰直角三角形的斜边与正方形的边长相等),形成一个新的正方形;
以后每次都重复第二次的操作-------
(1)请你在第一次拼成的正方形的基础上,画出第二次和第三次拼成的正方形图形;
(2)若第一次拼成的正方形的边长为a,请你根据操作过程中的观察与思考填写下表:
|
操作次数(n) |
1 |
2 |
3 |
4 |
--- |
n |
|
每次拼成的正方形面积(s) |
a2 |
|
|
|
--- |
|
2、(2005年河北)操作示例:
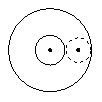
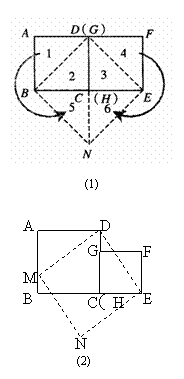 对于边长为a的两个正方形ABCD和EFGH,按图1所示的方式摆放,在沿虚线BD,EG剪开后,可以按图中所示的移动方式拼接为图1中的四边形BNED。
对于边长为a的两个正方形ABCD和EFGH,按图1所示的方式摆放,在沿虚线BD,EG剪开后,可以按图中所示的移动方式拼接为图1中的四边形BNED。
从拼接的过程容易得到结论:
①四边形BNED是正方形;
②S正方形ABCD+S正方形EFGH=S正方形BNED。
实践与探究
(1)对于边长分别为a,b(a>b)的两个正方形ABCD和EFGH,按图2所示的方式摆放,连接DE,过点D作DM⊥DE,交AB于点M,过点M作MN⊥DM,过点E作EN⊥DE,MN与EN相交于点N。
①证明四边形MNED是正方形,并用含a,b的代数式表示正方形MNED的面积;
②在图11-2中,将正方形ABCD和正方形EFGH沿虚线剪开后,能够拼接为正方形MNED,请简略说明你的拼接方法(类比图1,用数字表示对应的图形)。
(2)对于n(n是大于2的自然数)个任意的正方形,能否通过若干次拼接,将其拼接成为一个正方形?请简要说明你的理由。
1、已知:直线a∥b,P、Q是直线a上的两点,M、N是直线b上两点。
(1)如图①,线段PM、QN夹在平行直线a和b之间,四边形PMNQ为等腰梯形,其两腰PM=QN。
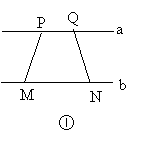 请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a和b之间的两条线段相等。
请你参照图①,在图②中画出异于图①的一种图形,使夹在平行直线a和b之间的两条线段相等。
(2)我们继续探究,发现用两条平行直线a、b去截一些我们学过的图形,会有两条“曲线段相等”(曲线上两点和它们之间的部分叫做“曲线段”。把经过全等变换后能重合的两条曲线段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在平行直线a和b之间的两条曲线段相等。
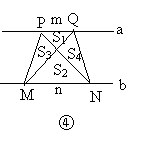
(3)如图④,若梯形PMNQ是一块绿化地,梯形的上底PQ=m,下底MN=n,且m<n。现计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里,使得价格相同的花草不相邻。为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由。
4、(2005深圳南山区).如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交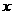 轴于D点,过点D作DF⊥AE于点F.
轴于D点,过点D作DF⊥AE于点F.
(1) 求OA、OC的长;
(2)求证:DF为⊙O′的切线;
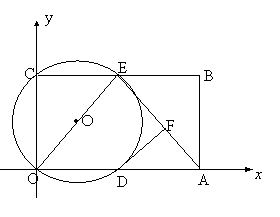 (3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
(3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
能力训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com