
题目列表(包括答案和解析)
3、在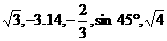 中,无理数的个数是_______
中,无理数的个数是_______
2、在实数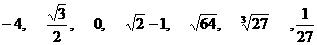 中,共有_______个无理数
中,共有_______个无理数
1、把下列各数填入相应的集合内:
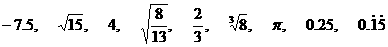
有理数集{ },无理数集{ }
正实数集{ }
3、______________________叫做无理数。一般说来,凡开方开不尽的数是无理数,但要注意,用根号形式表示的数并不都是无理数(如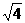 ),也不是所有的无理数都可以写成根号的形式(如
),也不是所有的无理数都可以写成根号的形式(如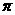 )。
)。
[典型考题]
2、实数和数轴上的点是___________对应的,每一个实数都可以用数轴上的________来表示,反过来,数轴上的点都表示一个________。
1、实数的分类:有理数,无理数。
21.我国著名数学家华罗庚说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
数形结合的基本思想,就是在研究问题的过程中,注意把数形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整数.
对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.
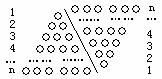
如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为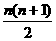 ,即1,2,3,…,n=
,即1,2,3,…,n=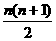 .
.
(1)依照上述数形结合的思想方法.设计相关图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)
(2)试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)
20.已知A=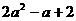 ,B=2,C=
,B=2,C=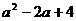 ,其中
,其中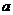 >1.
>1.
(1)求证:A-B>0;
(2)试比较A.B.C三者之间的大小关系,并说明理由.
19.老师在黑板上写出三个算式: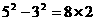 ,
,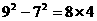 ,
,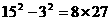 ,王华接着又写了两个具有同样规律的算式:
,王华接着又写了两个具有同样规律的算式: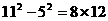 ,
,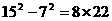 ,……
,……
(1)请你再写出两个(不同于上面算式)具有上述规律的算式;
(2)用文字写出反映上述算式的规律;
(3)证明这个规律的正确性.
18.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数” .如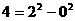 ,
,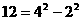 ,
,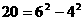 ,因此4,12,20这三个数都是神秘数.
,因此4,12,20这三个数都是神秘数.
(1)28和2012这两个数是神秘数吗?
(2)设两个连续偶数为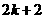 和
和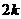 (其中
(其中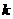 取非负整数).由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
取非负整数).由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com