
题目列表(包括答案和解析)
(一)选择题
1、计算机上,为了让使用者清楚、直观地看出磁盘“已用空间”与“可用空间”占“整个磁盘空间”的百分比,使用的统计图是( )
A 条形统计图 B 折线统计图
C 扇形统计图 D 条形统计图或折线统计图
2、 小明把自己一周的支出情况,用右图所示的统计图来表示,下面说法正确的是 ( )
小明把自己一周的支出情况,用右图所示的统计图来表示,下面说法正确的是 ( )
A.从图中可以直接看出具体消费数额
B.从图中可以直接看出总消费数额
C.从图中可以直接看出各项消费数额占总消费额的百分比
D.从图中可以直接看出各项消费数额在一周中的具体变化情况3、下列事件是随机事件的是( )
(A)两个奇数之和为偶数, (B)三条线段围成一个三角形
(C)广州市在八月份下了雪, (D)太阳从东方升起。
4、下列调查方式合适的是 ( )
A.为了了解炮弹的杀伤力,采用普查的方式
B.为了了解全国中学生的睡眠状况,采用普查的方式
C.为了了解人们保护水资源的意识,采用抽样调查的方式
D.对载人航天器“神舟六号”零部件的检查,采用抽样调查的方式
5、下列事件:①检查生产流水线上的一个产品,是合格品.②两直线平行,内错角相等.③三条线段组成一个三角形.④一只口袋内装有4只红球6只黄球,从中摸出2只黑球.其中属于确定事件的为( )
A、②③ B、②④ C、③④ D、①③
6、甲、乙、丙三人随意排成一列拍照,甲恰好排在中间的概率( )
(A) (B) (C) (D)以上都不对
7、从1,2,3,4,5的5个数中任取2个,它们的和是偶数的概率是( )
(A) (B) (C) (D)以上都不对
6、统计和概率的知识和观念在实际中的应用。能解决一些简单的实际问题。
例15:下列抽样调查:
①某环保网站就“是否支持使用可回收塑料购物袋”进行网上调查;
②某电脑生产商到当地一私立学校向学生调查学生电脑的定价接受程度;
③为检查过往车辆的超载情况,交警在公路上每隔十辆车检查一辆;
④为了解《中考指要》在学生复习用书中受欢迎的程度,随机抽取几个学校的初三年级中的几个班级作调查.
其中选取样本的方法合适的有:( )
A、1个 B、2个 C、3个 D、4个
例16:某农户在山上种脐橙果树44株,现进入第三年收获。收获时,先随机采摘5株果树上的脐橙,称得每株果树上脐橙重量如下(单位:kg):35,35,34,39,37。
⑴试估计这一年该农户脐膛橙的总产量约是多少?
⑵若市场上每千克脐橙售价5元,则该农户这一年卖脐橙的收入为多少?
⑶已知该农户第一年果树收入5500元,根据以上估算第二年、第三年卖脐橙收入的年平均增长率。
5、确定事件(分为必然事件、不可能事件)、不确定事件(称为随机事件或可能事件)、概率。并能用树状图和列表法计算概率;
例12:下列事件中,属于必然事件的是( )
A、明天我市下雨 B、抛一枚硬币,正面朝上
C、我走出校门,看到的第一辆汽车的牌照的末位数字是偶数
D、一口袋中装有2个红球和1个白球,从中摸出2个球,其中有红球
例13:用列表的方法求下列概率:已知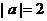 ,
,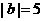 .求
.求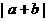 的值为7的概率.
的值为7的概率.
例14:画树状图或列表求下列的概率:袋中有红、黄、白色球各一个,它们除颜色外其余都相同,任取一个,放回后再任取一个.画树状图或列表求下列事件的概率.
(1)都是红色 (2)颜色相同 (3)没有白色
4、频数,频率,频率分布,常用的统计图表。
例9:第十中学教研组有25名教师,将他的年龄分成3组,在38-45岁组内有8名教师,那么这个小组的频率是( )
 (A)0.12 (B)0.38
(C)0.32 (D)3.12
(A)0.12 (B)0.38
(C)0.32 (D)3.12
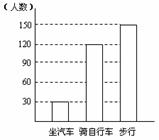
例10:如图是某校初一年学生到校方式的条形统计图,根据图形可得出步行人数占总人数的( )
A.60%; B.50%;
C.30%; D.20%.
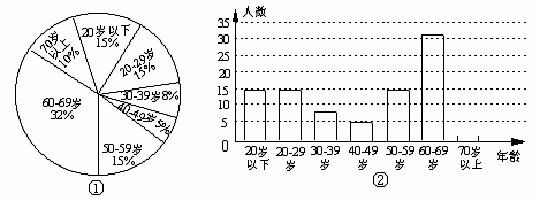 例11:在市政府举办的“迎奥运登山活动”中,参加白云山景区登山活动的市民约有12000人,为统计参加活动人员的年龄情况,我们从中随机抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图(部分)如下:
例11:在市政府举办的“迎奥运登山活动”中,参加白云山景区登山活动的市民约有12000人,为统计参加活动人员的年龄情况,我们从中随机抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图(部分)如下:
(1)根据图①提供的信息补全图②;
(2)参加登山活动的12000余名市民中,哪个年龄段的人数最多?
(3)根据统计图提供的信息,谈谈自己的感想.(不超过30字)
3、方差,标准差与极差。方差:顾名思义是“差的平方”,因有多个“差的平方”,所以要求平均数,弄清是“数据与平均数差的平方的平均数”,标准差是它的算术平方根。 会用计算器计算标准差与方差。
例6:数据90,91,92,93的标准差是( )
(A) (B) (C) (D)
 例7:甲、乙两人各射靶5次,已知甲所中环数是8、7、9、7、9,乙所中的环数的平均数x=8,方差S2乙=0.4,那么,对甲、乙的射击成绩的正确判断是( )
例7:甲、乙两人各射靶5次,已知甲所中环数是8、7、9、7、9,乙所中的环数的平均数x=8,方差S2乙=0.4,那么,对甲、乙的射击成绩的正确判断是( )
(A)甲的射击成绩较稳定 (B)乙的射击成绩较稳定
(C)甲、乙的射击成绩同样稳定 (D)甲、乙的射击成绩无法比较
例8:一个样本中,数据15和13各有4个,数据14有2个,求这个样本的平均数、方差、标准差和极差(标准差保留两个有效数字)
2、中位数,众数,平均数,加权平均数,注意区分这些概念。
相同点:都是为了描述一组数据的集中趋势的。
不同点:中位数--中间位置上的数据(当然要先按大小排列)
众数--出现的次数多的数据。
例3:某校篮球代表队中,5名队员的身高如下(单位:厘米):185,178,184,183,180,则这些队员的平均身高为( )
(A)183 (B)182 (C)181 (D)180
例4:已知一组数据为3,12,4,x,9,5,6,7,8的平均数为7,则x=
例5:某班第二组男生参加体育测试,引体向上成绩(单位:个)如下:
6 9 11 13 11 7 10 8 12
这组男生成绩的众数是____________,中位数是_________。
1、总体,个体,样本和样本容量。注意“考查对象”是所要研究的数据。
例1:为了了解某地区初一年级7000名学生的体重情况,从中抽取了500名学生的体重,就这个问题来说,下面说法中正确的是( )
(A)7000名学生是总体 (B)每个学生是个体
(C)500名学生是所抽取的一个样本 (D)样本容量是500
例2:某市今年有9068名初中毕业生参加升学考试,从中抽出300名考生的成绩进行分析。在这个问题中,总体是__________________________;个体是___ ________;样本是_______________________;样本容量是__________.
(二)点P的横、纵坐标都有数字1,2,3,4,5,6六种选择,所以构成点P的坐标
共有6×6 = 36种情况.
(1)移动0(即不移动)时,为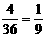 .
.
(2)先下移1个单位,后左移0.1个单位时,为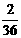 ,
,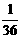 ,即
,即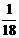 ,
,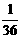 .
.
(3) 先下移1个单位,后右移1,2,3个单位时,为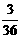 ,
,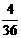 ,
,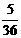 ,即
,即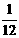 ,
,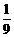 ,
,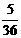 .
.
(4)先左移1个单位,后下移0.1个单位时,为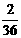 ,
,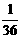 ,即
,即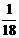 ,
,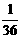 .
.
(5) 先左移1个单位,后上移1,2,3个单位时,为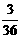 ,
,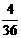 ,
,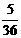 ,即
,即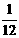 ,
,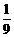 ,
,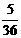 .
.
(6)上移1,2,3个单位时,为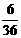 ,
,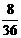 ,
,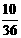 ,即
,即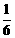 ,
,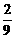 ,
,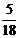 .
.
(7)右移1,2,3个单位时,为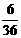 ,
,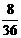 ,
,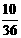 ,即
,即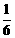 ,
,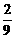 ,
,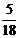 .
.
(8)先上移1个单位,后右移1,2,3个单位时,为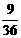 ,
,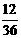 ,
,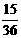 ,即
,即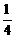 ,
,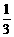 ,
,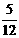 .
.
(9)先上移2个单位,后右移1,2,3个单位时,为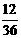 ,
,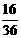 ,
,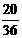 ,即
,即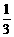 ,
,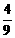 ,
,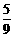 .
.
(10)先上移3个单位,后右移1,2,3个单位时,为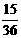 ,
,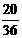 ,
,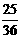 ,即
,即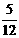 ,
,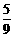 ,
,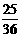 .
.
(11)正方形下移或左移超过1个单位时,点P落在正方形ABCD面上的概率为0.在此点P落在正方形ABCD面上的概率(不同)为:
0,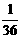 ,
,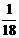 ,
,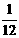 ,
,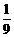 ,
,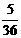 ,
,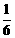 ,
,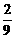 ,
,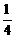 ,
,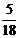 ,
,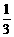 ,
,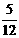 ,
,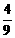 ,
,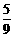 ,
,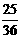 .
.
(二)若将(一)中所做实验用的“正四面体骰子”改为“各
面标有1 至6这六个数字中的一个的正方体骰子”,其余(实验
|
出点P落在正方形ABCD面上的概率.
[解](一)(1) 根据题意,点P的横坐标有数字1,2,3,4四种选择,点P的纵坐标也有数字1,2,3,4四种选择,所以构成点P的坐标共有4×4 = 16种情况.其中点P的(1,1),(1,2),(2,1),(2,2)四种情况将落在正方形ABCD面上,故所求的概率为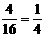 .
.
(2)因为要使点P落在正方形ABCD面上的概率为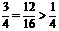 ,所以只能将正方
,所以只能将正方
形ABCD向上或向右整数个单位平移,且使点P落在正方形面上的数目为12.存
在满足题设要求的平移方式:先将正方形ABCD上移2个单位,后右移1个单位
(先右后上亦可);或先将正方形ABCD上移1个单位,后右移2个单位(先右后
上亦可).
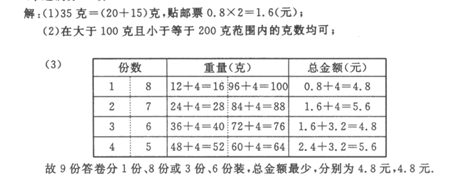
2 4.今年,苏州市政府的一项实事工程就是由政府投人1 000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
4.今年,苏州市政府的一项实事工程就是由政府投人1 000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
|
改造 情况 |
均不 改造 |
改造水龙头 |
改造马桶 |
||||
|
1个 |
2个 |
3个 |
4个 |
1个 |
2个 |
||
|
户数 |
20 |
31 |
28 |
21 |
12 |
69 |
2 |
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有_____户;
(2)改造后.一只水龙头一年大约可节省5吨水,一只马桶一年大约可节省15吨水.试估
计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中.既要改造水龙头又要改造马桶的家庭共有多少户?
解:(1) 1000;
(2) 抽样的120户家庭一年共可节约用水:
(1×31+2×28+×21+4×12)× 5+(1×69+2×2)×15=198×5+73×15=2085。
2085×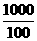 =20850(吨)。
=20850(吨)。
答:该社区一年共可节约用水20850吨。
(3) 设既要改造水龙头又要改造马桶的家庭共有x户,则只改造水龙头不改造马桶的家庭共有(92-x)户,只改造马桶不改造水龙头的家庭共有(71-x)户,
∴ x+(92-x)+(71一x)=100,
∴x=63(户)。
答:既要改造水龙头又要改造马桶的家庭共有63户.
25.(一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:
 抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中的一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点的点数作为直角坐标系中P点的坐标(第一次的点数作横坐标,第二次的点数作纵坐标).
抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中的一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点的点数作为直角坐标系中P点的坐标(第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内和边界,下同)
的概率;
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,
 使点P落在正方形ABCD面上的概率为
使点P落在正方形ABCD面上的概率为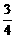 ?若存在,指出其中
?若存在,指出其中
的一种平移方式;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com