
题目列表(包括答案和解析)
在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母按规定要求涂抹在“机读答题卡”第1-8题的相应位置上.
1.一个数的倒数是-2,则这个数是 ( )
A.-2
B. 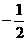 C.
2
D.
C.
2
D.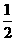
6.(基础教育课改实验区)某中学初三(1)班的全体同学在放假两周的时间内,在自主完成学习任务的同时,两周内全班每两个同学都通过一次电话,互相交流学习体会,共同提高.如果该班有56名同学,那么同学们之间共通了多少次电话?
为解决该问题,我们可把该班人数n与通电话次数s间的关系用下列模型来表示:
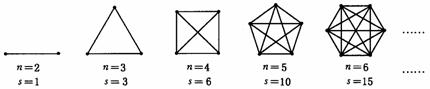
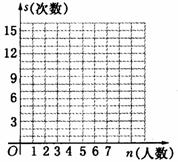 ⑴ 若把n作为点的横坐标,s作为纵坐标,根据上述模型中的数据,在给出的平面直角坐标系中,描出相应各点,并用平滑的曲线连接起来;
⑴ 若把n作为点的横坐标,s作为纵坐标,根据上述模型中的数据,在给出的平面直角坐标系中,描出相应各点,并用平滑的曲线连接起来;
⑵ 根据图中各点的排列规律,猜一猜上述各点会不会在某一函数的图像上?如果在,求出该函数的解析式;
⑶ 根据⑵中得出的函数关系式,求该班56名同学间共通了多少次电话。
5.(安徽) 下图中, 图(1)是一个扇形AOB,将其作如下划分:第一次划分: 如图(2)所示,以OA的一半OA1为半径画弧,再作∠AOB的平分线, 得到扇形的总数为6个, 分别为: 扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB1;第二次划分: 如图(3)所示, 在扇形C1OB1中, 按上述划分方式继续划分, 可以得到扇形的总数为11个;第三次划分: 如图(4)所示;……
依次划分下去.

图(1) 图(2)第一次划分 图(3)第二次划分 图(4)第三次划分
(1) 根据题意, 完成下表:
|
划分次数 |
扇形总个数 |
|
1 |
6 |
|
2 |
11 |
|
3 |
|
|
4 |
|
|
… |
… |
|
n |
|
(2) 根据上表, 请你判断按上述划分方式, 能否得到扇形的总数为2005个? 为什么?
4.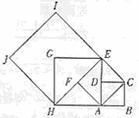 (广东) 设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去···。
(广东) 设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去···。
(1)记正方形ABCD的边长为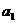 =1,依上述方法所作的正方形的边长依次为
=1,依上述方法所作的正方形的边长依次为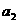 ,
,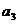 ,
,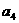 ,···,
,···,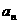 ,求出
,求出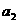 ,
,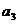 ,
,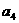 的值。
的值。
(2)根据以上规律写出第n个正方形的边长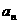 的表达式。
的表达式。
3.(扬州市)请选择一组你喜欢的a、b、c的值,使二次函数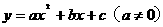 的图像同时满足下列条件:①开口向下,②当
的图像同时满足下列条件:①开口向下,②当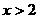 时,y随x的增大而减小;当
时,y随x的增大而减小;当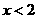 时,y随x的增大而增大.这样的二次函数的解析式可以是____________________.
时,y随x的增大而增大.这样的二次函数的解析式可以是____________________.
2.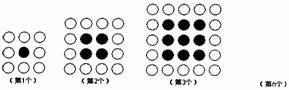 (茂名) 用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子 枚(用含有n的代数式表示)
(茂名) 用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子 枚(用含有n的代数式表示)
1.(丽水)下列是三种化合物的结构式及分子式,请按其规律,写出后一种化合物的分子式 .
6.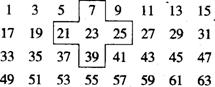 将连续的奇数1,3,5,7,9……排成如图所示数表:
将连续的奇数1,3,5,7,9……排成如图所示数表:
(1)十字框中的五个数的和与中间的数23有什么关系?
(2)设中间的数为a,用代数式表示十字框中的五个数之和.
(3)若将十字框上、下、左、右平移,可框住另外五个数,这五个数还有这种规律吗?
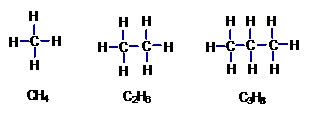 (4)十字框中的五个数之和能等于2010吗?若能,请写出这五个数.若不能,请说明理由.
(4)十字框中的五个数之和能等于2010吗?若能,请写出这五个数.若不能,请说明理由.
体验中考
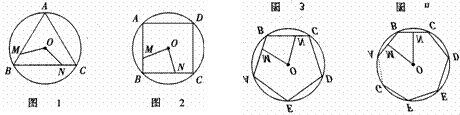
5.(大连) 如图1、2、3、…、n,M、N分别是⊙O的内接正三角形ABC,正方形ABCD、正五边形ABCDE、…、正n边形ABCD…的边AB、BC上的点,且BM=CN,连结OM、ON,
(1)图1中∠MON的度数是 ;
(2)图2中,∠MON的度数是_______,图3中∠MON的度数是________。
(3)试探索∠MON的度数与正多边形边数n的关系(直接写答案)
4.(南通市) 已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图所示).
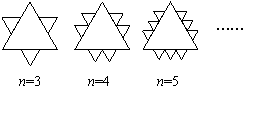 (1)当n = 5时,共向外作出了 个小等边
(1)当n = 5时,共向外作出了 个小等边
三角形,每个小等边三角形的面积为 ;
(2)当n = k时,共向外作出了 个
小等边三角形,这些小等边三角形的面积和
为 (用含k的式子表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com