
题目列表(包括答案和解析)
3.为了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班9名学生进行了调查,有关数据如下表:
|
每周做家务的时间(小时) |
0 |
1 |
2 |
3 |
4 |
|
人数(人) |
2 |
2 |
3 |
1 |
1 |
 则这9名学生每周做家务劳动的时间的众数及中位数分别是
则这9名学生每周做家务劳动的时间的众数及中位数分别是
A.3,2.5 B.1,2 C.3,3 D.2,2
2.根据北京移动公布的短信发送量显示,从大年三十到初六,7天内北京移动手机用户彩信发送总量超过了67,000,000条.将67000000用科学记数法表示应为
A.67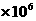 B. 6.7
B. 6.7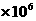 C.6.7
C.6.7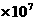 D.6.7
D.6.7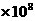
在下列各题的四个备选答案中,只有一个选项是正确的.用2B铅笔把“答题卡”上对应题目答案的相应字母涂黑.
1.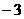 的相反数是
的相反数是
A.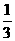 B.
B. 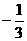 C.
C. 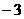 D. 3
D. 3
解:(1)解方程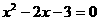 ,得
,得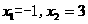 .………………1分
.………………1分
∴点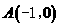 ,点
,点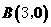 .
.
∴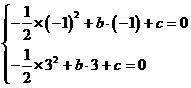
解,得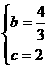
∴抛物线的解析式为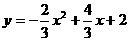 .·················································· 2分
.·················································· 2分
(2)∵抛物线与y轴交于点C.
∴点C的坐标为(0,2).
又点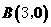 ,可求直线BC的解析式为
,可求直线BC的解析式为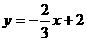 .
.
∵AD∥CB,∴设直线AD的解析式为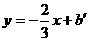 .
.
又点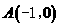 ,∴
,∴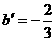 ,直线AD的解析式为
,直线AD的解析式为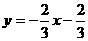 .
.
解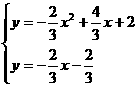 ,得
,得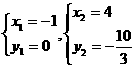 ,
,
∴点D的坐标为(4,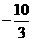 ).·········································································· 4分
).·········································································· 4分
过点D作DD’
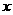 轴于D’, DD’=
轴于D’, DD’=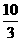 ,则又AB=4.
,则又AB=4.
∴四边形ACBD的面积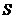 =
=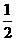 AB•OC+
AB•OC+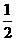 AB•DD’=
AB•DD’=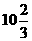 ······························ 5分
······························ 5分
(3)假设存在满足条件的点R,设直线l交y轴于点E(0,m),
∵点P不与点A、C重合,∴0< m <2,∵点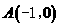 ,点
,点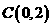 ,
,
∴可求直线AC的解析式为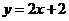 ,∴点
,∴点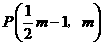 .
.
∵直线BC的解析式为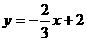 ,∴点
,∴点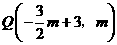 .
.
∴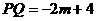 .在△PQR中,
.在△PQR中,
①当RQ为底时,过点P作PR1⊥x轴于点R1,则∠R1PQ=90°,PQ=PR1=m.
∴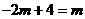 ,解得
,解得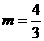 ,∴点
,∴点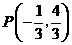 ,
,
∴点R1坐标为(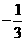 ,0).··········································································· 6分
,0).··········································································· 6分
②当RP为底时,过点Q作Q R2⊥x轴于点R2,
同理可求,点R2坐标为(1,0).································································ 7分
③当PQ为底时,取PQ中点S,过S作SR3⊥PQ交x轴于点R3,则PR3=QR3,∠PR3Q=90°.∴PQ=2R3S=2m.∴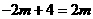 ,解,得
,解,得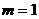 ,
,
∴点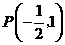 ,点
,点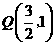 ,可求点R3坐标为(
,可求点R3坐标为(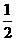 ,0). …………………8分
,0). …………………8分
经检验,点R1,点R2,点R3都满足条件.
 综上所述,存在满足条件的点R,它们分别是R1(
综上所述,存在满足条件的点R,它们分别是R1(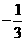 ,0),R2(1,0)和点R3(
,0),R2(1,0)和点R3(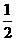 ,0).
,0).
24. 解:(1)∵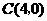 ,
,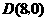 ,∴
,∴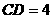 ,
,
∵矩形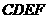 中,
中,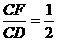 ,∴
,∴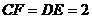 ,
,
∵点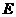 、
、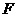 在第一象限,∴
在第一象限,∴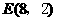 ,
,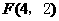 .………………………1分
.………………………1分
(2)由题意,可知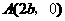 ,
,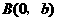 ,在Rt△ABO中,tan∠BAO=
,在Rt△ABO中,tan∠BAO=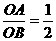 ,
,
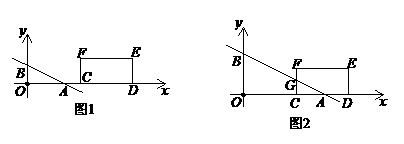
①当0<b≤2时,如图1,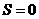 .……………………………………………2分
.……………………………………………2分
②当2<b≤4时,如图2,设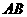 交
交 于
于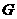 ,
,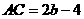 ,
,
在Rt△AGC中,∵tan∠BAO=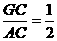 ,∴
,∴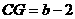 .
.
 ∴
∴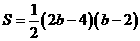 ,即
,即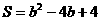 ,……………………………4分
,……………………………4分
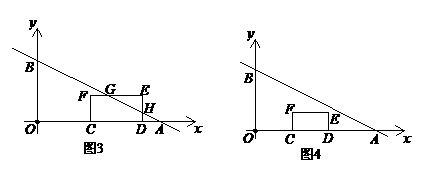
③当4<b≤6时,如图3,设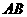 交
交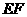 于
于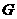 ,交
,交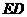 于
于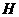 ,
,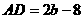 ,
,
在Rt△ADH中,∵tan∠BAO=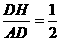 ,∴
,∴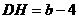 ,
,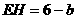 ,
,
在矩形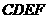 中,∵CD∥EF,∴∠EGH=∠BAO,
中,∵CD∥EF,∴∠EGH=∠BAO,
在Rt△EGH中,∵tan∠EGH=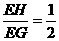 ,∴
,∴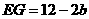 ,
,
∴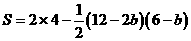 ,即
,即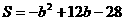 ,……………5分
,……………5分
④当b>6时,如图4,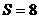 .………………………………………………6分
.………………………………………………6分
(3)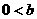 ≤
≤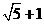 . ………………………………………………………7分
. ………………………………………………………7分
23.(1)①垂直,相等;………………………………………………………………………1分
②当点D在BC的延长线上时①的结论仍成立.…………………………………2分
由正方形ADEF得 AD=AF ,∠DAF=90º.
 ∵∠BAC=90º,∴∠DAF=∠BAC , ∴∠DAB=∠FAC,
∵∠BAC=90º,∴∠DAF=∠BAC , ∴∠DAB=∠FAC,
又AB=AC ,∴△DAB≌△FAC ,
∴CF=BD , ∠ACF=∠ABD.
∵∠BAC=90º, AB=AC ,
∴∠ABC=45º,∴∠ACF=45º,
∴∠BCF=∠ACB+∠ACF=90º.
即 CF⊥BD. ……………………………………………………………………5分
(2)当∠ACB=45º时,CF⊥BD(如图).……………………………………………6分
理由:过点A作AG⊥AC交CB或CB的延长线于点G,
则∠GAC=90º,
∵∠ACB=45°,∠AGC=90°-∠ACB=45°,
∴∠ACB=∠AGC,∴AC=AG,
∵点D在线段BC上,∴点D在线段GC上,
由(1)①可知CF⊥BD. …………………………………………………………7分
22.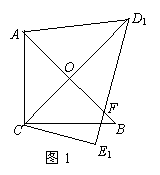 解:(1)如图1,由题意可知:∠BCE1=15°,
解:(1)如图1,由题意可知:∠BCE1=15°,
∵∠D1CE1=60°,
∴∠D1CB=∠D1CE1-∠D1CB=45°,
又∠ACB=90°,
∴∠ACD1=∠ACB-∠D1CB=45°.············ 1分
(2)由(1)知,∠ACD1=45°,
又∠CAB=45°,
∴∠AOD1=∠CAB+∠ACD1=45°∴OC⊥AB,
∵∠BAC=45°,∠ABC=90°-∠BAC=45°,
∴∠ABC=∠BAC,∴AC=BC,
∴OC=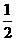 AB=OA=3,∴OD1=CD1-OC=4,
AB=OA=3,∴OD1=CD1-OC=4,
在Rt△AOD1中,∠5=90°,AD1=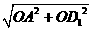 =5.·························· 3分
=5.·························· 3分
(3)点B在△D2CE2内部.············································································· 4分
理由如下:设BC(或延长线)交D2E2于点P,则∠PCE2=15°+30°=45°.
在Rt△PCE2中,可求CP=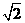
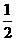 CE2=
CE2=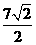 ,
,
在Rt△ABC中,可求BC=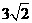 ,∵
,∵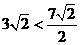 ,即BC <CP,………5分
,即BC <CP,………5分
∴点B在△D2CE2内部.
21.解:设该厂原来每天加工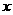 顶帐篷,则工作效率提高后每天加工1.5
顶帐篷,则工作效率提高后每天加工1.5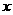 顶帐篷.······ 1分
顶帐篷.······ 1分
根据题意,得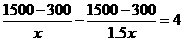 ,················································· 3分
,················································· 3分
解这个方程,得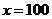 ,·············································································· 4分
,·············································································· 4分
经检验: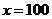 是原方程的解.
是原方程的解.
答:该厂原来每天加工100顶帐篷.······························································· 5分
20.解:(1)③,……………………1分
(2)图1补充完整, ……3分
(3)220. …………………5分
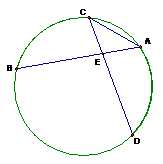
19.(1)证明:联结BO,……………………………1分
方法一:∵AB=AD,∴∠D=∠ABD,
∵AB=AO,
∴∠ABO=∠AOB,………………2分
又在△OBD中,∠D+∠DOB+∠ABO+∠ABD=180°,
∴∠OBD=90°,即BD⊥BO,
∴BD是⊙O的切线.········································································ 3分
方法二:∵AB=AO,BO=AO,∴AB=AO=BO,∴△ABO为等边三角形,
∴∠BAO=∠ABO=60°,
∵AB=AD,∴∠D=∠ABD,
又∠D+∠ABD=∠BAO=60°,∴∠ABD=30°, …………………2分
∴∠OBD=∠ABD+∠ABO=90°,即BD⊥BO,
∴BD是⊙O的切线. ……………………………………………………3分
方法三:∵ AB=AD=AO,∴点O、B、D在以OD为直径的⊙A上 …………2分
∴∠OBD=90°,即BD⊥BO,
∴BD是⊙O的切线. ……………………………………………………3分
(2)解:∵∠C=∠E,∠CAF=∠EBF,∴△ACF∽△BEF, …………………… 4分
∵AC是⊙O的直径,∴∠ABC=90°,
在Rt△BFA中,cos∠BFA=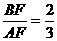 ,∴
,∴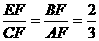 ,
,
 又∵CF=9,
又∵CF=9,
∴EF=6.…………………5分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com