
题目列表(包括答案和解析)
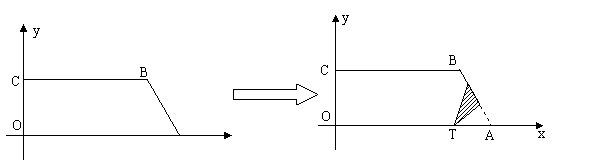
28.已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,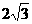 ),C(0,
),C(0,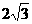 ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式,并写出t的取值范围;
(2)当纸片重叠部分的图形是四边形时,求t的取值范围;
(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由。(本题满分12分)

|
|
|
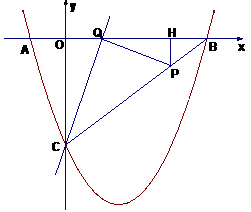
27.如图,已知抛物线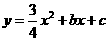 与坐标轴交于
与坐标轴交于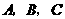 三点,点
三点,点 的横坐标为
的横坐标为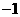 ,过点
,过点 的直线
的直线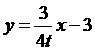 与
与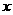 轴交于点
轴交于点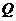 ,点
,点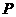 是线段
是线段 上的一个动点,过P作
上的一个动点,过P作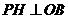 于点
于点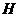 .若
.若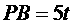 ,且
,且 .
.
(1) 则 ,B( , );
,B( , );
(2) 求点Q、P的坐标(用含 的式子表示)和线段
的式子表示)和线段 的长度(用含
的长度(用含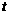 的式子表示);
的式子表示);
(3) 依据点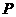 的变化,是否存在
的变化,是否存在 的值,使
的值,使 与
与 相似?若存在,求出所有
相似?若存在,求出所有 的值;若不存在,说明理由.(本题满分12分)
的值;若不存在,说明理由.(本题满分12分)
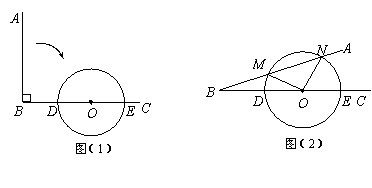
26. 如图(1),∠ABC=90°,O为射线BC上一点,OB = 4,以点O为圆心,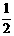 BO长为半径作⊙O交BC于点D、E.
BO长为半径作⊙O交BC于点D、E.
(1)当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切?请说明理由.
(2)若射线BA绕点B按顺时针方向旋转与⊙O相交于M、N两点(如图(2)),MN=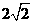 ,求的长.(本题满分10分)
,求的长.(本题满分10分)
25.在边长为1的正方形网格中,有形如帆船的图案①和半径为2的⊙P.
⑴将图案①进行平移,使A点平移到点E,画出平移后的图案;
⑵以点M为位似中心,在网格中将图案①放大2倍,画出放大后的图案,并在放大后的图案中标出线段AB的对应线段CD;
⑶在⑵所画的图案中,线段CD被⊙P所截得的弦长为________,该弦与其所对的弧围成的图形面积为__________________________ (结果保留根号)。(本题满分10分)

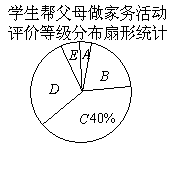
24.九年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成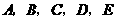 五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
学生帮父母做家务活动时间频数分布表
|
等级 |
帮助父母做家务时间(小时) |
 频数 频数 |
|
A |
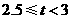 |
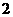 |
|
B |
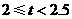 |
10 |
|
C |
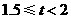 |
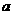 |
|
D |
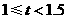 |
 |
|
E |
 |
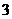 |
(1)求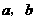 的值;
的值;
(2)根据频数分布表估算出该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.
(本题满分10分)
23. 如图,某人在山坡坡脚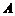 处测得电视塔尖点
处测得电视塔尖点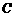 的仰角为
的仰角为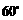 ,沿山坡向上走到
,沿山坡向上走到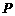 处再测得点
处再测得点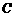 的仰角为
的仰角为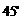 ,已知
,已知 米,山坡坡度
米,山坡坡度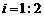 且
且 在同一条直线上.求电视塔
在同一条直线上.求电视塔 的高度以及此人所在位置
的高度以及此人所在位置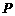 的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)(本题满分10分)
的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)(本题满分10分)
22.某公司有甲、乙两种品牌的激光打印机,其中甲品牌有A、B两种型号,乙品牌有C、D、E三种型号.某中学计划从甲、乙两种品牌中各选购一种型号的激光打印机. (1)利用树状图或列表法写出所有的选购方案; (2)如果各种型号的激光打印机被选购的可能性相同,那么C型号激光打印机被选购的概率是多少?(本题满分8分)
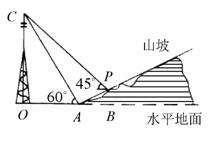
21. 如图,在Rt△ABC中,∠C=900,∠A=600,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC.
 (1)猜测AE与BE的数量关系,并说明理由.
(1)猜测AE与BE的数量关系,并说明理由.
(2)求证:四边形AEDF是菱形(本题满分8分)
20. (1)求不等式组 的整数解.(本小题4分)
的整数解.(本小题4分)
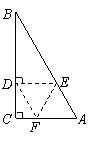
(2)解分式方程:
 (本小题4分)
(本小题4分)
19.(1)计算:2sin60°- +(
+(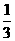 )-1+(-1)2009(本小题4分)
)-1+(-1)2009(本小题4分)
(2)先化简,再求值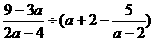 ,其中a满足
,其中a满足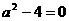 (本小题4分)
(本小题4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com