
题目列表(包括答案和解析)
22.解:(1)∵Rt△ABC绕点M旋转得△DEA,
∴△ABC≌△DEA,且AM=DM,BM=EM --------------------------------1分
∴∠DAE=∠C=90°,∠E=∠B=25°, -------------------------------------1分
∵AM=BM,∴DM=EM,即M为Rt△DEA斜边中点
∴MA=ME--------------------------------------------------------------------1分
∴∠BAE=∠E,∴∠BAE =25°-----------------------------------------2分
(2) ∵∠BAE=∠E,又∵∠E=∠B,∴∠BAE=∠B,∴AN=NB---------------1分
设CN=x,则AN=NB=3-x
在Rt△CAN中,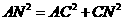 ,即
,即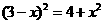 ---------------2分
---------------2分
解得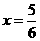 -----------------------------------------------------------------------------2分
-----------------------------------------------------------------------------2分
21.(本题10分)
(1) 证明:联结AC、AD----------------------------------------------------------------1分
∵点F是CD 的中点,且AF⊥CD,∴AC=AD---------------1分
∴∠ACD=∠ADC------------------------------------------------------1分
∵∠BCD=∠EDC, ∴∠ACB=∠ADE-------------------------1分
∵BC=DE,AC=AD
∴△ABC≌△AED, -------------------------------------------------------1分
∴AB=AE-------------------------------------------------------------------1分
(2) BE⊥AF,BE//CD,AF平分BE--------------------------------------1分,1分,2分
(注:写出一个得1分,写出两个得2分,写出三个得4分)
20.
解:设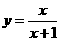 ,则原方程化为
,则原方程化为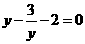 ------------------------------------1分
------------------------------------1分
则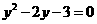 -------------------------------------------------------------------------2分
-------------------------------------------------------------------------2分
解得: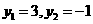 ------------------------------------------------------------------2分
------------------------------------------------------------------2分
当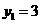 时,
时,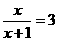 ,解得
,解得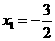 --------------------------------------------2分
--------------------------------------------2分
当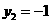 时,
时,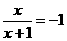 ,解得
,解得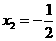 --------------------------------------------2分
--------------------------------------------2分
经检验,原方程的解是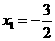 ,
,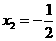 -----------------------------------------1分
-----------------------------------------1分
19.解:原式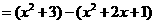 --------------------------------------------3分
--------------------------------------------3分
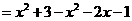 -------------------------------------------------1分
-------------------------------------------------1分
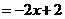 .--------------------------------------------------------------3分
.--------------------------------------------------------------3分
当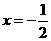 时,原式
时,原式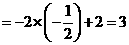 .--------------------------------------------3分
.--------------------------------------------3分
14.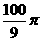 ;15.-2
;15.-2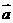 ;16.③;17.36;18.
;16.③;17.36;18.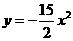
7.<;8. ;9.略;10.
;9.略;10.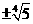 ;11.0<k<
;11.0<k<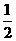 ;12.(0,-1);13.73;
;12.(0,-1);13.73;
1.D; 2.A; 3.C; 4.A; 5.B; 6.B
25.(本题14分)(第(1)小题4分,第(2)小题6分,第(3)小题4分)
如图,梯形ABCD中,AD//BC,CD⊥BC,已知AB=5,BC=6,cosB=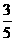 .点O为BC边上的动点,联结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,联结MN.
.点O为BC边上的动点,联结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,联结MN.
(1) 当BO=AD时,求BP的长;
(2) 点O运动的过程中,是否存在BP=MN的情况?若存在,请求出当BO为多长时BP=MN;若不存在,请说明理由;
(3) 在点O运动的过程中,以点C为圆心,CN为半径作⊙C,请直接写出当⊙C存在时,⊙O与⊙C的位置关系,以及相应的⊙C半径CN的取值范围。


2009年杨浦区初三数学模拟测试答案及评分标准2009.5
24.(本题12分)
已知一次函数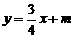 的图像分别交x轴、y轴于A、B两点(如图),且与反比例函数
的图像分别交x轴、y轴于A、B两点(如图),且与反比例函数
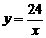 的图像在第一象限交于点C(4,n),CD⊥x轴于D。
的图像在第一象限交于点C(4,n),CD⊥x轴于D。
(1)求m、n的值;
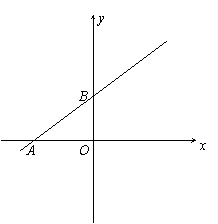 (2)如果点P在x轴上,并在点A与点D之间,点Q在线段AC上,且AP=CQ,那么当
(2)如果点P在x轴上,并在点A与点D之间,点Q在线段AC上,且AP=CQ,那么当
△APQ与△ADC相似时,求点Q的坐标.
23.(本题12分)
据悉,上海市发改委拟于今年4月27日举行居民用水价格调整听证会,届时将有两个方案提供听证。如图(1),射线OA、射线OB分别表示现行的、方案一的每户每月的用水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;方案二如图(2)表格所示,每月的每立方米用水价格由该月的用水量决定,且第一、二、三级的用水价格之比为1︰1.5︰2(精确到0.01元后).
(1) 写出现行的用水价是每立方米多少元?
(2) 求图(1)中m的值和射线OB所对应的函数解析式,并写出定义域;
(3) 若小明家某月的用水量是a立方米,请分别写出三种情况下(现行的、方案一和方案二)该月的水费b(用a的代数式表示);
(4) 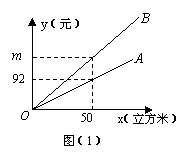 小明家最近10个月来的每月用水量的频数分布直方图如图(3)所示,估计小明会赞同采用哪个方案?请说明理由。
小明家最近10个月来的每月用水量的频数分布直方图如图(3)所示,估计小明会赞同采用哪个方案?请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com