
题目列表(包括答案和解析)
18.解:设AD’交BC于O,
方法一:
过点B作BE⊥AD’于E,
矩形ABCD中,
∵AD∥BC,AD=BC,
∠B=∠D=∠BAD=90°,
在Rt△ABC中,
∵tan∠BAC=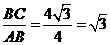 ,
,
∴∠BAC=60°,∴∠DAC=90°-∠BAC=30°,……………………………2分
∵将△ACD沿对角线AC向下翻折,得到△ACD’,
∴AD’=AD=BC=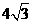 ,∠1=∠DAC=30°,
,∠1=∠DAC=30°,
∴∠4=∠BAC-∠1=30°,
又在Rt△ABE中,∠AEB=90°,∴BE=2, ……………………………………4分
∴AE=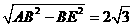 ,∴D’E=AD’-AE=
,∴D’E=AD’-AE=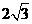 ,
,
∴AE=D’E,即BE垂直平分AD’,∴BD’=AB=4. ……………………………5分
方法二:
矩形ABCD中,∵AD∥BC,AD=BC,∠B=∠D=90°,∴∠ACB=∠DAC,
在Rt△ABC中,∵tan∠BAC=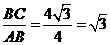 ,
,
∴∠BAC=60°,∴∠ACB=90°-∠BAC=30°,……………………………2分∵将△ACD沿对角线AC向下翻折,得到△ACD’,
∴AD=AD’=BC,∠1=∠DAC=∠ACB=30°,
∴OA=OC,
∴OD’=OB,∴∠2=∠3,
∵∠BOA=∠1+∠ACB=60°, ∠2+∠3=∠BOA,
∴∠2=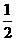 ∠BOA=30°,…………………………………………………………4分
∠BOA=30°,…………………………………………………………4分
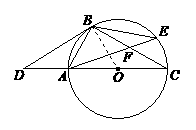 ∵∠4=∠BAC-∠1=30°,∴∠2=∠4,∴BD’=AB=4. …………………5分
∵∠4=∠BAC-∠1=30°,∴∠2=∠4,∴BD’=AB=4. …………………5分
17.解:(1)∵点A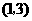 在反比例函数
在反比例函数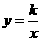 的图象上,∴
的图象上,∴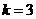 , …………………1分
, …………………1分
∴反比例函数的解析式为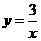 ,···························································· 2分
,···························································· 2分
∵点B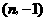 在反比例函数
在反比例函数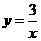 的图象上,
的图象上,
∴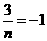 ,∴
,∴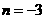 ,··········································································· 3分
,··········································································· 3分
∴点B的坐标为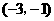 ,
,
∵点A、点B在一次函数 的图象上.
的图象上.
∴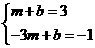 ,∴
,∴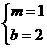
∴一次函数的解析式为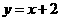 ······························································ 5分
······························································ 5分
16.解: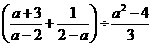
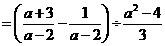
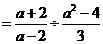 ………2分
………2分
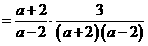
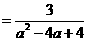 ······························································ 4分
······························································ 4分
∵ ∴
∴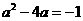
当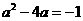 时, 原式
时, 原式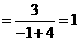 .·························································· 5分
.·························································· 5分
15.证明: ∵AB∥DE,∴∠B=∠DEF,··································································· 1分
∵BE=CF, ∴BE+CE=CF+CE,即BC=EF,····································· 2分
∵∠A=∠D,∴△ABC≌△DEF.···························································· 4分
∴∠ACB=∠F.························································································· 5分
13.解: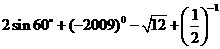 14.
14. 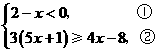
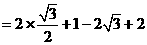 …………4分 解:解不等式①,得
…………4分 解:解不等式①,得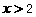 ;······ 2分
;······ 2分
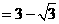 .………………………5分
解不等式②,得
.………………………5分
解不等式②,得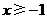 ;····· 4分
;····· 4分
在数轴上表示不等式①、②的解集,
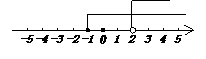
∴原不等式组的解集为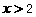 .··· 5分
.··· 5分
9.x≥1; 10.40; 11.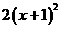 ; 12.
; 12.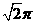 .
.
1.A; 2.D; 3.C; 4.B; 5.D; 6.B; 7.C; 8.A.
25.已知抛物线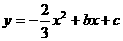 与x轴交于不同的两点
与x轴交于不同的两点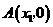 和
和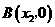 ,与y轴交于点C,且
,与y轴交于点C,且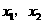 是方程
是方程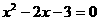 的两个根(
的两个根(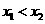 ).
).
(1)求抛物线的解析式;
(2)过点A作AD∥CB交抛物线于点D,求四边形ACBD的面积;
(3)如果P是线段AC上的一个动点(不与点A、C重合),过点P作平行于x轴的直线l交BC于点Q,那么在x轴上是否存在点R,使得△PQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.
数学试卷答案及评分参考
24.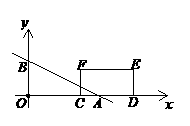 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线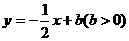 分别交
分别交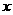 轴、
轴、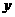 轴于
轴于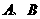 两点.点
两点.点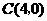 、
、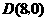 ,以
,以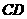 为一边在
为一边在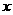 轴上方作矩形
轴上方作矩形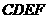 ,且
,且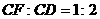 .设矩形
.设矩形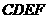 与
与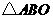 重叠部分的面积为
重叠部分的面积为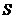 .
.
(1)求点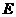 、
、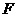 的坐标;
的坐标;
(2)当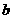 值由小到大变化时,求
值由小到大变化时,求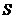 与
与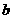 的函数关系式;
的函数关系式;
(3)若在直线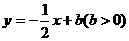 上存在点
上存在点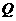 ,使
,使 等于
等于 ,请直接写出
,请直接写出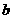 的取值范围.
的取值范围.
23.如图1,在 中,
中, 为锐角,点
为锐角,点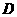 为射线
为射线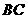 上一点,联结
上一点,联结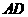 ,以
,以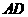 为一边且在
为一边且在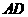 的右侧作正方形
的右侧作正方形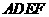 .
.
(1)如果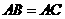 ,
,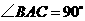 ,
,
①当点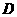 在线段
在线段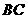 上时(与点
上时(与点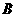 不重合),如图2,线段
不重合),如图2,线段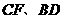 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段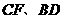 的数量关系为
;
的数量关系为
;
②当点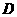 在线段
在线段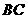 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;


(2)如果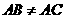 ,
,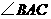 是锐角,点
是锐角,点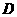 在线段
在线段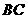 上,当
上,当 满足什么条件时,
满足什么条件时,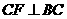 (点
(点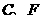 不重合),并说明理由.
不重合),并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com